大型圓環導軌平面度測量方法及在實際測量中的應用

江蘇新瑞重工科技有限公司 （常州 213166） 朱紅衛 尤敏志

大型回轉類零件圓環導軌平面度的測量方法較為復雜，在實際生產中大型圓環導軌也較為少見。本文就公司一臺LMV600車銑復合加工中心在生產制造中對其轉臺上圓環導軌平面度進行測量的整個過程進行分析與總結，希望能給讀者帶來一些啟發。

一、圓環導軌平面度測量的基本原理

這里我們的測量方法主要建立在電子水平儀基礎上，按水平儀測量方向將測量方法分為兩種類型，切向測量法和徑向測量法。

1.切向測量法的基本原理

切向測量法顧名思義是用水平儀對圓環導軌切向的水平傾角進行測量，從而得出圓環導軌的平面度。與直線導軌不同，圓環導軌測量所得到的數據做出的曲線不是一條直線，而是一條規律變化的曲線。

設想有一理想的標準圓導軌，它和物理水平面存在一微小的安裝傾角，如圖1所示。

圖中圓環導軌面與水平面間夾角為α，D為該圓環導軌的最高點，A點為水平儀測量位置，A′、D′分別為它們在水平面的投影。∠OAB=90°可以得到

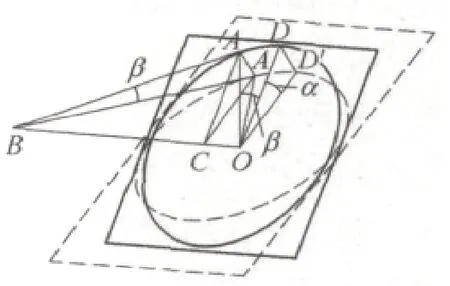
圖1

由上式可得

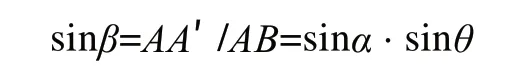
由于圓環導軌面與水平面間α夾角為非常小，β也就非常微小，所以

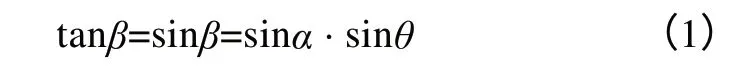
tanβ即為水平儀測量切向的讀數，sinα為一常數，由式（1）我們可以知道水平儀的讀數隨著其測量點的相位角呈正弦函數變化。于是我們可以通過計算得到圓環導軌上各點的切向斜率，與測量數據進行比較分析，我們即可得出每點偏差，從而測得圓環導軌的平面度。

2.徑向測量法

徑向測量法即是通過測量圓環導軌上各點到圓環中心方向上的傾斜角得到的數據來計算各點的偏差，從而達到測量平面度的目的。但是實際測量中因為隨著半徑的增大，使得測量的精度成倍的減少，所以這個方法測量的精度相對切向測量法要低得多。

二、數據的測量與處理方法

在上述兩種測量方法中，切向測量法不僅測量精度較高，而且所需測量工裝比較簡易，操作較為方便，因此我們選擇切向測量法作為本次測量的主要手段。下面來介紹切向測量法如何測量數據并進行處理。

1.測量方法

測量前我們需要將圓環導軌面調水平，保證其與物理水平面只有一個微小的夾角。將水平儀調零，保證其讀數精確可靠。

圖2

將圓周均分為n等分，如圖2所示，從任意位置A點開始將水平儀沿圓周切向按逆時針（或順時針）方向依次首尾相連放置進行連續測量讀數，并記錄數據。測量過程中，水平儀不可調頭，同時保證導軌面潔凈。

2.數據處理方法

相對較為簡易的測量步驟，測量數據的處理分析則顯得復雜得多，它也是整個測量過程中的關鍵部分。由于水平儀測得的是每一等分部分沿圓周切向的傾角，即使我們得到各點測量數據與理論值的偏差我們也無法直觀了解到各點凸出或凹入了多少，所以我們需要通過疊加法將各等分點間的傾角變成各點的相對高度值。

由式（1）我們知道傾角讀數

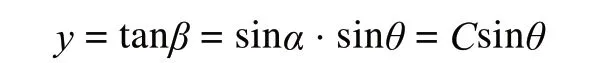
其中C=sinα為一常數，y呈正弦函數曲線。那么各點相對高度Y是不是也呈現為規律曲線呢？我們設起始相位角為的位置相對高度為0，則相位角為ψ的位置的相對高度Y為

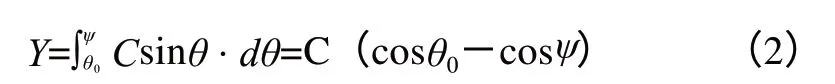
其中C和θ0均為常數，于是我們可以知道各點相對高度也是呈三角函數曲線的，將實際測得數據的累加值與理論計算值進行比較，得出各點的偏差作為依據對導軌面進行鏟刮。

下面以LMV600轉臺底座上圓環導軌外圈的一組測量數據為例，來說明如何對數據進行分析處理。附表即是一組測量所得數據。

測量數據

（1）將測量得到的數據逐一進行累加處理，得到曲線如圖3所示。

（2）連接曲線起點和終點，以連接兩點所得到的斜線為x軸對累加處理的曲線進行坐標轉換，即用累加曲線坐標減去斜線坐標得到新的曲線。如圖4、5所示。

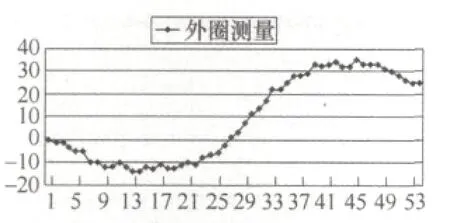
圖3

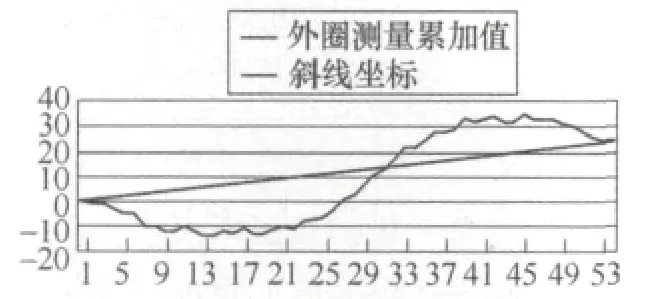
圖4

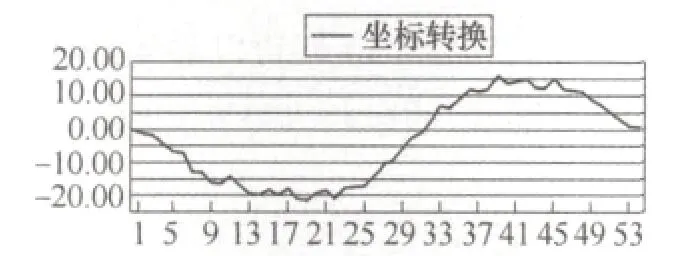
圖5

（3）將上一步得到的新曲線擬合成一條正弦函數曲線，這條正弦曲線的幅值為實測曲線最大值和最小值差值的一半，周期與實測曲線相同，我們移動該正弦函數曲線使其盡可能合理地靠攏實測曲線。如圖6所示。

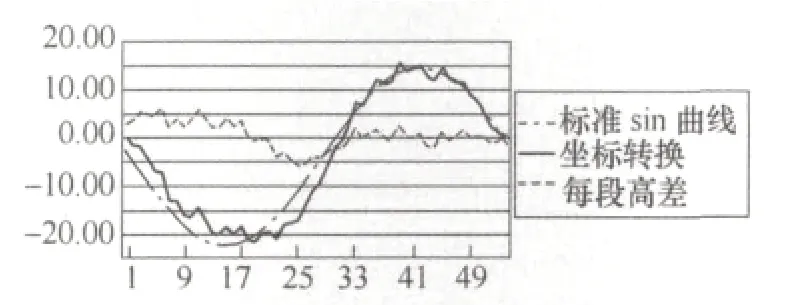
圖6

圖中兩條曲線不重合處就是導軌面的平面度，兩條曲線的差值即為各點相對理想圓環導軌面的偏差，實測曲線高出標準正弦曲線的部分為凸出的，而低于正弦曲線的部分則為凹下去的。

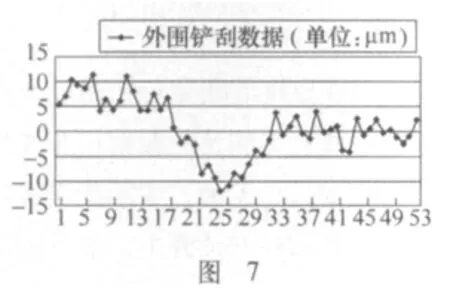
圖7為各測量點數據與理想值的差值。從圖中我們可以看到，最高凸出11μm、最低凹下去12μm，可以得到整個圓環導軌的平面度誤差為11+12=23（μm）。

三、通過Matlab進行數據處理

上述數據處理都是通過Excel來完成，但是在最后進行擬合曲線時顯然是存在一定問題，我們無法借助Excel很精確的將實測值擬合成正弦曲線。這里通過專業數據處理軟件的來解決這一問題，利用Matlab軟件可以很容易的完成任務。

1.Matlab數據處理程序

（1）創建一個目標函數

function diff=fit_sin（x，X，Y）

diff=x（1）+x（2）.*sin[X+x（3）]－Y；%創建目標函數供擬合用

（2）數據處理主程序 先將測量數據輸入，然后由程序對數據按照步驟進行預處理，再將處理后的數據利用非線性回歸擬合成目標函數，最后輸出函數圖像，程序實現如下：

DATA=input（'data='）；

n=input（'n='）； （輸入測量數據）

s=sum（DATA）；

t=0:1:n；

Change=t*s/n； （斜線坐標）

Y（1）=0；

i=2；

while i<=n+1

Y（i）=sum（DATA（1:i-1））-Change（i）； （累加值坐標轉換）

i=i+1；

end

X=0:2*pi/n:2*pi；

Y1=Y/10000；

X0=[1 1 1]'；

options=optimset（'Largescale'，'off'）；

x=lsqnonlin（@fit_sin，X0，[]，[]，options，X，Y1）； （擬合至目標函數）

Y_f i t=10000*x（1）+10000*x（2）.*s i n（X+x（3））；

Y_chan=Y-Y_fit；

Y_chan=Y_chan*200*0.01；（200為水平儀橋板長度，0.01為水平儀精度）

plot（X，Y，'r'，X，Y_fit，'b'，X，Y_chan，'k'）；（輸出曲線圖）

grid on

Y_chan

max（Y_chan）-min（Y_chan）（輸出平面度誤差）

2.結果分析與比較

將以上程序運行，輸入表1中圓環導軌外圈的測量數據，便得到如圖8曲線圖，圖中鏟刮量就是我們需要的計算值。

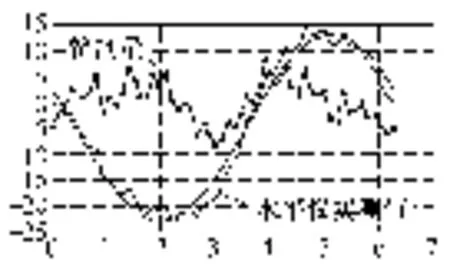
圖8

圖中每點的鏟刮量值為水平儀實測值與目標正弦函數的差值。由此圖我們可以得知該圓環導軌凸出最高8.08μm，凹陷最低8.56μm，所以該圓環導軌平面度誤差為16.64μm，精確擬合所得的結果竟比之前小了很多，利用軟件進行精確計算的重要性可見一斑。

四、用Minitab 非線性回歸的方法

從上述的分析過程來看，這是一個非線性回歸的過程，我們同樣也可以用Minitab 16.1 的這一功能來求精確解， 數據處理過程如下。

（1）新建一個工作表，如圖9所示，在第一列C1中輸入測量序號1～54（總的測量次數為54個點）。

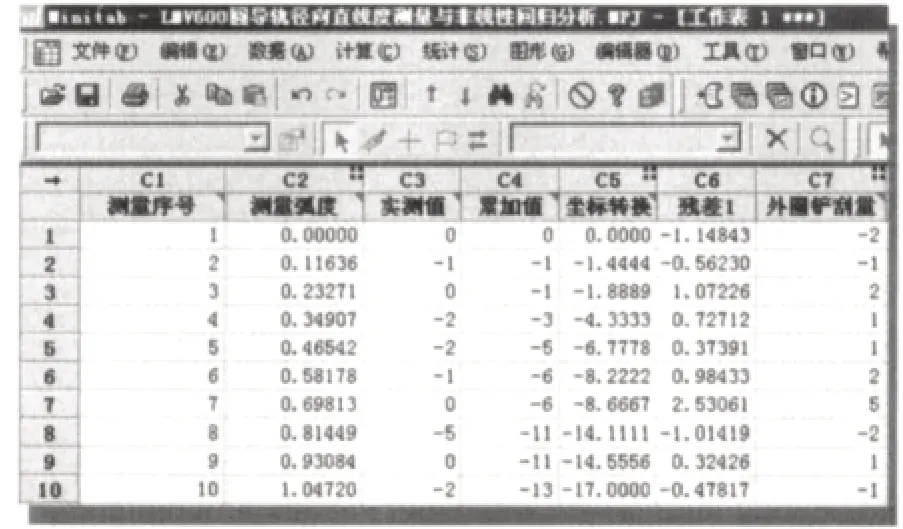
圖9

（2）在第二列C2中輸入測量弧度， 公式為（測量序號－1）×360/54×PI（）/180。

（3）在第三列C3中輸入實測值。

（4）在第四列C4中輸入累加值（累加值在Minitab中不好處理，可以在Excel中處理后復制）。

（5）在第五列C5中輸入坐標轉換后的值，公式為累加值－SUM（實測值）/54×（測量序號－1） 。

（6）然后點擊菜單欄→統計→非線性回歸，輸入公式“X1×S I N（C2+X2×P I（）/180）+X3”，如圖10所示。

上述公式中：X1、X2、X3為回歸變量，其中X1代表sin曲線的振幅，X2為sin曲線起始相位角，X3為sin曲線Y方向變化的常量。

（7）計算后自動求得殘差1。

圖10

（8）為計算實際的鏟刮量，在C7列中輸入如下的公式：殘差1×200×0.01（其中200mm為水平儀測量橋板的長度，0.01mm為水平儀的精度）這樣我們就可以得到非線性回歸后的鏟刮數值，如圖11所示。

（9）如圖12所示：我們可以看到非線性回歸的擬合線圖與計算后的回歸方程，其結論也是精確的。

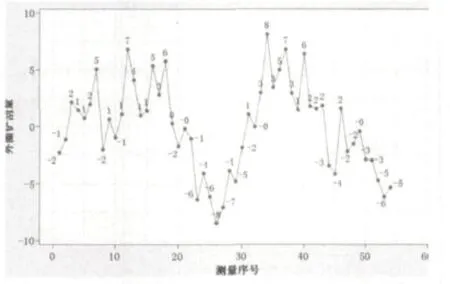
圖11

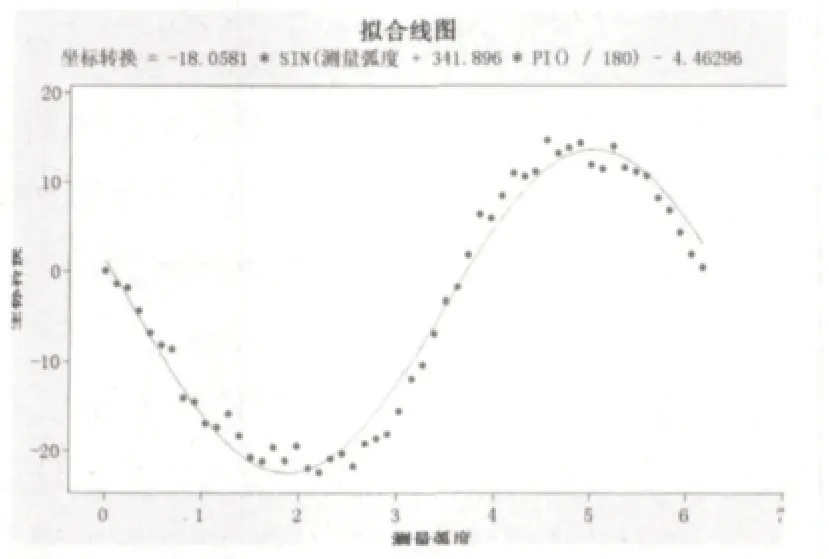
圖12

五、結語

在大型平面圓導軌的測量與鏟刮過程中，主要用切向測量法來測量，測量的數據用非線性回歸的方法處理，與測量起點無關。實際操作過程中將每點計算值標在導軌相應的位置上，按點鏟刮，可以大幅提高效率，以前手工鏟刮需要20天的工作量，現在10天之內就能完成，精度也非常滿意，極大地提高了生產效率。