考慮轉矩波動的電動汽車懸架NVH性能參數優化*

李程祎，左曙光，段向雷

(同濟大學新能源汽車工程中心，上海 201804)

前言

作為電動汽車的一種重要形式，輪邊驅動電動汽車依靠獨立電機驅動單個車輪，并將驅動電機布置在車架或懸架上(而不同于輪轂驅動直接集成在輪胎內的形式)，從而使等效非簧載質量大幅減小，較好地解決了非簧載質量過大帶來的平順性問題[1];通過精確的電子控制來實現理想的車輛穩定性控制(如牽引力控制、制動防抱死控制和橫擺穩定性控制等)，從而改善了車輛的行駛性能。

汽車的NVH性能是衡量汽車水平的一個重要指標[2]。但由于受到供電電流諧波分量、磁場的非正弦分布、定轉子偏心、定子開槽和電機控制系統測量誤差等因素的影響，電機輸出轉矩存在一定幅度的波動[3]。而波動的轉矩直接作用在輪胎上，引起輪胎與地面間縱向和垂向作用力的沖擊與波動，從而導致整車縱向和垂向的振動問題。有研究表明[4－5]，驅動電機的 1、2和 6階轉矩波動是車身結構振動和車內噪聲的主要激勵源，且激勵峰值頻率分布在30～280Hz的中高頻范圍內。

對此，許多學者進行了深入的研究。有些學者就轉矩波動的來源入手，從電機控制的角度出發研究如何抑制電機的轉矩波動[6－7];還有些學者嘗試通過在電機輸出端加入扭轉減振器，試圖從傳遞途徑的角度來衰減轉矩波動。本文中從輪胎-懸架系統的角度出發，將懸架作為輪胎和車身之間的隔振元件考慮。首先在Adams中建立懸架-輪胎-路面多體動力學模型;然后通過響應面法對性能參數進行第1次優化和靈敏度分析;最后對靈敏度較高的參數用梯度下降法進行第2次優化。最終的優化結果明顯減小了轉矩波動對車身振動的影響。

1 懸架-輪胎-路面多體動力學模型的建立

要想正確分析轉矩波動對懸架NVH的影響，首先在Adams/View中建立準確的懸架-輪胎-路面多體動力學模型。為了排除前、后懸架間振動的耦合，只建立基于后懸架的多體動力學模型。

1.1 懸架模型

本文的研究對象是某輪邊驅動電動汽車，其后懸架三維模型見圖1。該車后懸架為扭轉梁結構，采用電機加兩級斜齒輪減速器的驅動形式。減速器的殼體同時也是懸架的縱臂，減速器輸出端連接車輪，驅動電機用螺栓固接在減速器殼體上并驅動減速器輸入端。中間一根扭轉梁分別連接左右懸架的縱臂。

根據三維模型關鍵硬點和拓撲結構，在Adams/View中建立后扭轉梁懸架模型，并做了如下簡化:

(1)所有零部件均為剛體，各部件的慣量參數和質心位置從三維模型中測取;

(2)縱臂與車身間、減振器上端與車身間通過襯套連接;減振器用Spring元件簡化;中間的扭轉梁用Torsion Spring元件簡化;且各彈性元件參數均做線性化處理;

(3)車身以剛體代替，并且車身與大地之間通過平行副連接，即只限制車身俯仰和橫擺自由度，其余自由度不做限制。

1.2 輪胎路面模型

由于須進行的是平順性仿真，且要分析的頻率較高，因此輪胎模型選擇Ftire。它是一種基于柔性環理論、完全非線性的輪胎模型。其適用頻率高達120～150Hz，且仿真精度較高，是MSC公司官方推薦的進行平順性和耐久性仿真的輪胎模型[8]。

在使用Ftire時須注意的是:為了發揮其精度優勢，Adams積分器積分最大步長Hmax設置為0.001s。

為了排除轉矩波動以外的激勵對車身振動的影響，本文中選擇平直路面。

1.3 轉矩波動模型

在縱臂和車輪之間定義單向轉矩，作用方式為Two Bodies，即準確模擬輪胎與減速器之間的作用轉矩和反作用轉矩。

建立考慮轉子磁場前3階諧波影響的永磁同步電機轉矩模型[9]為

式中各符號含義及取值見表1。

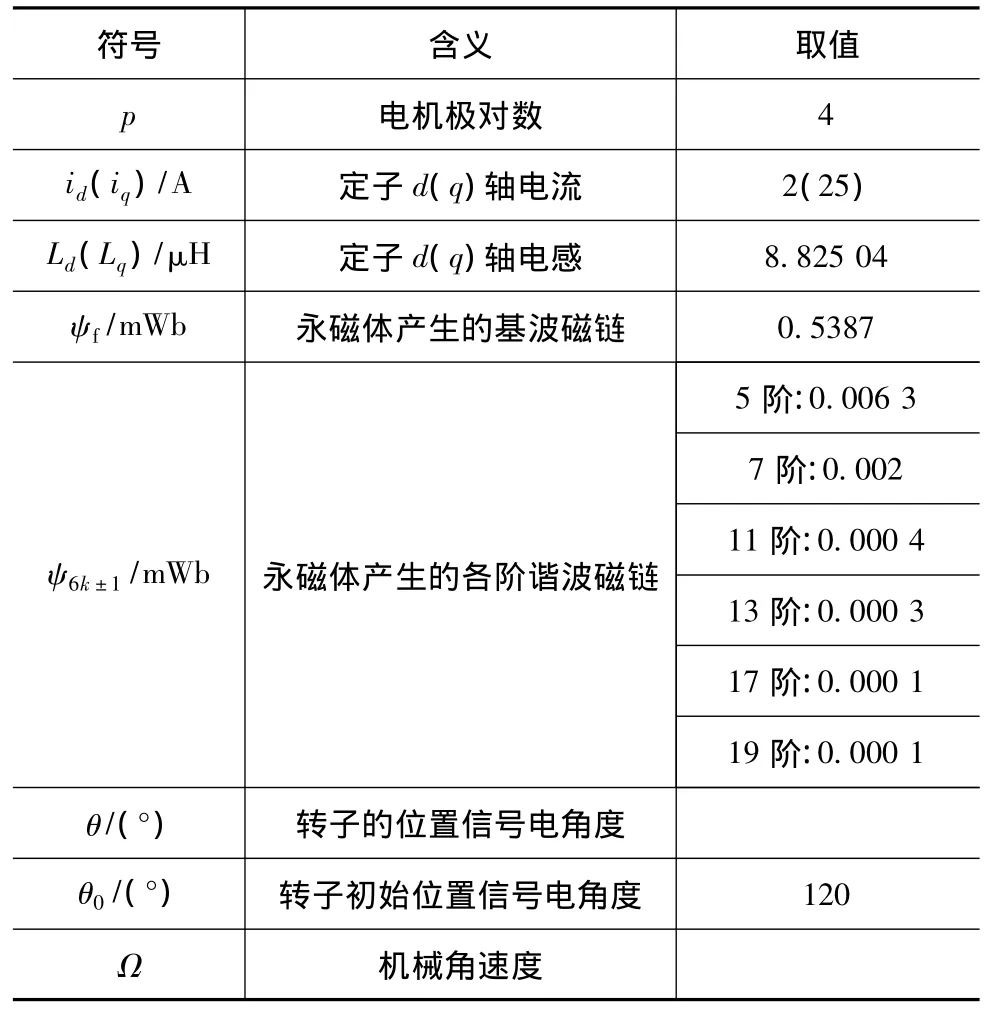
表1 轉矩dq模型符號

轉矩時域曲線如圖2所示。

1.4 完整模型

最終建立的懸架-輪胎-路面多體動力學模型共有5個剛體(左右縱臂、左右減振器上支撐蓋和車身)、30個自由度，如圖3所示。

2 懸架性能參數的兩次優化

懸架的結構參數(如硬點位置)主要影響懸架的運動學特性，而懸架的性能參數(如彈性元件參數)主要影響懸架的彈性運動學特性[10]。本文的目的是優化懸架的NVH性能，故對懸架性能參數進行了兩次優化，具體流程如圖4所示。

2.1 響應面法優化

響應面法是一套數學與統計學相結合的方法，是用一個超曲面來近似替代實際復雜結構的輸入與輸出關系的方法[11]。其基本方法是進行若干次試驗，用最小二乘法回歸模型在優化目標和優化因素之間擬合出一個定量的一次或二次多項式，即響應面。有了響應面，就可不用再進行額外的仿真，只須對表達式用數學的方法求極值，就能算出最優解和對應的因素取值。

進行響應面法分析一般遵循以下5個步驟:(1)定義優化目標;(2)選擇一系列變量作為優化因素;(3)確定各因素的變化水平，根據策略設計試驗表;(4)進行試驗，記錄試驗結果;(5)分析試驗結果，進行優化。

本文中采用的具體步驟如下。

(1)考慮到人體對不同頻率的振動敏感程度不同，參考 ISO2631—1:1997的規定，選擇0～120Hz頻率范圍內車身質心垂向加權加速度均方根值作為優化目標[12]。不同頻率f的頻率加權函數為

(2)所選取作為優化因素的懸架性能參數如表2所示，各因素變化范圍為－50% ～+50%。

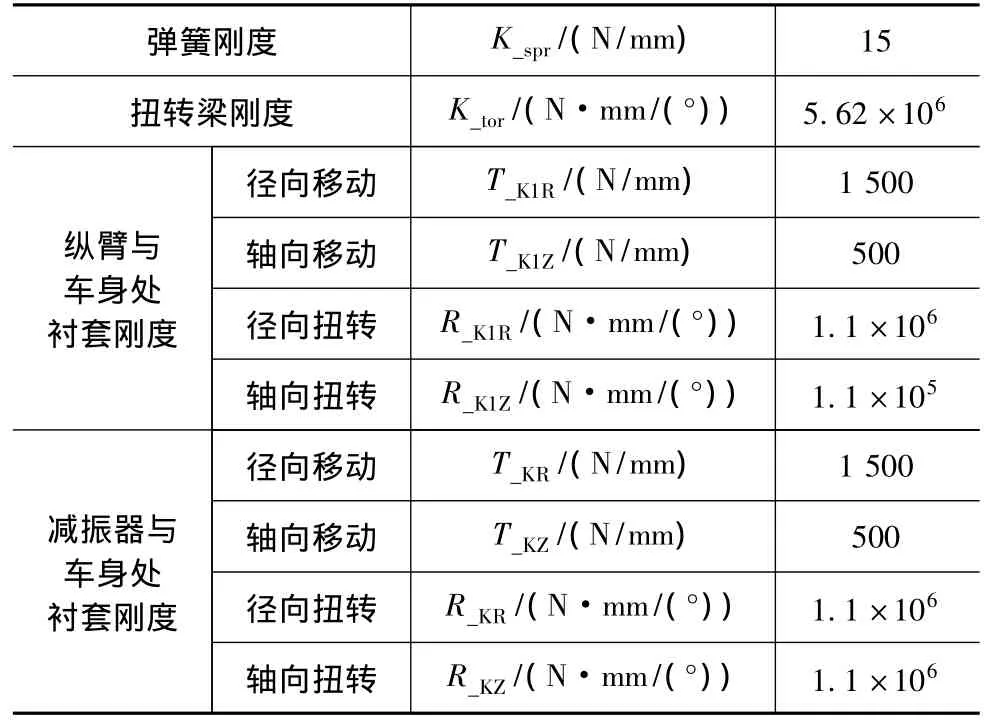
表2 彈性元件參數

(3)常用的試驗設計方法有全因素法、部分因素法、中心復合設計(CCF)、D-最優設計和Box-Behnken。D-最優設計的根本思想是使XTX的行列式最大，其中X是試驗因數輸入矩陣[13]，其最少試驗次數為(n+1)(n+2)/2，其中n是試驗因素的個數。本文中選擇D-最優設計，共進行100次試驗。

(4)仿真由懸架波動的轉矩驅動，在平直路面上直線行駛。仿真時間為10s，仿真步長為0.001s。

(5)響應面法優化后的懸架性能參數見表3。對響應面擬合結果進行模型適應性檢查，得到復相關系數R2=0.962(大于0.95，滿足要求)、修正的復相關系數R2

adj=0.923(大于0.9，滿足要求)，表明擬合精度較高，結果可靠，可做進一步分析。

2.2 靈敏度分析

各性能參數靈敏度如圖5所示。圖中縱坐標指的是某因素取值發生變化后(其余因素仍取初始值)所引起目標值的改變量與目標原始值的比值。正負號表示因素對目標的影響是增大還是減小。因此，縱坐標絕對值越大，表明該因素對目標的影響越明顯。由圖可見，T_K1R和R_K1Z靈敏度相對較大。

2.3 梯度下降法優化

由于響應面法最高只是2次擬合，因此即使擬合精度足夠高，用響應面法算出來的極值仍可能與目標的全局最優解存在一定的偏差。因此，有必要以這一優化為初始點再次進行優化，以便能更準確地找到全局最優解。優化因素就選擇T_K1R和R_K1Z這兩個靈敏度高的參數。

此處利用Adams自帶的優化計算功能:優化方法選擇梯度下降法;優化目標不變，其結果見表3。

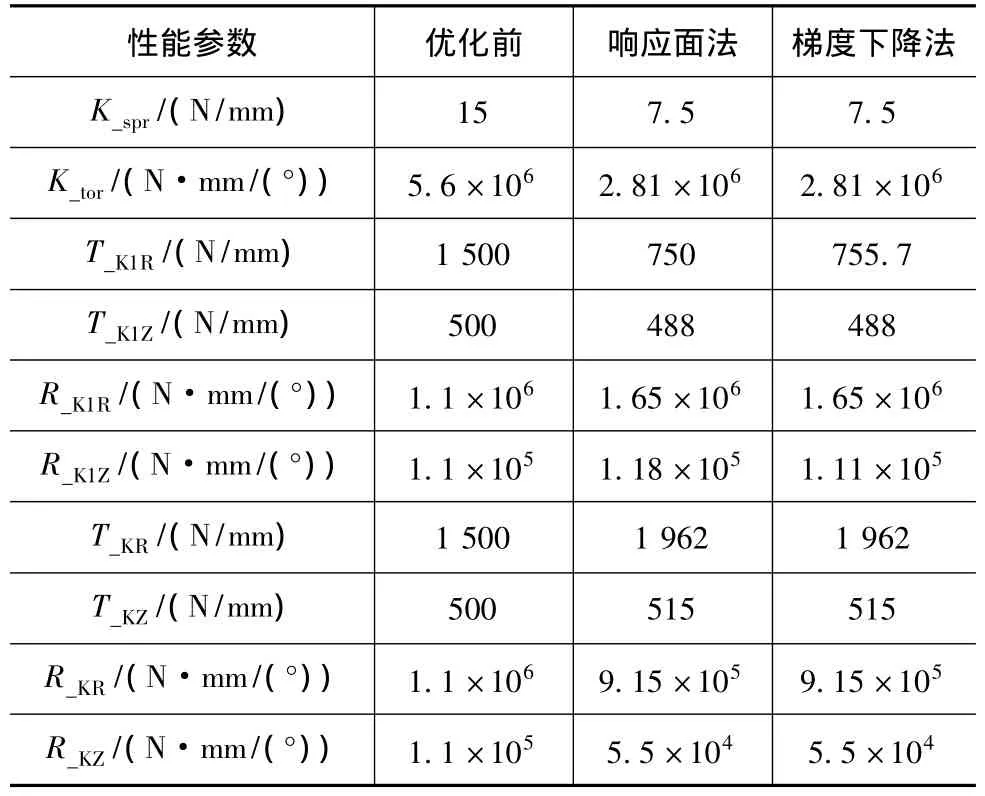
表3 性能參數優化結果

3 結果分析與對比

圖6為優化前后質心垂向加速度的自功率譜。由圖可見，優化后的功率譜在25～100Hz范圍內的幅值明顯降低，能量分布更均勻。

優化前、后的質心垂向加權加速度均方根值對比見表4。可見，經過兩次優化后，下降了11.2%，車身振動明顯減小。

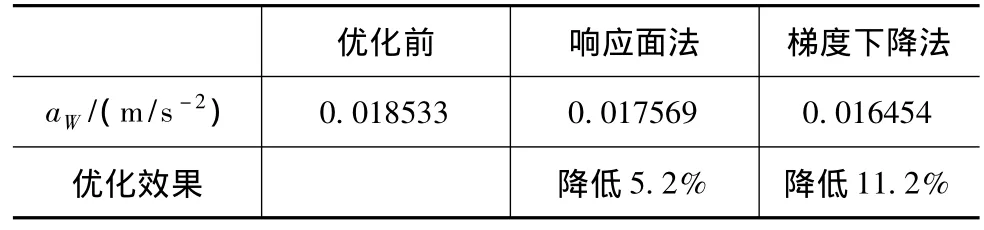
表4 垂向加權均方根對比

此外，通過響應面法和梯度下降法的優化效果對比可以發現，響應面法優化后的結果并不是全局最優的，其依然存在繼續降低的可能性。從而說明本文中進行兩次優化的思路是可行且必要的。

3 結論

(1)通過對懸架性能參數的優化，使車身振動能量降低，且在0～120Hz的頻帶內分布更均勻，明顯改善了由于轉矩波動引起的車身振動，提高了懸架的NVH性能。

(2)通過兩次優化結果的分析與比較，可以看出單純用響應面法得到的結果仍不是全局最優解，有必要通過后續的二次優化來求得全局最優解。

[1]陳辛波，鐘再敏，唐峰，等．減小單縱臂懸架輪邊電驅動系統等效簧下質量結構及方法:中國，102092256 A[P]．2011－06－15．

[2]李欣冉，陳曉新，王家恩，等．橡膠襯套對汽車懸架系統NVH性能影響研究[J]．合肥工業大學學報(自然科學版)，2012(5):581－584．

[3]張立軍，錢敏，余卓平．輪轂電機-輪胎總成非線性動力學特性仿真分析[C]．第五屆中國智能交通年會暨第六屆國際節能與新能源汽車創新發展論壇優秀論文集(下冊)．北京:電子工業出版社，2009．

[4]王建，張立軍，余卓平，等．燃料電池轎車電機總成的振動階次特征分析[J]．汽車工程，2009，31(3):219 －223．

[5]于增亮．輪轂電機驅動電動車懸架系統振動特性[D]．上海:同濟大學，2010．

[6]陳冬雪，宗長富，何磊，等．輪轂電機的轉矩脈動抑制方法研究[J]．科學技術與工程，2012(8):1811 －1815．

[7]劉和平，趙智輝，尹賢亮．新型輪轂電機轉矩脈動抑制方法應用[J]．微電機，2011(3):21 －24．

[8]陳軍．MSC．ADAMS技術與工程分析實例[M]．北京:中國水利水電出版社，2008．

[9]李景燦，廖勇．考慮飽和及轉子磁場諧波的永磁同步電機模型[J]．中國電機工程學報，2011(3):60 －66．

[10]劉慧斌．Strut-Links型后懸架硬點及襯套剛度優化方法的研究[D]．長春:吉林大學，2011．

[11]王延克．基于響應面法的汽車懸架系統優化設計[D]．成都:西南交通大學，2009．

[12]陳曉新．基于剛柔耦合的整車動力學建模與懸架隔振性能分析[D]．合肥:合肥工業大學，2010．

[13]隋允康，宇慧平．響應面方法的改進及其對工程優化的應用[M]．北京:科學出版社，2011．