基于證據理論的航天產品的非參數可靠性評估方法*
周 曠 師義民 馬麗娜
西北工業大學,西安 710072
航天產品多為復雜新型產品,由于時間、經費、保密等因素的限制,產品壽命的分布類往往未知。隨著可靠性水平的不斷提高,其貯存壽命和使用壽命通常都比較長。要獲得此類產品的壽命數據,按照傳統的壽命試驗方法就是通過自然環境貯存、長期監測和數據統計來得到。雖然這種試驗技術獲得的數據比較真實,得到的結論也比較可信,但是試驗周期一般較長,不能跟上產品的更新改良速度。同時,對影響新型產品失效的因素也沒有理論上的完整認識。非參數統計方法由于不受限于分布類型,在這種情況下就發揮著重要的作用。對樣本先驗信息的缺乏在信息學上稱之為不確定性,是壽命數據統計分析中常遇到的問題[1]。因此,許多學者研究了不確定推理方法在可靠性評估中的應用,其中常用的方法有:不精確概率論(又稱為區間概率論)[2]、模糊集理論[3]、隨機集理論[4]等。
Dempster-Shafer證據理論可以有效地處理不確定信息,而且提供了融合多源證據的組合規則,近來已被廣泛應用在信息融合[5],圖像處理[6]等領域,已有許多學者將其應用在可靠性評估當中。文獻[7-8]研究了DST融合可靠性中不確定信息的方法。這些文章利用的都是相似產品的可靠性信息或者專家的經驗信息。不同的是,本文用假設和證據理論提出了一種只使用具有缺失信息(分布類未知)的樣本數據壽命分析方法。首先利用假設基于樣本數據構建了分布函數的概率上下限,然后將其轉化為證據理論框架下的基本信度分配(BBA),最后在可轉移信度模型(TBM)下將其轉換為一種概率度量,可據此對產品的壽命特征進行評估。數值實例表明了本文提出方法的可行性和有效性。
1 相關理論基礎
1.1 DST和TBM
設Θ={θ1,θ2,…,θN}表示X所有可能取值的論域集合,且所有在Θ內元素是互不相容的,稱Θ為X的識別框。證據理論是建立在冪集2Θ={A∶AΘ}上的[9]。
定義1 設Θ是X的識別框架,則函數m∶2Θ→[0,1]稱為2Θ上的基本信度分配(BBA)函數,如果滿足:
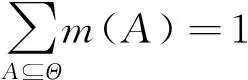
(1)
其中,m(A)表示了對A的直接支持,通常稱為A的mass值。對空集Φ分配的基本信度m(Φ)代表了識別框架的不一致性和不完整性。滿足m(A)>0的子集A稱為焦元,所有焦元的集合F={A|m(A)>0}稱為Θ的核。稱二元組(F,m)為定義在Θ上的一條證據。按照式(2)和(3)定義信任度函數(bel)和似然度函數(pl)。
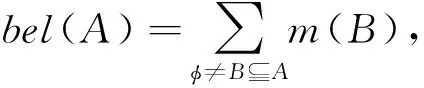
?AΘ
(2)
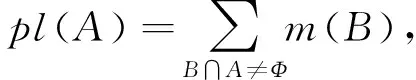
(3)
bel(A)和pl(A)分別代表了對命題A的最低支持和最高支持。
可轉移信度模型[10]是一種定量描述信度的數學模型。這是一個兩層模型:1) 建立和度量經驗信度的信度層(creedal level);2) 用于決策的概率層(pignistic level)。
在TBM中,可用Pignistic概率轉換公式將BBA轉換成一種概率度量。最常用的轉換方法是平均分配法(Smets法),認為每一個元素出現的概率相等,因此把多元素命題的BBA值平均分配給所包含的元素[11]。
(4)
其中|A|為集合A的勢。
1.2 A(n)假設
Hill提出的A(n)假設為樣本分布完全未知時的統計預測問題提供了依據[12-13]。
定義2 設xi,i=1,2,…,n是從一有限總體中抽取的一組樣本,x(i)為相應的次序統計量。定義A(n):
1)觀測變量X1,X2,…,Xn是可交換的;
2)以概率0無重復觀測樣本值(稱之為結);
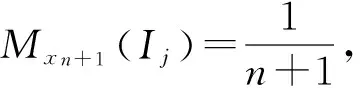
下面對A(n)從可交換性的角度進行直觀解釋。由于只有樣本數據{x1,x2,…,xn},所以對后驗數據只有一個位置的認識,而沒有先后的概念。這也反應了先驗信息的缺乏。許多學者對這一假設從理論上給予了證明。Hill給出了對A(n)的一個非參數Bayesian證明方法[14],Lane和Sudderth用博弈論的方法對A(n)進行了討論[15]。利用A(n)假設并不能得到變量的精確概率分布,但是De Finetti提出了根據A(n)來構建概率上下限的方法[16],這和Walley的不精確概率理論的思想是一致的。關于這方面的詳細討論和應用可參閱文獻[17~18]。
Coolen把A(n)拓展到截尾數據模型[19],稱為rc-A(n)。設在壽命試驗中有n(n=u+v)個事件發生時刻x1,x2,…,xn,其中包括u個失效時刻
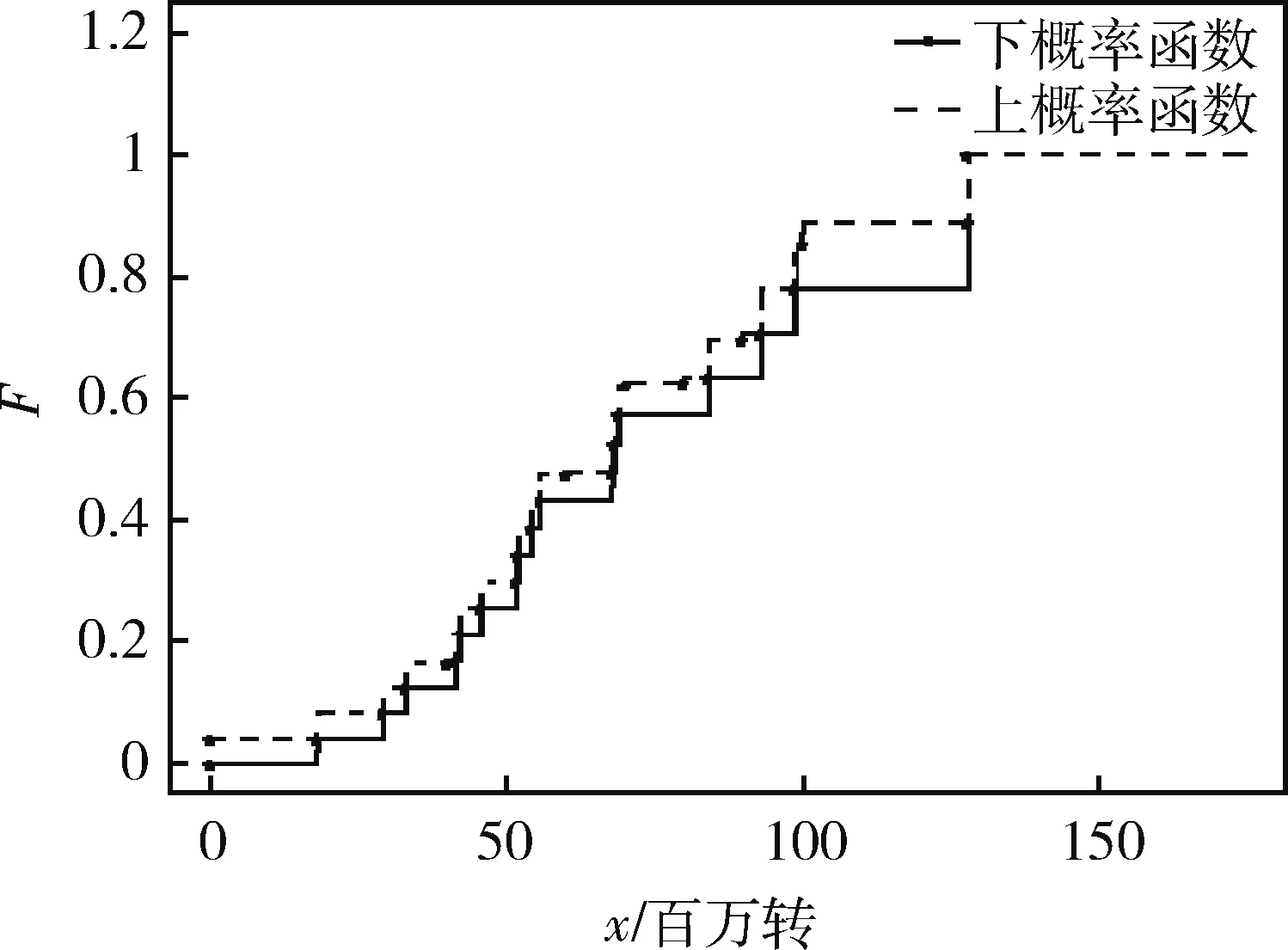
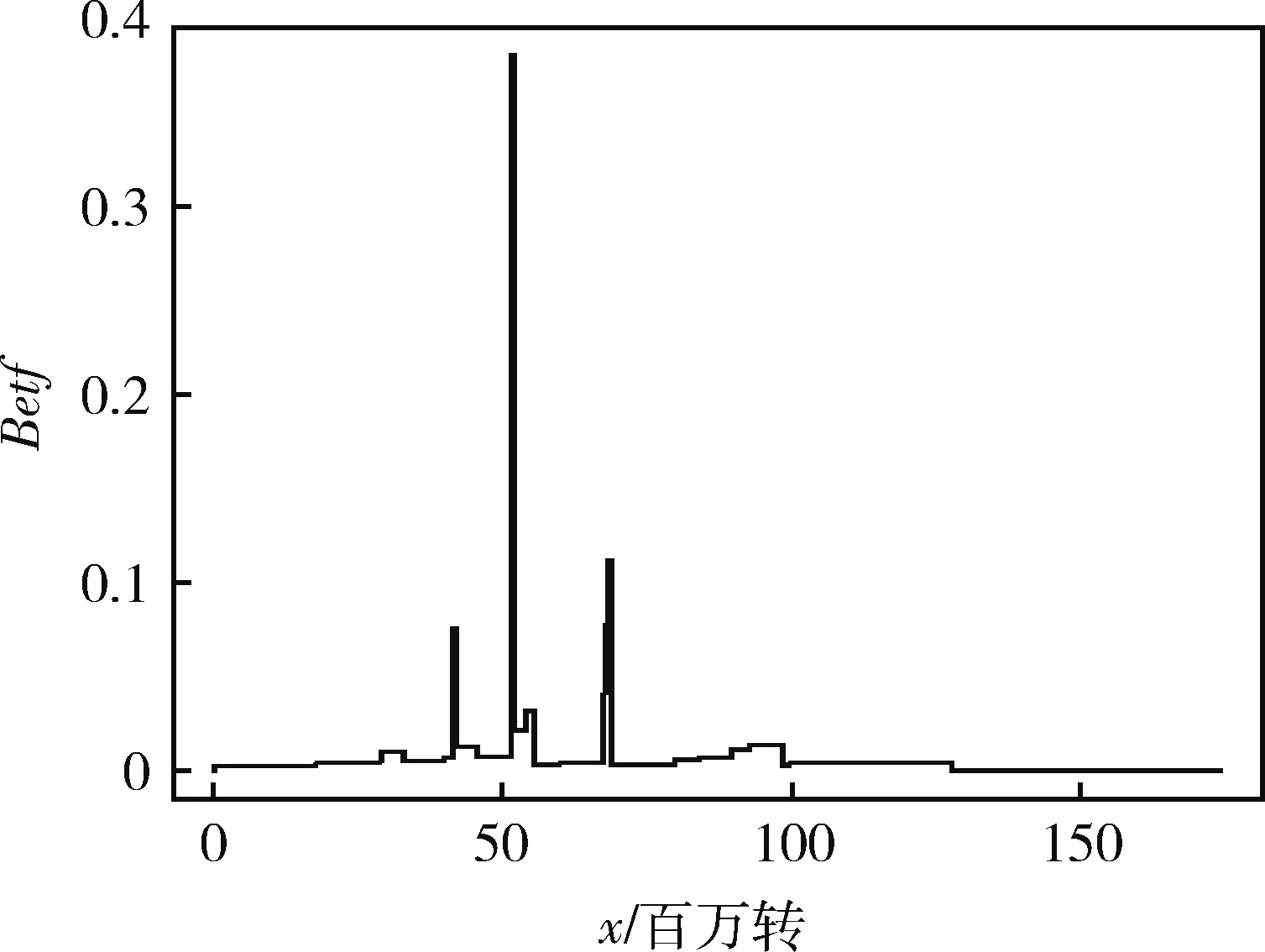
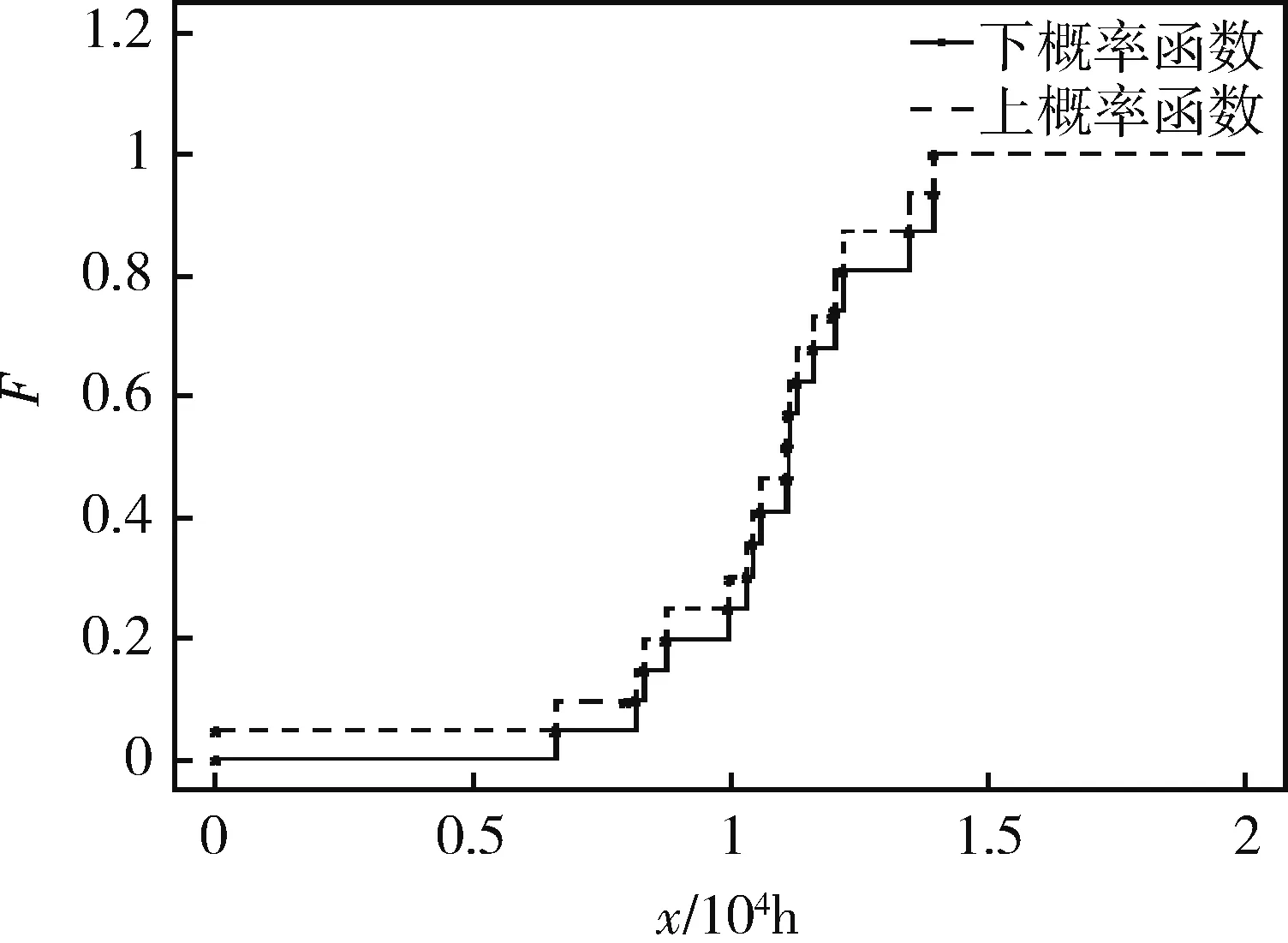
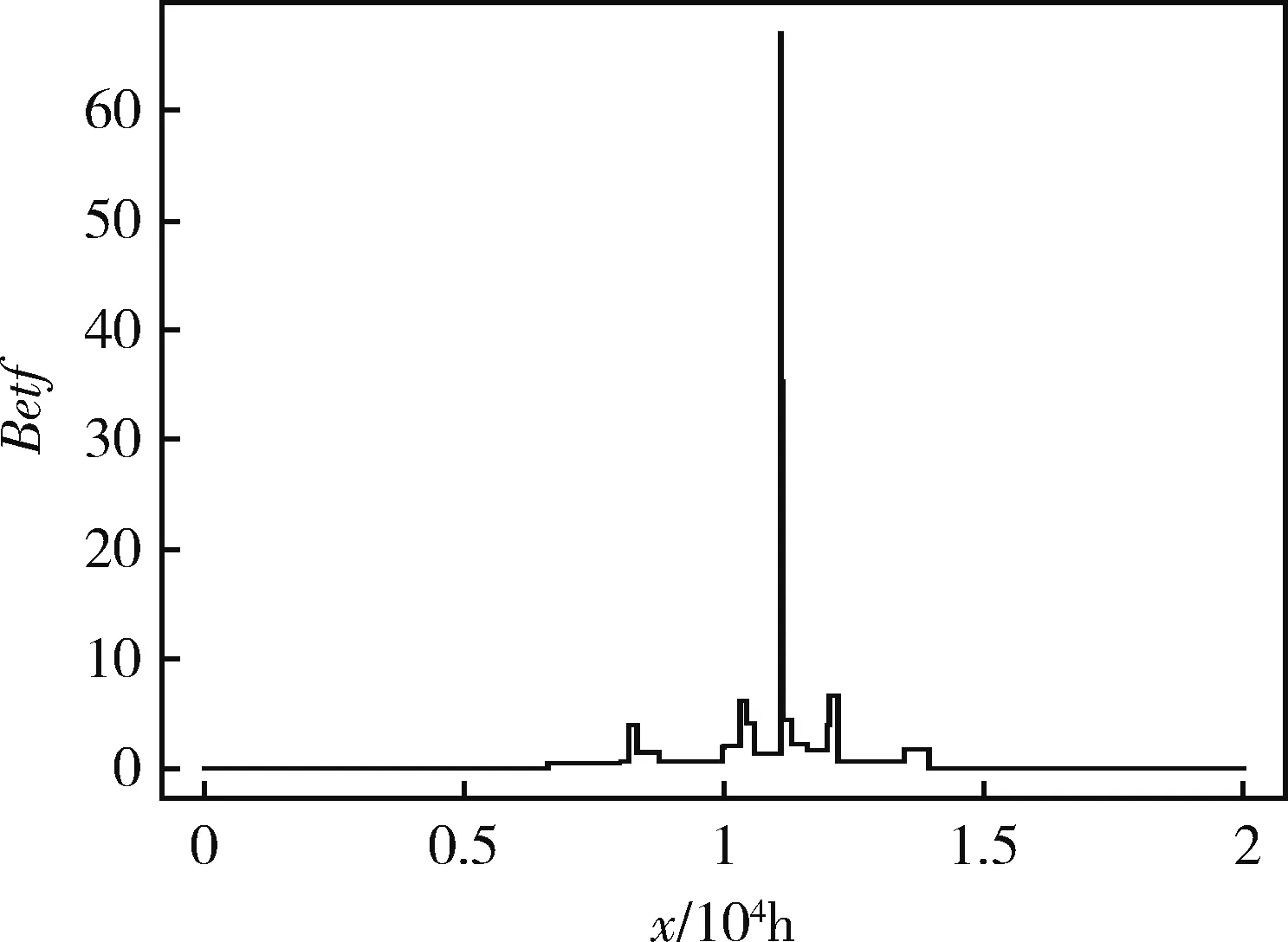
0 (5) 和v個截尾時刻 0 (6) 則rc-A(n)定義如下: (7) 其中i=0,1,…,u,k=1,…,li,t(0)=0,t(u+1)=∞。 如果上式中的連乘發生在空集上,則令其值為1。 這一關于截尾樣本數據的后驗假設既包含了對樣本分布等先驗信息的無知,也包含了截尾形式的完全隨機性。如果樣本中沒有截尾數據(完全樣本), 則rc-A(n)退化為A(n)。 Augustin和Coolen給出了基于A(n)假設的構建事件Xn+1∈B上下概率限的方法[17]。類似地,這里給出根據rc-A(n)假設的構建方法。 (8) (9) 公式(8)和(9)定義的概率上下限是最小的上界和最大的下界[19]。 考慮事件Xn+1∈(t,∞),為了和下文構建mass函數時一致,定義關于可靠度函數(R(t))的上概率函數和下概率函數: (10) (11) 其中 P(Xn+1∈(t(i),t(i+1))=MXn+1(t(i),t(i+1))+ 不可靠度函數(分布函數) F(t)=1-R(t) 的概率上下限分別為: (12) 和 (13) 易知,關于分布函數的上概率函數左連續,下概率函數右連續,而且都是階梯函數。在不引起混淆的情況下,在后續討論中,記 算法1: (1)初始化變量,令k,i,j=1,P0=0; mk=F(x*i)-pk-1,pk=F(x*i) 令k=k+1,i=i+1,返回步驟(2)。 令k=k+1,j=j+1,返回步驟(2)。 由上節算法得到的BBA的焦元區間是[0,1]子區間,該證據的識別框架為[0,1]的子區間的集合 Θ={[a,b]|0≤a 按照Smets平均分配思想,如果已知θ上的BBA,可得到區間A的Pignistic概率為 ?A?Θ (14) 這個公式有一個簡單的數學解釋:區間B上的mass值,將平均分配給所有與它有交集的區間。對于單點概率,可類似地有, ?θ∈Θ (15) BetfXn+1為關于下一個觀測變量的Pignistic概率密度。根據TBM模型,對于Xn+1的“決策”可根據此進行。例如,可以用該概率分布的期望預測下一個變量Xn+1的平均壽命,用BetPXn+1(t,∞)表示t時刻的可靠度。 下面用2個數據集對本文提出的方法進行驗證。例1是一個真實數據集,例2是一個用人工方法產生的模擬數據集。 例1 Lawless給出了一種球狀軸承的壽命數據集。數據是23個軸承在失效前的轉數(百萬次): 17.88, 28.92, 33.00, 41.52, 42.12, 45.60, 48.80, 51.84, 51.96, 54.12, 55.56, 67.80, 68.64, 68.64, 68.88, 84.12, 93.12, 98.64, 105.12, 105.84, 127.92, 128.04, 173.40. 選取6個截尾(移走)時刻:40.00, 60.00, 70.00, 80.00, 90.00, 100.00,試驗中觀測到的數據(百萬轉數)如表1所示。 表1 軸承壽命數據(>表示截尾數據) 由公式(8)和(9)得到X24的分布函數的上下限,如圖1所示。 圖2分別描述了此壽命變量的Pignistic概率。X24的平均壽命為56.6384(百萬轉)。 例2 設某型液體火箭發動機服從雙參數威布爾分布WeiBull(2,5)。 隨機產生容量為20個服從威布爾分布WeiBull(2,5)的樣本。隨機選取3個截尾時刻0.80,1.00,1.20(單位:104h)。生成的隨機樣本如表2所示(單位:104h)。圖3和4分別描述了分布函數的上下概率限和Pignistic概率圖。X21的平均壽命為1.3488, 這和理論值1.0547比較接近。 例2雖然給出了元件的壽命分布,但是只應用上節提出的算法進行計算并未使用。從例1和例2可以看出,本文提出的方法使壽命分布未知的產品可靠性評估帶來了極大的方便,而且保證了評估結果的合理性。 圖1 X24分布函數的上下概率 圖2 X24 Pignistic概率 圖3 X21 分布函數的上下概率 0.66051.03071.1621>0.80001.0424>1.20000.81701.05601.20600.83411.11091.21920.87711.11201.34970.99701.11401.3973>1.00001.1304 圖4 X21 Pignistic概率 本文提出了一種基于證據理論的非參數預測方法,并將其應用于新型航天產品的可靠性評估。首先利用樣本數據構建了分布函數的概率上下限,然后將其轉化為證據框架下的基本信度分配,最后利用可轉移信度模型的Pingstic概率轉換方法得到了關于未來觀測變量的概率度量,可據此對產品的壽命特征進行評估。數值實例表明本文得出方法的正確性和有效性。由于該方法僅利用了樣本數據, 這對樣本分布類無知的情況下評估問題具有重要意義。要把本文提出的方法適用于一般的截尾模型,如定數截尾試驗、逐步截尾試驗等,這就要放寬A(n)假設中樣本數據無重復值的限制,這將是下一步研究的方向。 參 考 文 獻 [1] Aven T,Zio E.Some Considerations on the Treatment of Uncertainties in Risk Assessment for Practical Decision Making[J].Reliability Engineering and System Safety, 2011, 96(1): 64-74. [2] Joslyn C,Kreinovich V.Convergence Properties of An Interval Probabilistic Approach to System Reliability Estimation[J].International Journal of General Systems ,2005, 34(4): 465-482. [3] Hafaifa A,Laaouad F,Guemana M.A New Engineering Method for Fuzzy Reliability Analysis of Surge Control in Centrifugal Compressor[J].American Journal of Engineerinig and Applied Sciences, 2009, 2(4):676-682. [4] Guo H,Xia Z,Chen L,et al.Estimation of Reliability with Hybrid Uncertainties in the Unified Framework of Random Set Theory[C].Intelligent Computation Technology and Automation,2009.ICICTA′09.Second International Conference on IEEE,2009,2:507-512. [5] 吳瑕,周焰.模糊傳感器與區間型多屬性決策的信息融合方法[J].宇航學報, 2011,32(6):1409-1415.(Wu X, Zhou Y.Methods of Information Fusion Based on Fuzzy Sensor and Interval Multi-Attribute Decision-Making [J].Journal of Astronautics, 2011, 32(6):1409-1415.) [6] 孫子文,李慧,紀志成.基于D-S證據理論的融合圖像隱寫分析[J].控制與決策, 2011, 26(8):1192-1196.(Sun Z, Li H, Ji Z.Fusion Image Steganalysis Based on Dempster-Shafer Evidence Theory [J].Control and Decision, 2011, 26(8):1192-1196.) [7] Wan J,Jiang T,Li X,et al.An Information Fusion Method for Reliability Based on D-S Evidential Theory [C].Industrial Engineering and Engineering Management(IE&EM),2010 IEEE 17th International Conference on IEEE,2010:920-923. [8] Smets P.The Transferable Belief Model for Expert Judgments and Reliability Problems[J].Reliability Engineering & System Safety,1992,38(1):59-66. [9] Shafer G A.Mathematical Theory of Evidence [M].Princeton, New Jersey: Princeton University Press, 1976. [10] Smets P,Kennes R.The Transferable Belief Model [J].Artificial Intelligence, 1994, 66(2): 191-243. [11] Smets P.Decision Making in the TBM: the Necessity of the Pignistic Transformation[J].International Journal of Approximate Reasoning, 2005, 38(2):133-147. [12] Hill B.M.Posterior Distribution of Percentiles: Bayes’ Theorem for Sampling from a Population[J].Journal of the American Statistical Association,1968, 63:677-691. [13] Hill B M.De Finetti’s Theorem, Induction, and A(n)or Bayesian Nonparametric Predictive Inference (with discussion)[J].Bayesian Statistics,1988,3: 211-241. [14] Hill B M.Parametric Models for A(n): Splitting Processes and Mixtures [J].Journal of the Royal Statistical Society.Series B(Methodological),1993,55,:423-433. [15] Lane D A, Sudderth W D.Diffuse Models for Sampling and Predictive Inference[J].The Annals of Statistics.1978,6,:1318-1336. [16] De Finetti B.Theory of Probability (2 volumes)[M].Wiley, London, 1974. [17] Augustin T, Coolen F P A.Nonparametric Predictive Inference and Interval Probability[J].Journal of statistical planing and inference, 2004,124(2):251-272. [18] Coolen F P A,Coolen-Schrijner P,Yan K J.Nonparametric Predictive Inference in Reliability [J].Reliability Engineering and System Safety,2002,78(2):185-193. [19] Coolen F P A, Yan K J. Nonparametric Predictive Inference with Right-censored Data [J].Journal of statistical planing and inference,2004,126(1):25-54. [20] Kriegler E, Held H. Utilizing Belief Functions for the Estimation of Future Climate Change [J].International Journal of Approximate Reasoning,2005, 39(2):185-209. [21] Lawless J F.Statistical Models and Methods for Lifetime Data [M].Wiley, New York,1986.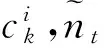
2 壽命估計模型
2.1 基于rc-A(n)的不精確概率
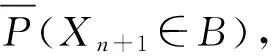
2.2 mass函數的構建
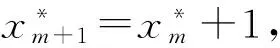
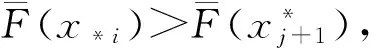
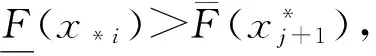
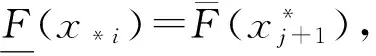
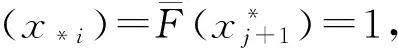
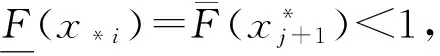
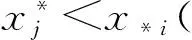
2.3 Pignistic 概率決策
3 數值實例


4 結論

