基于有限元法和ABAQUS仿真的蛛網結構分析

傅瞳 曹蕾娜

摘 要 常見的蛛網結構即由一個中心伸出的若干放射狀絲線和圍繞這個中心的螺旋狀絲線構成的網狀結構。然而，究竟是哪一種絲線結構能使得蛛絲達到它的最佳利用狀態呢？文章探討了基于有限元法和ABAQUS仿真的蛛網結構。

關鍵詞 蛛網結構 有限元 ABAQUS仿真

中圖分類號：TG95 文獻標識碼：A

1 概述

世界上生存著許多種類的蜘蛛，而其中的大部分種類都會通過結網來進行捕食。相關研究論文指出，蛛絲本身的性質及蛛網的結構使得整張網經久耐用，蛛絲比頭發絲還細，但強度卻超過同等粗細的鋼鐵，它的特性早就引起科研人員的關注。與蛛絲這種特性相結合的是其常見的蛛網結構，即由一個中心伸出的若干放射狀絲線和圍繞這個中心的螺旋狀絲線構成的網狀結構，保證了蛛網經久耐用。有研究顯示，在均勻受力的情況下，整張蛛網能抵抗颶風強度的氣流。那么我們自然會對這種結構好奇，我們自然會提出疑問：究竟蜘蛛網織成怎樣的結構才是最合適的？

2 問題的分析

通過查閱資料和分析現實生活中蜘蛛網的形狀和結構，結合結構力學的相關知識，蜘蛛要達到捕食目的，并保持網的完整性，不被破壞，蜘蛛網的結構和飛蟲撞擊的角度起到一定的作用，由于飛蟲撞擊的角度隨機性較大，又因為我們在此時對各種網進行比較，得出何種蜘蛛網最為合適，所以在此飛蟲的撞擊角度不予考慮。

我們認為昆蟲和蛛網的關系，在無自然因素影響下是可以模糊化模型為密度稀疏的彈性膜面與在其上施加適當壓力。如前假設，蜘蛛網是對稱結構，因為這樣的平面結構在受到力的作用時會比不對稱的穩定。在進行仿真時，我們考慮到了蜘蛛的吐絲量也是關系蛛網結構穩定的一個因素，所以，我們設定模型的面積一定。

接著，我們根據所查資料和相關數學知識，確定了候選仿真模型：三角形蜘蛛網、正多邊形蜘蛛網（以正六邊形為例）、螺線型蜘蛛網。對這些結構進行分析，觀察其對沖擊載荷的承載能力，并與其他結構進行比較，得出最合適的蜘蛛網結構。

3 模型的建立

3.1 方法選取

3.1.1 有限單元法

有限單元法，是一種有效解決數學問題的解題方法。其基礎是變分原理和加權余量法，其基本求解思想是把計算域劃分為有限個互不重疊的單元，在每個單元內，選擇一些合適的結點作為求解函數的插值點，將微分方程中的變量改寫成由各變量或其導數的結點值與所選用的插值函數組成的線性表達式，借助于變分原理或加權余量法，將微分方程離散求解。采用不同的權函數和插值函數形式，便構成不同的有限元方法。

在有限元方法中，把計算域離散剖分為有限個互不重疊且相互連接的單元，在每個單元內選擇基函數，用單元基函數的線形組合來逼近單元中的真解，整個計算域上總體的基函數可以看為由每個單元基函數組成的，則整個計算域內的解可以看作是由所有單元上的近似解構成。在河道數值模擬中，常見的有限元計算方法是由變分法和加權余量法發展而來的里茲法和伽遼金法、最小二乘法等。

有限元插值函數分為兩大類，一類只要求插值多項式本身在插值點取已知值，稱為拉格朗日（Lagrange）多項式插值；另一種不僅要求插值多項式本身，還要求它的導數值在插值點取已知值，稱為哈密特（Hermite）多項式插值。單元坐標有笛卡爾直角坐標系和無因次自然坐標，有對稱和不對稱等。常采用的無因次坐標是一種局部坐標系，它的定義取決于單元的幾何形狀，一維看作長度比，二維看作面積比，三維看作體積比。在二維有限元中，三角形單元應用的最早，近來四邊形等參元的應用也越來越廣。對于二維三角形和四邊形電源單元，常采用的插值函數為有Lagrange插值直角坐標系中的線性插值函數及二階或更高階插值函數、面積坐標系中的線性插值函數、二階或更高階插值函數等。

3.1.2 有限單元法求解流程

有限元運用在實際問題求解過程中，主要有七個主要步驟，分別是：①對結構進行離散；②形成單元的剛度矩陣和等效結點載荷列陣；③集成結構的剛度矩陣和等效結點載荷列陣；④引入強制邊界條件；⑤求解有限元求解方程，得到結點位移；⑥計算單元應變和應力；⑦進行必要的后處理。

4 問題的求解

4.1 蜘蛛網模型

我們認為昆蟲和蛛網的關系，在無自然因素影響下是可以模糊化模型為密度稀疏的彈性膜面與在其上施加適當壓力。如前假設，蜘蛛網是對稱結構，所以，我們這里并沒有整網分析，而是取其同一方位的三分之一網進行了受力仿真。

我們使用ABAQUS軟件平臺，建立了如下三種蛛網模型并進行了求解：三角形蜘蛛網、正多邊形蜘蛛網（以正六邊形為例）、螺線型蜘蛛網。

4.2 計算結果

4.2.1三角形蜘蛛網模型

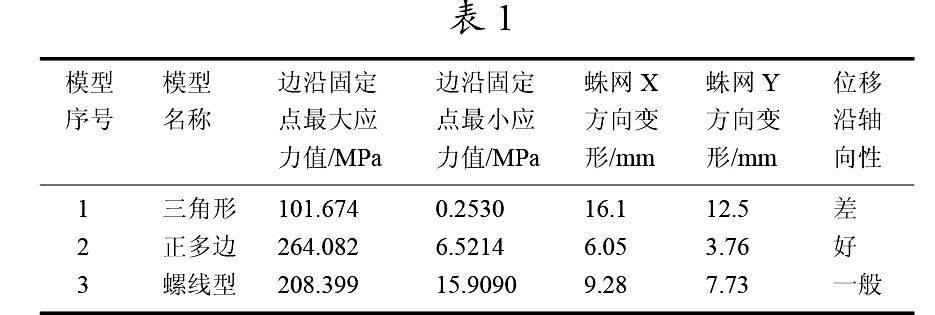
綜合數據可知，三角形模型的蛛網邊沿固定點的值為101.674、84.9822、0.25、0.30、可見其受力是很均衡的，內部的大壓力沒有迫使外部牽拉結構的帶來負擔，但其位移的不沿軸向分布卻說明了其結構的不合理性。

4.2.2正多邊形蜘蛛網（以六邊形為例）

綜上所述，我們可以發現邊沿其固定點的應力值為：264.082、244.286、8.8847、6.5214可見其受力是很均衡的，內部的大壓力沒有迫使外部牽拉結構的帶來負擔，而且其位移的基本是沿軸向分布的，說明其結構是很合理的。

4.2.3螺線型蜘蛛網模型

綜上所述，我們可以發現邊沿其固定點的應力值為：208.399、138.94、15.9089、20.6322可見其受力是很均衡的，內部的大壓力沒有迫使外部牽拉結構的帶來負擔，但從其位移圖中我們可以發現沿軸向分布的位移是有偏移軸向的趨勢的，而且有的已經明顯的錯位，所以，螺線型的模型應該是介于三角形模型與正多邊型模型之間的一類模型。

4.3 結果分析（表1）

正多邊形下的蜘蛛網，對外界壓力的抵消即沿軸向的位移最小，外壓消弱能力最強，結構最穩定。

5 模型的優缺點分析

5.1 模型的優點分析

（1）有限單元法的基礎理論比較成熟，已經成為當今成效最為顯著的數值分析方法。（2）有限單元法適用性強，試用于任何支撐條件和載荷的模型。（3）本文建立的蛛網模型合理，計算精確度較高。（4）模型采用了數值計算與軟件相結合的方法，使問題的解決更加嚴密。（5）基于膜與壓力的力學控制方程適用范圍較廣。（6）離散的控制方程形式規范，便于編制通用的計算機程序。（7）模型建立和求解符合實際，為一些仿生學建筑提供了理論依據。

5.2 模型的缺點分析

（1）由于時間的原因不能對模型進行更深一步的計算。（2）模型計算過程中存在一些誤差，改進相對困難。

參考文獻

[1] 劉少杰.客機水面迫降時的姿態.內蒙古：數學建模挑戰賽，2011.

[2] 槽德欣.計算方法.中國礦業大學出版社，2004.

[3] 張興永.數學建模精彩集訓材料.中國礦業大學出版社，2008.