撐起“猜想”的桅桿，向思維更深處漫溯

周群梅　董江青

摘 要：猜想，是發現的起點，是探索的動力；猜想，是一種思維方式，是一種體驗過程，是一種學習方法。然而，在教學過程中，教師往往過分地強調數學的嚴謹性和科學性，而忽略了對學生猜想能力的培養。數學課堂應該讓學生敢于猜想，善于猜想，學會數學猜想的方法。以《長方形的周長》教學為例，談了在小學數學教學中如何培養學生猜想的能力。

關鍵詞：數學；猜想；思維；能力

猜想是對研究的對象或問題進行觀察、實驗、分析、比較、聯想、類比、歸納等，依據已有的材料和知識做出符合一定的經驗與事實的推測性想象的思維形式。猜想是重要的數學能力之一，是一種難度較大的跳躍式的創造性思維。但在教學過程中，我們往往過分地強調數學的嚴謹性和科學性，而忽略了對學生猜想能力的培養，以致學生在解答題目過程中常常出現謹小慎微、思維不活躍、想象力不豐富、創造力低下的現象。著名科學家牛頓說：“沒有大膽的猜想，就不可能有偉大的發現和發明。”因此，小學數學教學應培養學生猜想的能力，讓學生撐起“猜想”的桅桿，向思維更深處漫溯。筆者在《長方形的周長》教學中作了嘗試。

一、加強感知體驗，預熱猜想

感知是學生認識的開始，沒有正確的感知就不可能認識事物的本質和規律。心理學研究表明：學生感知越豐富，建立的表象越清晰，就越能發現事物的規律，獲得知識。如，在教學《長方形的周長》中，筆者先組織學生以下四步學習。（1）導學。先說一說關于長方形，你已經知道了什么？再拋出問題：黑板長30分米，寬10分米，把它四周圍上花邊，花邊至少長多少分米？然后順勢揭示課題。（2）試學。請學生獨立計算這個長方形的周長，并準備好在小組內進行交流。（3）展學。先請學生根據以下要求進行小組交流。①明確分工：誰先說，誰記錄；②每人先交流一種方法；③把算式記錄在“記錄單”上；④選好小先生，準備上臺匯報。再組織學生進行全班展示交流，并得出三種不同的方法。（4）研學。先請學生仔細觀察這三種方法，然后說說有什么異同。

如此四步教學，教師引導學生動手做、動腦想、動口說、動眼看，使學生在做一做、算一算、想一想、說一說、看一看中獲得豐富的感性認識，建立清晰的表象，搭建起知識結構物化與內化的橋梁，讓學生充分感知體驗的同時，也為后面的合理猜想作了充分必要的準備。

二、挖掘教學材料，啟迪猜想

任何數學猜想都是學生的直覺判斷，可是它必須建立在一定的知識和數學思考上，也就是說它要有一個支撐點和生長點。數學知識、數學方法等方面往往存在著某種內在的聯系，這些都可以作為數學猜想的生長點。因此，我們在新知的教學中要提供有連接性的教學材料，創設富有挑戰性的問題情境，讓學生觀察、比較，引導學生合理地猜想。如，在教學《長方形的周長》中，筆者將一道普通的練習題改編成一道開放題：已知長方形的周長是20厘米，長與寬分別可能是多少厘米？請你拿出練習紙試一試。

就因為這么一改，一個與學生實際水平相適應的開放性、探索性問題就產生了，也就是這樣小小的一改，就為學生創設了富有挑戰性的問題情境，啟迪了學生的猜想：每種情況可能是一個怎樣的長方形呢？教學過程也因此發生了質的變化。

三、營造寬松環境，敢于猜想

心理學研究表明，良好的情緒能使學生的精神振奮，不良的情緒則會抑制學生的智力活動。另外，小學生的猜想能力受思維發展特點和自身現有知識的限制，再加上猜想的跳躍性，其結果必定存在著正確和錯誤之分。教師要堅持一條信念：允許“錯誤”，善待“錯誤”。久而久之，學生就不會有所顧慮，遇到新問題時便敢于猜想。如，在教學《長方形的周長》中，筆者讓學生猜想：“每種情況可能是一個怎樣的長方形？”同時，又用多媒體課件如下圖直觀地展現于學生的眼前。

如此，為學生創設了一種民主、和諧、平等、寬松的思考、交流、學習氛圍，學生身心放松，思維活躍，敢于猜想，敢于提出問題，敢于提出不同見解，敢于質疑，敢于挑戰，讓學生真正做到暢所欲言。只有這樣，學生創造性思維的火花才能迸發出來，各種奇思異想及眾多的“偏才”“怪才”才會在教師的贊許聲中不斷涌現出來。

四、搭建拓展舞臺，大膽猜想

著名數學教育家波利亞說：“讓我們大膽地教猜想！”的確，猜想是通向創新的康莊大道，我們教師應該特別關注學生建構知識的過程，努力挖掘創新支點，給學生提供充分的再創造，即創新的機會，培養學生的合情推理能力，培養學生的創新意識。如，《長方形的周長》最后一個環節的片段：

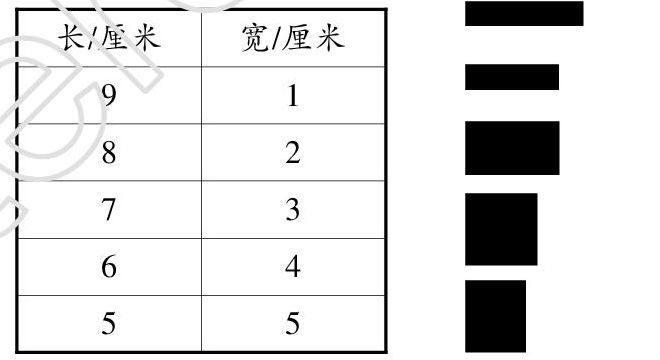
師：猜想一下，周長是幾厘米時，也能像剛才那樣出現正方形？邊長是幾厘米呢？……這樣的數說得完嗎？

最后形成板書：

師：你有什么發現嗎？

生1：豎著看，正方形的周長是邊長的4倍。

生2：橫著看，正方形的周長越來越大，邊長也越來越大。

生3：是的，是的，而且正方形的周長是加4加4的，邊長是加1加1的。

生4：邊長乘4就是正方形的周長。

……

數學猜想就是依據某些已知事實和數學知識，對未知量及其關系所做的一種推斷，是數學中的合情推理。所以，筆者根據正方形是特殊的長方形，讓學生大膽地進行猜想、發現和再創造正方形的計算方法，學生不僅能體驗到猜想和發現的樂趣，獲得積極的情感體驗，更重要的是能為學生今后真正的創新打下堅實的基礎。

猜想，是發現的起點，是探索的動力；猜想，是一種思維方式，是一種體驗過程，是一種學習方法……縱觀數學發展史，很多的數學結論都是從猜想開始的。因此，教師在平常的教學活動中，要充分鉆研教材，對教材中的猜想因素進行深入挖掘，根據班級實際，引導學生進行大膽猜想，嚴格論證，讓學生能在學到知識的同時，領悟到數學的方法，使學生的主體意識和創新意識在猜想中得到發展，這是我們每位教師義不容辭的職責。

參考文獻：

[1]波利亞.數學與猜想.科學出版社，1984.

[2]鄭金宗.談學生數學思維能力的培養.小學數學教育，2005（7/8）.

（作者單位 浙江省江山市文溪實驗學校）