談直線與平面垂直判定定理的教學

徐芬

高中數學立體幾何新教材體系中，有的概念直接運用公理來定義概念的教學方法，被教材和廣大教師所默認。最近，在一堂“直線與平面垂直的判定”公開課后，我們數學教研組對以此課中涉及到的公理定義概念及后續的判定定理的教學問題，進行了研究與討論，現整理如下，與同行一起探討。

一、運用公理定義“直線與平面垂直”概念的思考

對于直線與平面垂直定義的教學，大多教師會演示課本上的實例，旗桿與地面的位置關系，讓學生觀察直立于地面的旗桿及它在地面上的影子。并指出旗桿所在的直線與地面內任意一條過交點的直線垂直（和不過交點的直線也垂直）。

有些教師也會借助于使用多媒體CAI，展示在現實世界中大量存在的直線與平面位置關系中的這種很特殊的情形，對學生增強直觀的直線與平面垂直形象課堂容量進行演示。

在教師的誘導下，學生會利用知識的遷移，自然而然聯想到平面內兩條直線互相垂直和空間兩條直線相互垂直的知識，猜想總結出這種特殊位置關系應該稱為“直線與平面垂直”關系。此時，有的教師認為下定義的時機已經成熟，或者引導學生自己去給出準確的定義，或者直接給出教材中的概念：“一條直線和平面內的任何一條直線都垂直，我們就說這條直線和這個平面互相垂直”。我們研討認為這種教學方法有值得思考的地方。

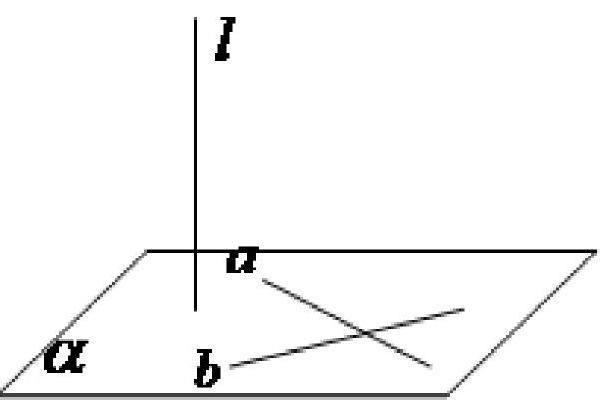
是不是我們一定要用“如果一條直線與平面內的所有直線都垂直則稱這條直線與平面垂直”來定義？當然我們也可用“如果一條直線與平面內的兩條相交直線垂直，則稱這條線與平面垂直”來加以定義（如圖）。我們知道，這里的兩種不同的條件實際上是等價的，可以互相推出，所以本來這兩種選擇都可以作為定義的。

既然二種關系原來都可以定義概念，那我們為什么要用第一種方法來定義？

在數學體系中，各個名詞是預先已經用公理定義的概念，這樣的公理系統是一個實質性公理系統。因為要先定義概念，所以就要有一些原始的概念作為定義其他概念的出發點。一般來說當幾種公理都可作為定義某一要領時，特別是有的概念在下定義時，本來就可以有多種選擇的情況下，數學體系中往往會把簡單的公理留著作為判定定理。比如在初中教材中，平行線的定義與判定定理就是如此。在此，我們就容易理解了數學體系中用第一種方法來定義直線與平面垂直概念，而不是用第二種方法來定義直線與平面垂直概念的理由了。

通過我們以上的教學，讓我們的學生知道了“如果一條直線與平面內的所有直線都垂直則稱這條直線與平面垂直”與“如果一條直線與平面內的兩條相交直線垂直，則稱這條線與平面垂直”從本質上來說是等價的道理，為后面的判定定理的學習與運用，埋下了伏筆。

二、從定義引入到判定定理教學的思考

接下來，我們再思考另一個問題，就是在學了“直線與平面垂直定義”后，如何引入“直線與平面垂直的判定定理”的問題？大多教師會按照教材的思路進行這樣的引入教學：“要證明一條直線和一個平面垂直，若每次都要證明這條直線和平面上每一條直線都垂直，顯然是很麻煩也不必要的”。

這樣的引入值得我們教師進行認真的思考了，注意這里教師的引導語“很麻煩也不必要”可能會給學生帶來二個誤處。

誤處一：“很麻煩”導致學生在不善于直接從定義去思考問題，

誤處二：“不必要”導致學生誤認為遇到有關直線與平面垂直的判定問題時，根本不用去想用定義去證明。

這種誤處，學生一旦形成，對所有的定義的理解和運用，特別是對學生的思維活動是非常有害的制約。

實際上，有許許多多的題，完全可以應用定義判定直線與平面垂直，例如：“如果兩條平行直線中的一條垂直于一個平面，那么另一條也垂直于同一個平面”，既可以用后面的判定定理證明，也可以用定義來證明。我們也可以運用定義來發散思維證題，例如：根據直線與平面垂直的定義，如果平面內存在一條直線與平面的一條交線b不垂直，則可以斷定此平面與直線b不垂直。

所以說，定義不是沒有用，而是看我們怎么去用。有時用定義去判定比用判定定理更容易解決問題。但大多數情況下，用定義去判定直線與平面垂直確實非常困難，要告訴學生，因為平面內直線的無限性，一條直線與平面內的所有直線都要判定與此垂直，既不現實，也難以操作，所以必須去尋找一種能夠避免逐一確定無限條直線與此直線垂直的問題，從而引入到判定定理的教學中。

三、對教材中的判定定理的思考

對直線與平面垂直判定定理，過去大多教師會這樣引入：“讓我們先來看看木工師傅是如何判斷一根立柱是否和板面垂直的方法，用曲尺（注：曲尺，是指木工及鉗工常用的一邊長一邊短的直角尺）檢查兩次，只要兩次，但曲尺靠板面的尺，兩次不能在同一條直線上，如果立柱、板面都和曲尺的兩條邊完全吻合，便可斷定立柱和板面垂直。從中你能得到判定直線和平面垂直的方法嗎？”引導學生進行猜想推測，從而引入判定定理。

有的教師也會按照教材P65圖2.3-4探究的折紙方法引入直線與平面垂直判定定理。但教材也好，老師也好，不管怎么引入判定定理，最后都沒有給予確切的嚴格證明，教材中只提出了二個思考問題作為運用時必須注意的問題——定理中兩條相交直線不可忽視（P65），就算把判定定理概念教學告一段落，接下去就直接進行如何運用判定定理了。

這種沒有嚴格證明的“判定定理”，我們認為教材處理不妥會讓學生有些迷茫。迷茫有三：

1.我們說，數學中的命題，必須經過嚴格的證明是正確的，才能成為定理。如果象教材上的實例引入，確實是對的，那也只是是用實驗的方法驗證了這確實是“正確”的。這種沒有經過嚴格證明的“判定定理”真的是正確的嗎？

2.剛剛前面說過，用定義判定直線與平面垂直不現實也難操作，所以要引入容易判定的直線與平面垂直的判定定理，而現在引入了判定定理卻又不給證明，這“判定定理”到底是對還是錯？

3.教師說，這定理以后可以借助空間向量等方法怎么怎么地來證明，如果以后確實可以證明了，那繞了一大圈，學生會不會說原來也可能是個數學怪圈？是否會產生循環論證之類的錯誤呢？用今天尚未證明的“判定定理”A推出B，再用B去推出C……，C推出A。

4.就算以后能證明是對的，又有多少學生以后會有這種機會和興趣去證明？學生此時的知識求知和探索科學的欲望將得不到滿足。

我們說，定理包括判定定理，只有從真命題（公理或其他已被證明的定理）出發，經過受邏輯限制的演繹推導，證明為正確的結論的命題或公式，才能成為定理。定理能描述事物之間內在關系，具有內在的嚴密性，不能存在邏輯矛盾。證明定理是我們數學教學的中心活動，那些相信為真但未被證明的數學只能敘述為猜想，不完全地歸納充其量只能是猜想而非定理。

（責任編輯 易 凡）