初中數學課堂中的“發現”教學

黃金松

摘 要： 在數學課堂教學中教師注重對學生“發現”意識的培養，有利于提高學生學習的積極性，有利于發展學生的智力。作者結合自己的教學實踐談談對“發現”教學的認識。

關鍵詞： 類比發現 歸納發現 直觀發現 學習遷移發現 探索發現

數學的形式化體系是建立在嚴格演繹推理的基礎上的。但是數學中許多定理，結論及其證明往往靠似真推理才得以發現。在數學教學中許多概念、原理或解題方法，與其老師竭盡全力講解，倒不如創造條件讓學生自己去探索發現更有效。在課堂教學中，教師隨時注意對學生“發現”意識的培養，有利于提高學生學習的積極性，有利于發展學生的智力。下面筆者結合自己的教學實踐，就“發現”教學談談自己的認識。

一、類比發現

在數學中許多創造發現首先是通過類比設問這一手段得到的。把新知識和舊知識進行類比，發現它們的共同特點和規律，提出猜想和判斷進行發現。

例如：在學習“分式的通分”教學時，可把它與分數通分相類比。先讓學生練習數的通分，讓其感覺到數的通分關鍵在于尋找分母的最小公倍數，引導學生把分數的通分規律運用到分式的通分中，尋找分式分母的最簡公分母。

又例如：在引入平面直角坐標系時，可以把它和數軸相類比。先復習數軸的有關知識，并指出數軸上的點可以用實數表示。再根據實例，從一維過渡到二維，提問：“用什么方法來表示平面內點的位置呢？”從而引進平面直角坐標系的概念。在數軸上的一個點，只需要一個實數來表示，而直角坐標系內的點需要用一對有序實數來表示。數軸上的點與實數一一對應，通過類比發現：平面直角坐標系內的點與有序實數對也有一一對應關系。

二、歸納發現

思維發展總是由具體到抽象，從個別到一般，從簡單到復雜。歸納可以幫助我們發現規律。在教學中，讓學生分析和比較某些單個的，特殊事物，從中發現規律性的東西，從而提出猜想，作出假設。

例如：在教學“同底數冪相乘法則”時，從四個層次設計問題：①底數、指數都是數字；②底數是字母，指數是數字；③底數是數字，指數為字母；④底數、指數都是字母。這樣的法則得出過程中，以相應的數學思想方法為主線，形成一個循序漸進的、具有內在聯系的問題體系，讓學生從特殊到一般，具體到抽象，通過分析、歸納發現規律。然后進行嚴格的邏輯論證得出法則。

又例如：在“數據的收集與處理”這一章的教學中，學生通過自主活動，從而歸納出調查、收集、處理數據的關鍵步驟，并能切實體會到普查與抽樣調查的區別。

三、直觀發現

數學形式過程大量源于直觀思維的結果。因此，在數學教學中不僅要培養學生的邏輯思維能力，還要培養直覺思維能力。充分利用學生的視覺作用，通過觀察圖形變化規律，提出假設進行發現。

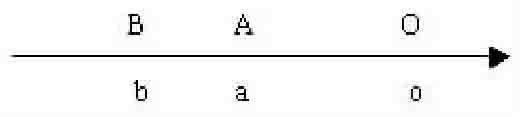
例如：在“兩個負數比較大小時，絕對值大的反而小，絕對值小的反而大”教學時可以先畫圖：

從數軸上看，A點在B點的右邊，所以a>b，A點離O點的距離比B點離O點的距離小，所以|a|<|b|，從而發現了兩個負數的比較法則。

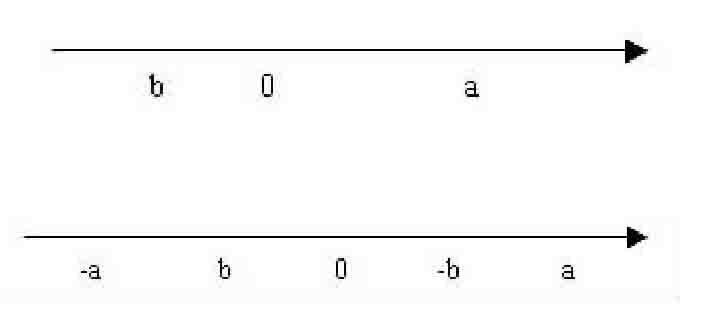
在遇到上述具體題目時，用數軸進行研究，使學生很快發現解題思路。例如：“如果a>0，b<0，a+b>0，把a，b，-a，-b四個數按大小順序用‘<號連接起來”，可以把已知條件體現在數軸上：

在數軸上分別找出a，b兩數的相反數所表示的點：

即發現其結論：-a

四、學習遷移發現

課堂教學過程的實質是教師引導學生運用原有的認知結構探求新知識的一個系統過程，利用學生已有的知識理解所需要學的新知識，運用教學手段，創設情境，引導學生學習遷移，進行發現。

例如：在“二元一次方程組和三元一次方程組解法”的教學中，可抓住消元設計遷移練習，由解二元一次方程組的基本思想，猜出解三元一次方程組的基本思想，從而發現三元一次方程組的一般解法。

五、探索發現

在課堂教學中，引導學生探索和研究所學新知識的已知條件，逐步深入，推導出未知的結論，從而進行發現。在“探索三角形全等的條件”和“探索三角形相似的條件”教學時，采用此手段，收到了事半功倍的效果。

以上是我在教學中的初步嘗試，收到了較好的效果。因此“發現”教學具有“舊中蘊新，新舊相融”的特點，使學生看到新知識后，自然“一見如故”，在課堂教學中充分發揮教師的主導作用和學生的主體作用，從根本上擺脫“注入式教學法”。當然，培養學生“發現意識”的途徑是多種多樣的，這還有待廣大教師作進一步研究。