奇妙的四色問題

田翔仁

繪制地圖，除了要求保證其準確性外，如何給地圖著色，從而能明顯地區分地圖上的各個區域，也是十分重要的. 很早以前，繪圖員就發現，只要配置幾種顏色就可以給任何地圖著色了. 究竟最少要用幾種顏色呢？這成了數學家們十分感興趣的問題.

四色問題的提出

相傳，四色問題是由英國青年數學家格思里提出來的. 1852年，他在繪制地圖時發現，給相鄰地區涂上不同顏色，只要四種顏色就足夠了. 他把這個發現告訴了在大學讀書的弟弟. 他的弟弟便向英國數學家摩根請教，摩根又向著名數學家哈密頓請教，但是，問題仍然沒有解決……

1878年，英國數學家凱萊正式向倫敦數學學會提出這個問題，這才引起了數學界的重視. 世界上許多數學家爭相進行研究，其中有數學家肯普、希伍德、閔可夫斯基等，結果仍然一無所獲. 人們開始認識到，這貌似簡單的題目，其實是一道超級數學難題.

四色問題的證明

進入20世紀后，證明四色問題的研究才逐漸取得進展. 1913年，美國數學家伯克霍夫改進了肯普的方法，引進了一些新技巧，導致1939年美國數學家富蘭克林證明了22國以下的地圖可以只用四色著色. 1950年溫恩證明了35國，1968年奧爾又證明了39國，1975年有報道，已證明了52國.

為什么進展如此緩慢？主要是由于數學家提出的檢驗方法太復雜，工作量太繁重. 一直到1976年，美國數學家阿佩爾和哈肯利用計算機工作了1200小時，作了100億個判斷，終于證明了四色問題是正確的. 這是人類首次依靠計算機的幫助解決了著名的數學難題.

點、線、面的關系

隨意畫曲線的涂鴉之作也能體現數學的趣味性.

下面有一條隨意畫的連續曲線，起點和終點分開，我們可以用三種顏色，把它們的各個區域涂上不同的顏色.

下面我們先動手把這張地圖填上顏色，再研究一下幾個數量.

1. 頂點與交叉點的個數（V）；

2. 連接兩點的曲線段的數量（E）；

3. 包括底圖在內的所有大小區域的數量（F）.

看看這三個數量之間有什么關系.

統計結果是：點數為10，線數為17，面數為9，然后得出10+9=17+2.

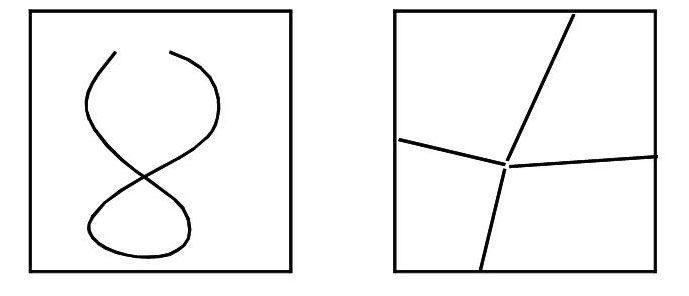
如果我們再分析下面兩張特殊的地圖：

它們之間都滿足這樣的關系，即點數+面數=線數+2.

即V+F=E+2，這個關系式稱為歐拉公式.

給點涂色

這里有一個圖形，上面有若干個頂點（交叉點）. 如果我們給這些點涂色，并要求任何一根線的兩個頂點的顏色不同，最少需要多少種顏色？

給線涂色

如果我們給這里的圖形和線段涂色，并要求相鄰的線段的顏色不同，最少需要多少種顏色？