顆粒尺寸分散度對顆粒體系力學和幾何結構特性的影響*

馮旭張國華 孫其誠

1)(北京科技大學物理系，北京 100083)

2)(清華大學，水沙科學與水利水電工程國家重點實驗室，北京 100084)

(2013年5月4日收到;2013年6月18日收到修改稿)

1 引言

近年來，無序材料的力學和幾何結構特性受到了較多關注.Silbert和Silbert[1]對比分析了三維無摩擦和有摩擦顆粒體系的靜態結構因子S(k)，發現光滑顆粒體系在雙對數坐標下S(k)曲線在低k區的線性行為，其斜率近似為1.Xu和Ching[2]研究了三維雙分散光滑顆粒體系中，發現靜態結構因子強烈的依賴顆粒粒徑比，以前發現的低k部分的S(k)～k僅僅是顆粒的粒徑比接近1時的特殊情況.

與此同時，關于二維體系力學和幾何結構特性的研究也取得了很大進展.Han等[3]研究了二維膠體晶體的取向序關聯函數，發現當處于Hexatic相-液相共存區時，系統的取向序關聯函數g6(r)～e-r/ξ6，且取向序關聯長度ξ6隨面密度ρ的變化規律與Kosterlitz-Thouless-Halperin-Nelson-Young理論的預測相符[4].Peng等[5]發現甚至當二維膠體晶體融化到液相時，取向序關聯g6(r)曲線仍然以指數方式衰減.

近年來，關于二維體系結構因子的研究也取得了很大進展.Meyer等[6]發現在中間波矢區域二維聚合物溶液結構因子隨k呈冪律標度S(k)～kν，且隨著鏈長度N的增加，冪律指數ν從-2變到-3.Wen等[7]發現二維顆粒鏈的靜態結構因子S(k)～k-2，與密集的聚合物溶液結構相似.

在本文中，我們用顆粒離散元法(DEM)生成了由2048個二維圓形顆粒、邊壁壓強為1000Pa的系統，為了研究顆粒尺寸分散度s對系統性質的影響，每個分散度下隨機生成100個位形.通過研究體系的配位數、剪切模量、靜態結構因子、取向序關聯、力的累積分布等物理量隨尺寸分散度的變化規律，進一步分析了體系的無序程度對二維顆粒體系力學和幾何結構特性造成的影響.

2 數值模擬

在2 m×2 m的正方形盒子里，隨機放置質量相等的2048個光滑圓盤顆粒，采用了周期性邊界條件.為了研究粒徑分散度s對系統力學性質的影響，顆粒半徑在范圍內等概率取值，其中d0=0.01 m為顆粒的平均直徑，s的取值范圍為[0，0.5].我們對每個粒徑分散度隨機生成100個壓強為1000 Pa的位形，本文所涉及的物理量都是這100個位形的統計平均值.文中，顆粒與顆粒相互作用為單邊線性彈簧，即當顆粒i和j間距rij=ri-rj小于它們的半徑之和時存在相互作用，其中ri，rj分別為顆粒i和j的位置矢量.接觸力的法向分量由Fnij=-knnij給出，其中kn是法向接觸剛度，nij=rij/|rij|.在本文的模擬中，顆粒法向剛度系數為1.0×106N/m，切向剛度系數為0，不考慮重力.

具體產生位形的過程如下：首先，我們在盒子中隨機產生2048個粒徑很小的多分散顆粒，此時顆粒間沒有任何重疊，體系處于松弛狀態.然后，在保持分散度固定的前提下使顆粒半徑增大，直至體系的體積分數達到0.88.最后，利用半徑減小的辦法卸載，使得體系達到目標壓強1000 Pa.其中，位形穩定的判據是經過1000個循環前后系統的能量差的比例小于1.0×10-15.

3 結果與分析

3.1 配位數和剪切模量

配位數是某一顆粒與周圍其他顆粒的接觸數目，它是表征系統幾何特征的重要物理量.為了研究尺寸分散度對系統幾何特征的影響，我們分析了平均配位數隨尺寸分散度的變化規律，如圖1(a)中所示.當s＜0.1時，平均配位數的值隨分散度的增加迅速減小;而當s＞0.1時，體系中顆粒的平均配位數趨于4.1，說明此時系統的尺寸無序程度對配位數基本沒有影響.

剪切模量是彈性材料承受τ剪應力與產生的γ剪應變的比值，是表征顆粒物質抗剪切能力的力學指標.圖1(b)是系統平均剪切模量隨尺寸分散度s的變化曲線.可以看出，平均剪切模量和平均配位數隨s的變化趨勢一致.圖1(c)給出了平均剪切模量隨平均配位數隨s的線性變化規律，〈Z〉=3.5+3.3×10-5·G.由圖 1(a)，(b)，(c)可以看出，s=0.1可能是個分界點：當體系的尺寸s＜0.1時，s越大(系統越無序)，系統的抗切應變能力越弱;而當s＞0.1時，系統的無序程度已經對其幾何和力學性質沒有任何影響.

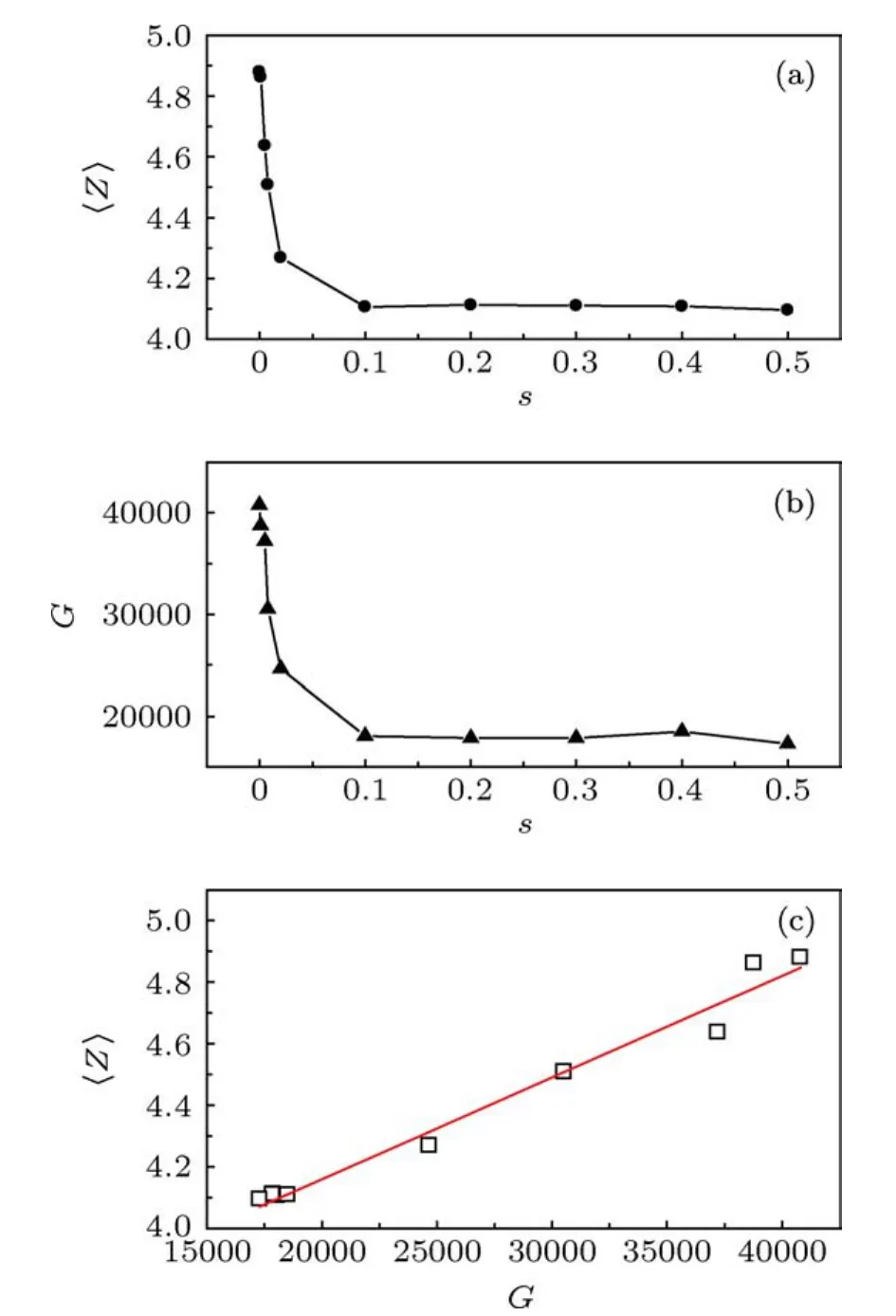
圖1 平均配位數〈Z〉，剪切模量G隨分散度s的變化及二者的線性關系 (a)〈Z〉隨s的變化;(b)G隨s的變化;(c)〈Z〉隨G的變化

3.2 靜態結構因子

靜態結構因子S(k)是表征顆粒體系細觀結構的典型參量[8-13]，定義為

我們模擬了s=0，0.001，0.005，0.008，0.02，0.1，0.2，0.3，0.4和0.5時的靜態結構因子，結果如圖2所示.可以看出，在高k區域，尺寸分散度s＜0.1的S(k)曲線基本重合，并且在k′=2kπ/L=45，80，90附近各出現一個尖銳峰.隨著s增大，峰值趨于平緩，而且在k′=80和k′=100附近這兩個峰逐漸合并成一個平滑的峰.在低k區域(k＜20)，當s＞0.1時，S(k)幾乎不隨k變化，S(k)的值隨著分散度的增大而增加;當s≤0.02時，二維體系的S(k)曲線在3＜k′＜5區域遵從冪律標度，S(k)～k-4/3，如圖2插圖所示.這一點符合二維線性聚合物鏈體系中在中間波矢范圍的標度關系，S(k)～k-1/υ，與文獻[6，7，15]的結果類似，這暗示著二維單分散體系中存在顆粒鏈結構.

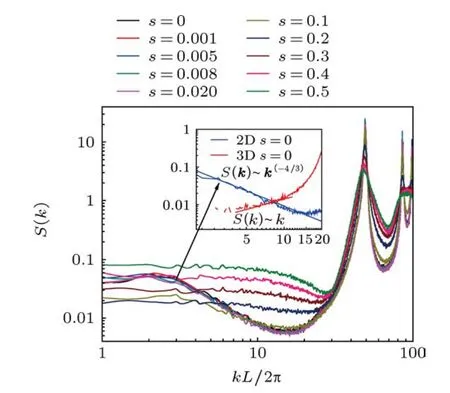
圖2 靜態結構因子S(k)隨k的變化，插圖為單分散體系下S(k)曲線低k部分數值擬合

為了研究維度對體系結構因子的影響，我們生成了由10000個球形顆粒組成、壓強為10-4Pa的三維單分散顆粒體系，并計算了其結構因子，如圖2插圖所示.可以發現，三維單分散體系的靜態結構因子在低k區域滿足：S(k)～k，與文獻[1]中的結論一致.造成二維和三維體系S(k)在低k區域不同的原因可能是，在二維體系中更容易形成長程關聯.

圖3為不同分散度下二維顆粒體系S(k)的云圖.可以看出，單分散體系(即s=0)表現出晶體的特征，其S(k)呈三角格子排列;而s=0.1的體系則表現出典型的多晶衍射圖樣的特征，衍射圖形呈現出明暗不均勻的同心圓環;隨著粒徑多分散度的增大，圖形中從中心開始的第二個圓環由正六邊形演變為圓形，圓環的徑向寬度也隨之增加，而且看不到明顯的點;當s≥0.3時，同心圓環變得更寬且彼此合并，其外圍輪廓逐漸變得模糊，表明系統隨著s的增大越來越無序;當s=0.5時，只能看到一個比較清晰的圓環.

3.3 取向序關聯

為了量化顆粒i的取向序，引入鍵取向序參數Ψ6i[16]：

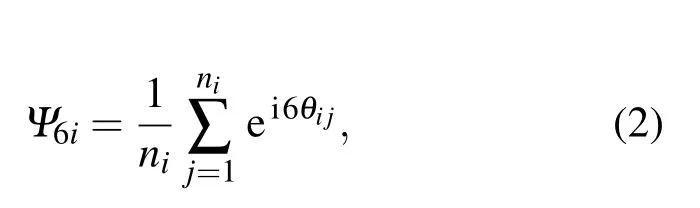
式中，ni表示顆粒i的最近鄰顆粒的數目，θij表示顆粒i和其近鄰顆粒j之間的極角.為了進一步量化取向序的空間關聯，本文計算了顆粒體系的取向序關聯函數g6(r)[3,17,18]，定義為

圖3 不同分散度下靜態結構因子S(k)

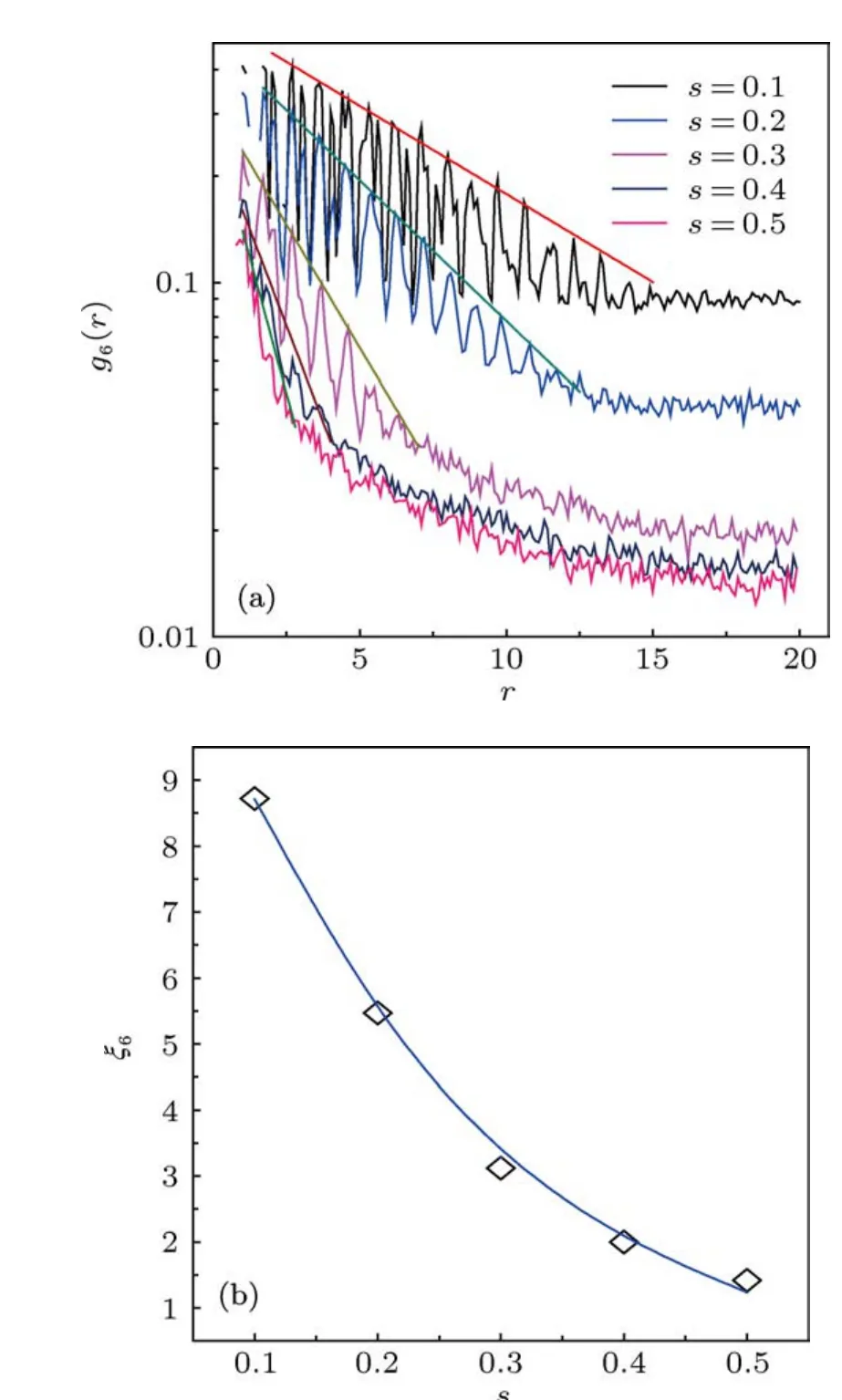
圖4 取向序關聯g6(r)隨r的變化及擬合參數ξ6隨分散度s的變化規律 (a)g6(r)隨r的變化;(b)ξ6隨s的變化;實線為ξ6∝14.2e-s/0.2

圖4(a)給出了不同分散度下的取向序關聯函數g6(r).由圖4(a)可知，取向序關聯函數呈現隨著r的增大幅值逐漸減小的振蕩行為.其中，g6(r)的極小可能與顆粒沒有占據晶格的位置有關，而g6(r)振蕩衰減的長度范圍則對應取向關聯的長度.為了得到取向序關聯長度，我們對曲線進行了e指數擬合，如圖4(a)所示.虛線為擬合曲線：g6(r)∝ae-r/ξ6，其中ξ6是序關聯長度.由圖4(a)可知，s＞0.1的g6(r)曲線均呈e指數衰減，表明s＞0.1的顆粒體系表現出與液體類似的短程序[3,19].圖4(b)給出了序關聯長度隨分散度變化的曲線，顯然，隨著s的增加序關聯長度近似以e指數規律衰減，如圖4(b)中的實線所示.總之，隨著粒徑分散度s增大，ξ6減小，而且減小的幅度越來越慢，變化比較連續.說明隨著粒徑多分散度s從0.1到0.5，體系越來越無序，而且它的變化并不是一個突變，而是一個結構連續變化的過程.此時，體系無序程度對顆粒間取向序關聯的影響比較明顯.

3.4 力的累積分布

在靜態顆粒排布中，顆粒間接觸力形成高度各向異性的力網絡，其基本特征可以用接觸力的概率密度函數p(f)表征，其中f=F/〈F〉為歸一化力.近年來，大量的實驗和模擬關注大f處p(f)的分布，由于實驗上的困難，對于小f處p(f)分布的研究還不是很多[20].我們計算了不同分散度下顆粒體系中的力累積分布G(f)，G(f)=圖5可以看出，當f＜2時，隨著f的增大，G(f)值也增大;當f＞2后，G(f)趨近于1.而且，不同分散度下的G(f)曲線幾乎重合，暗示系統的無序程度對力累積分布幾乎沒有影響.

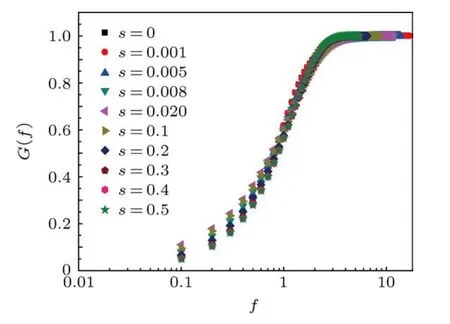
圖5 力的累積分布G(f)隨 f的變化

4 結論

采用顆粒離散元方法生成了具有不同尺寸分散度的二維顆粒體系，進一步研究了尺寸分散度對體系力學和幾何結構特征的影響，得到如下結論：1)二維顆粒體系，平均配位數和平均剪切模量隨著s的增大而減小;當s＞0.1時，二者都基本保持為定值，說明隨著s的增大，體系的無序程度增加;2)當分散度s≤0.02時，靜態結構因子低k部分的曲線基本重合;當s＞0.1時，隨著s的增大，S(k)的值也均勻增加，尤其是s=0時，二維顆粒體系S(k)的低k區域行為與聚合物顆粒鏈的類似，S(k)～k-1/υ(υ=3/4)，這一點不同于三維單分散顆粒體系(其S(k)曲線低k部分斜率近似等于1)，暗示二維單分散顆粒體系(包括分散度較小的體系)結構上與顆粒鏈相似;3)不同分散度下，取向序關聯函數g6(r)曲線的峰值均滿足e指數關系，序關聯長度ξ6也隨尺寸分散度的增大而減小;4)力的累積分布G(f)不隨尺寸分散度的變化而變化，說明它基本不受系統無序程度的影響.

[1]Silbert L E，Silbert M 2009Phys.Rev.E 80 041304

[2]Xu N，Ching E S C 2010Soft Matter6 2944

[3]Han Y，Ha N Y，Alsayed A M，Yodh A G 2008Phys.Rev.E 77 041406

[4]Artoni R，Santomaso A C，Gabrieli F，Tono D，Cola S 2013Phys.Rev.E 87 032205

[5]Peng Y，Wang Z，Alsayed A M，Yodh A G，Han Y 2010Phys.Rev.Lett.104 205703

[6]Meyer H，Schulmann N，Zabel J E，Wittmer J P 2011Comput.Phys.Commun.182 1949

[7]Wen P P，Zheng N，Li L S，Li H，Sun G，Shi Q F 2012Phys.Rev.E 85 031301

[8]Yang J K，Schreck C，Noh H，Liew S F，Guy M I，O’Hern C S，Cao H 2010Phys.Rev.A 82 053838

[9]Xu W S，Sun Z Y，An L J 2012J.Chem.Phys.137 104509

[10]Berthier L，Chaudhuri P，Coulais C，Dauchot O，Sollich P 2011Phys.Rev.Lett.106 120601

[11]Paulus M，Gutt C，Tolan M 2008Phys.Rev.B 78 235419

[12]Donev A，Stillinger F H，Torquato S 2005Phys.Rev.Lett.95 090604

[13]Torquato S，Stillinger F H 2003Phys.Rev.E 68 041113

[14]Warr S，Hansen J P 1996Europhys.Lett.36 589

[15]Maier B，R¨adler J O 1999Phys.Rev.Lett.82 1911

[16]Schreck C F，O’Hern C S，Silbert L E 2011Phys.Rev.E 84 011305

[17]Agarwal U，Escobedo F A 2012Soft Matter8 5916

[18]Prestipino S，Saija F，Giaquinta P V 2011Phys.Rev.Lett.106 235701

[19]Bakker A F，Bruin C，Hilhorst H J 1984Phys.Rev.Lett.52 449

[20]Charbonneau P，Corwin E I，Parisi G，Zamponi F 2012Phys.Rev.Lett.109 205501