多孔材料彈性模量預(yù)測的數(shù)值方法
顧 政,鄭建軍,周欣竹
(浙江工業(yè)大學(xué)建筑工程學(xué)院,杭州 310014)
多孔材料普遍存在于自然界中,木材、生物的骨骼以及巖石等都是天然的多孔材料。隨著科學(xué)技術(shù)的發(fā)展,出現(xiàn)了越來越多用金屬、陶瓷和高聚合物等制成的人造多孔材料[1]。這些多孔材料已廣泛應(yīng)用于各個工程領(lǐng)域,它們不僅具有多種優(yōu)異的性能,而且制造工藝簡單。因此,研究其力學(xué)性能具有突出的重要性。
由于多孔材料是由孔隙和固相所組成的復(fù)合體,孔結(jié)構(gòu)(如孔形狀、孔隙率和孔的連通性等)是影響宏觀彈性性能的主要因素,因而細觀結(jié)構(gòu)與宏觀力學(xué)性能之間的定量關(guān)系成為當(dāng)前國際工程界的前沿課題之一。Voigt和Reuss分別根據(jù)等應(yīng)變和等應(yīng)力假設(shè)給出了多晶體材料體積模量和剪切模量的近似解[2],Gibson和Ashby[3]在單孔單元的基礎(chǔ)上建立模型,獲得了蜂窩多孔材料二維彈性參數(shù),即Gibson-Ashby方程,Roberts[4]研究了開孔和閉孔泡沫的彈性性能。隨著數(shù)值方法和計算機技術(shù)的日益發(fā)展,有限元法被廣泛用于多孔材料的力學(xué)性能分析[5],對“代表性體積元”進行數(shù)值求解,獲得宏觀力學(xué)性能。但對于復(fù)雜的多孔材料,不僅網(wǎng)格劃分極其困難,總剛度矩陣占據(jù)大量內(nèi)存,而且總剛度方程求解花費大量時間,以至于無法獲得滿意的數(shù)值解。為此,該文在前人工作的基礎(chǔ)上,應(yīng)用快速傅里葉變換法討論了多孔材料彈性模量的計算方法。
1 數(shù)值方法
1.1 多孔材料模擬
類似于“代表性體積元”,可以從細觀結(jié)構(gòu)圖像的像素點上獲得結(jié)構(gòu)單元的代表性信息[6]。因而為了能較準確地預(yù)測多孔材料的彈性模量,首先應(yīng)建立多孔材料模型,作為初步嘗試,文章僅考慮二維模型。多孔材料區(qū)別于普通密實固體材料的最顯著特點是具有孔隙,多孔材料建模時應(yīng)著重考慮孔隙分布特點以及孔隙率大小。大量的試驗研究表明[7],多孔材料中的孔隙率、孔徑分布、孔隙位置等均服從一定的統(tǒng)計分布規(guī)律,如隨機分布和正態(tài)分布等。因此,建立多孔材料幾何模型的關(guān)鍵是按照一定的概率分布確定孔隙大小和位置,在數(shù)學(xué)上可以通過各種變換或抽樣來實現(xiàn)。
為了便于計算,該文假設(shè)孔隙為圓形,而且大小相等、互不重疊。在模擬孔隙時,先選取一邊長為L的正方形,在分布第i個半徑為R的圓孔時,在正方形區(qū)域內(nèi)生成其圓心坐標(xi,yi),如果第i個圓孔與前面已經(jīng)分布某一個或幾個圓孔重疊,則重新生成第i個圓孔的圓心坐標;如果第i個圓孔不與前面已經(jīng)分布的(i-1)個圓孔重疊,那么繼續(xù)分布第i+1個圓孔,直到達到給定的孔隙率為止。作為一個算例,設(shè)L=100mm,R=4mm,孔隙率C分別為0.1、0.3和0.5,所獲得的孔分布如圖1所示。
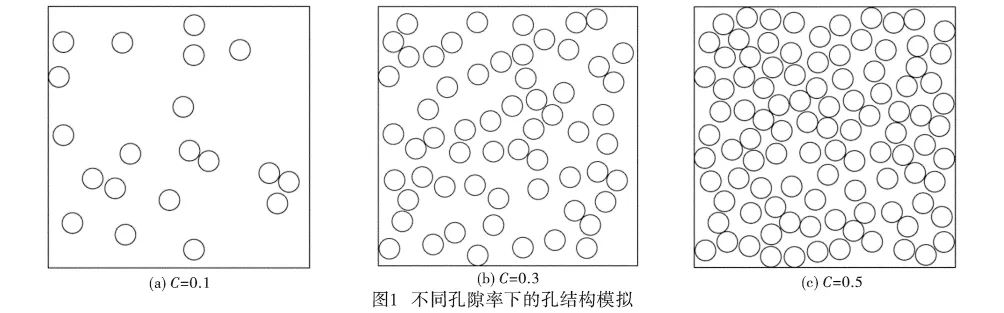
1.2 基本方程
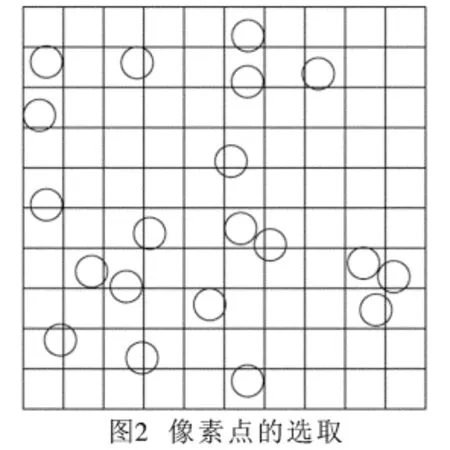
首先在模擬區(qū)域內(nèi)等距離選取像素點,根據(jù)快速傅里葉變換原理,每個二維細觀結(jié)構(gòu)分布圖都包含2K×2K個像素點,這些像素點各自具有力學(xué)性質(zhì),且相互獨立,計算步驟如下:
1)將圖像劃分為2K×2K個細胞單元,如圖2所示,取每個細胞單元的中心點為像素點,這里稱K為像素點個數(shù)指數(shù)。
2)對每個像素點進行判斷,如果落在孔隙內(nèi),彈性模量取為零;如果落在固相內(nèi),彈性模量取單位值,這樣所獲得的多孔材料的彈性模量為相對值。
多孔材料各點的彈性張量Cijkl(x)是坐標x的函數(shù),其應(yīng)力-應(yīng)變關(guān)系可表示成

式中,C0ijkl為彈性張量常數(shù),τij(x)定義為
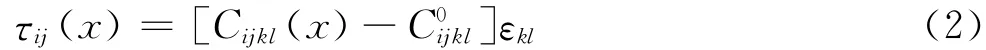
通過引入周期性格林張量Γijkl,式(1)的解可表示為[6]

對式(3)進行傅里葉變換有

對于各向同性材料,(ξ)為[6]
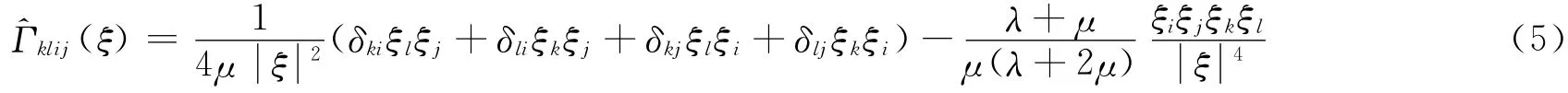
式中,λ和μ為拉梅常數(shù),εi為傅里葉空間坐標。
1.3 迭代求解
方程(1)~方程(4)可以通過以下迭代方法進行求解:
1)給定初始均勻應(yīng)變ε0ij,由式(1)求得初值應(yīng)力σ0ij;
2)對于第i+1次迭代,先由(2)計算τij(x),對τij(x)進行傅里葉變換求得^τij(ξ),再檢驗收斂性;
3)由式(4)計算第i+1次迭代應(yīng)變,再將應(yīng)變進行傅里葉反變換;
4)由式(1)計算應(yīng)力。
一旦迭代收斂,計算各點的加權(quán)應(yīng)力和加權(quán)應(yīng)變,最后獲得多孔材料的彈性模量。該文以前后兩次迭代值的相對誤差小于10-3作為收斂準則。
2 收斂性和有效性驗證
2.1 收斂性驗證
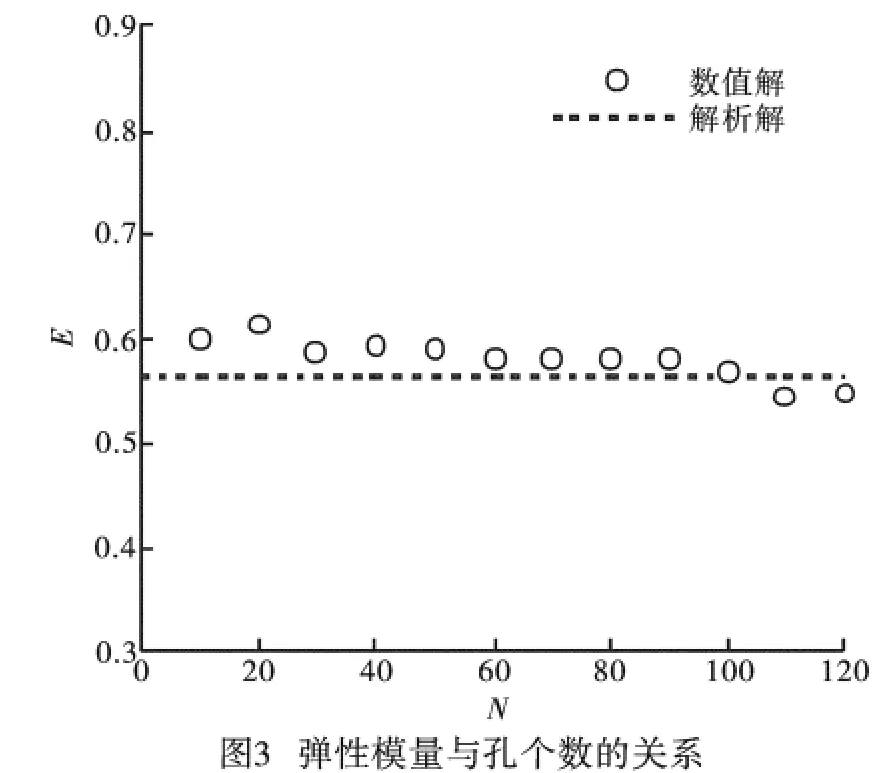
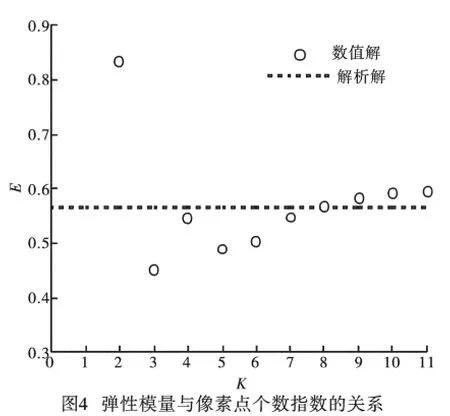
在下面的計算中,取正方形邊長為1 000mm,孔隙率C=0.2,像素點個數(shù)為28×28個,固相材料的泊松比為0.3,計算所得的相對彈性模量與孔隙個數(shù)之間的關(guān)系如圖3所示,其中,虛線表示解析解[8]。從該圖可以看出,當(dāng)孔隙個數(shù)較少時,彈性模量上下波動,當(dāng)孔隙數(shù)大于100時,彈性模量基本趨于穩(wěn)定,這與文獻[9]的結(jié)論一致,這是因為孔隙越多,材料越均勻,像素點所代表的結(jié)構(gòu)單元性質(zhì)越接近于真實情況。再取孔隙個數(shù)為100,相對彈性模量與像素點個數(shù)指數(shù)之間的關(guān)系如圖4所示。從該圖可以看出,當(dāng)K較小時,彈性模量上下波動幅度較大,隨著K的增大,結(jié)果趨于穩(wěn)定,K=10與K=11之間彈性模量的相對誤差僅為0.3%,表明該方法已經(jīng)收斂。圖4還表示,隨著像素點的增加,數(shù)值解與解析解越接近,這是因為隨著像素點的增加,結(jié)構(gòu)單元性質(zhì)得到更細致的描述,更接近于真實情況,另一方面,由于傅里葉變換本身具有一定的誤差,當(dāng)像素點超過一定值后,累積誤差也會影響計算結(jié)果。由圖4還可以得出,當(dāng)像素點個數(shù)為256×256時,數(shù)值解與解析解最接近。
2.2 有效性性驗證
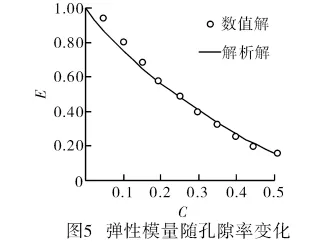
基于前面的討論,取孔隙個數(shù)為100,像素點個數(shù)為256×256,相對彈性模量隨孔隙率變化如圖5所示。從圖5可以看出,數(shù)值解與解析解良好吻合,當(dāng)孔隙率為0.10、0.20、0.30、0.40和0.50時,兩者之間的誤差分別為6.70%、1.17%、2.12%、3.36%和7.03%,其平均值為4.37%。因此,文中方法的有效性得到初步證實。
3 結(jié) 論
a.基于Moulinec和Suquet所提出的快速傅里葉變換法,討論了多孔材料彈性模量計算,通過與文獻中的解析解比較,初步證實了該數(shù)值方法的有效性。
b.定量評價了孔隙個數(shù)和像素點個數(shù)對計算結(jié)果的影響,發(fā)現(xiàn)多孔材料越均勻、像素點個數(shù)越多,數(shù)值解越精確。
[1] 劉培生.多孔材料引論[M].北京:清華大學(xué)出版社,2004.
[2] Torquato S.Random Heterogenerous Materials:Microstructure and Macroscopic Properties[M].New York:Springerverlag,2001.
[3] Gibson L J,Ashby M F.Cellular Solids:Structure and Properties[M].Cambridge:Cambridge University Press,1997.
[4] Roberts A P,Garboczi E J.Elastic moduli of model random three-dimensional closed-cell cellular solids[J].Acta materialia,2001,49(2):189-197.
[5] Bardenhagena S G,Brydona A D,Guilkey J E.Insight into the physics of foam densification via numerical simulation[J].Journal of the Mechanics and Physics of Solids,2005,53(3):597-617.
[6] Moulinec H,Suquet P.A Numerical Method for Computing the Overall Response of Nonlinear Composites with Complex Microstructure[J].Computer Methods in Applied Mechanics and Engineering,1998,157(1-2):69-94.
[7] 鞠 楊,楊永明,宋振鐸,等.巖石孔隙結(jié)構(gòu)的統(tǒng)計模型[J].中國科學(xué)E輯,2008,38(7):1026-1041.
[8] Zheng Q S,Hwang K C.Two-dimensional Elastic Compliances of Materials with Holes and Microcracks[J].Proceedings of the Royal Society of London,1997,453(1957):353-364.
[9] Hu N,Wang B,Tan G W,et al.Effective Elastic Properties of 2-D Solids with Circular Holes:Numerical Simulations[J].Composites Science and Technology,2000,60(9):1811-1823.

