解線性不等式約束凸規(guī)劃問題的勢下降內(nèi)點算法

張 濤,陳 忠,呂一兵

(長江大學信息與數(shù)學學院,湖北 荊州 434023)

解線性不等式約束凸規(guī)劃問題的勢下降內(nèi)點算法

張 濤,陳 忠,呂一兵

(長江大學信息與數(shù)學學院,湖北 荊州 434023)

提出了一種解線性不等式約束凸規(guī)劃問題的勢下降算法,并在一定的假設(shè)條件下,證明了該算法的收斂性,最后通過數(shù)值實驗驗證了該算法的有效性.

凸規(guī)劃;不等式約束;勢下降內(nèi)點算法

0 引 言

自1984年Karmarkar[1]提出了解線性規(guī)劃問題的內(nèi)點算法以來,一些學者運用線性規(guī)劃內(nèi)點算法的思路來求解凸規(guī)劃問題的Karmarkar內(nèi)點算法[2-4],但這些方法絕大部分是求解等式約束凸規(guī)劃問題.為此,基于Karmarkar內(nèi)點算法,本研究提出了一種求解線性不等式約束凸規(guī)劃問題的勢下降內(nèi)點算法,并證明了該算法的收斂性,最后通過具體算例驗證了該算法的有效性.

1 不等式約束的凸規(guī)劃模型

其中,A∈Am×n,b∈Rm,f(x)為開凸集D?Rn上的凸函數(shù),f(x)二階連續(xù)可微.

根據(jù)K-T條件,問題(1)的最優(yōu)性充要條件可表示為,

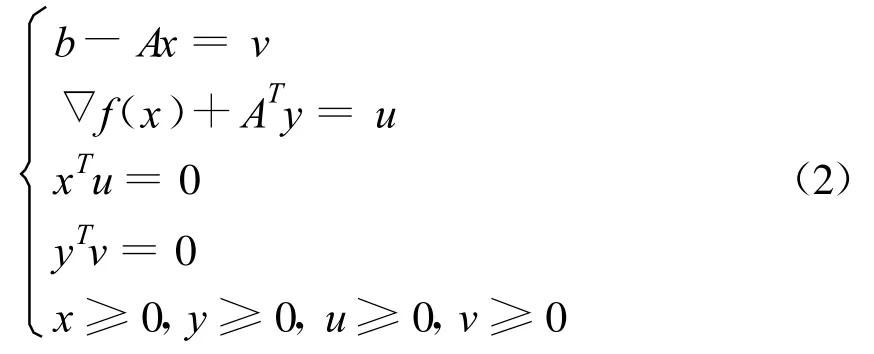
注意到,對z∈ Ω0有 g(z)＞0,z*滿足條件(2)當且僅當z*∈ Ω0且g(z*)=0,故定義如下勢函數(shù),

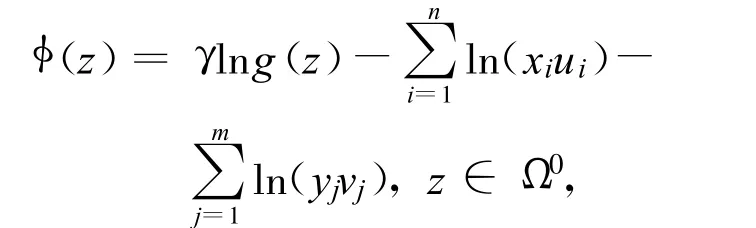
其中,γ＞n+m是任意給定的常數(shù).由算術(shù)—幾何平均不等式易知,

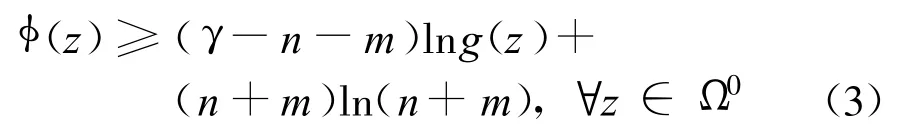
在迭代點zk處,取如下方程組的解作為搜索方向,

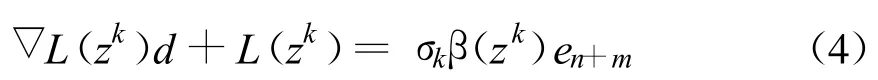
所有 z∈ Ω0,映射L(z)的Jacobi矩陣為,

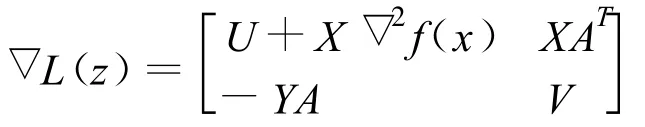
其中,X,Y,U和V分別是以向量x,y,u及v的元素為對角元的對角矩陣,▽2f(x)表示f的二階偏導組成的Hessian矩陣.對所有z∈ Ω0,線性方程組(4)都有唯一解,并可證明該唯一解是勢函數(shù)φ(z)在點z處的一個下降方向.

2 基本定理

引理1[5]如果C和D是正定對角陣,B是半正定的,則 C+DB是非奇異的.

定理1 對所有的z∈ Ω0,矩陣 ▽L(z)都是非奇異的.

證 對任意 z∈ Ω0,只需證明齊次方程組▽L(z)d=0的解d=(d1,d2)T為零.

由,

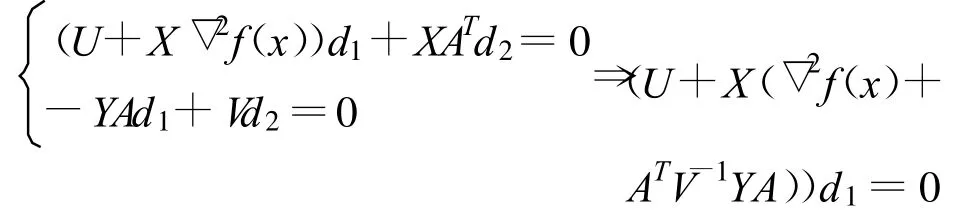
由于f(x)為開凸集D?Rn上的凸函數(shù)且二次連續(xù)可導,則 ▽2f(x)半正定,▽2f(x)+ATV-1YA是半正定的,由引理1,U+X(▽2f(x)+ATV-1YA)是非奇異的,故 d1=0,從而d2=0即 d=0,所以矩陣 ▽L(z)是非奇異的.

定理1表明,對所有的z∈ Ω0,方程組(4)都有唯一解.

下面證明,該唯一解還是勢函數(shù)φ(z)在點z處的一個下降方向.

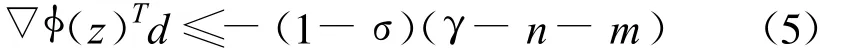
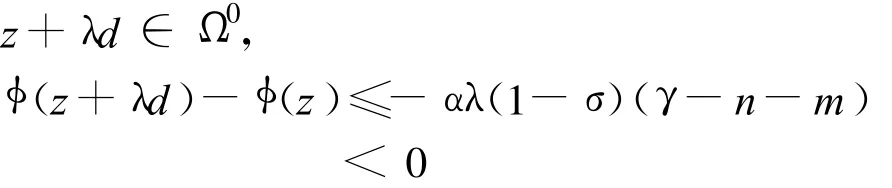
證 勢函數(shù)φ(z)在Ω0上是連續(xù)可微的,它在點z∈ Ω0處的梯度為,

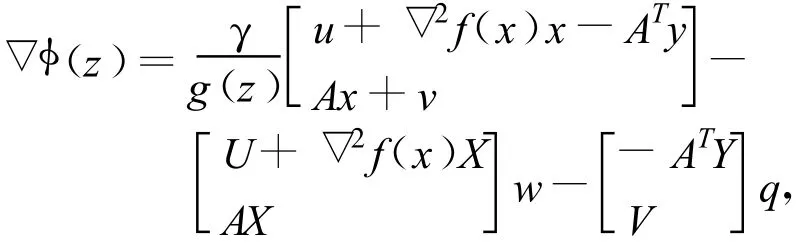
其中,

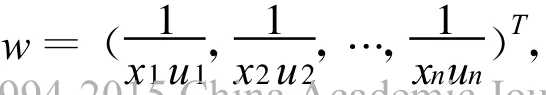
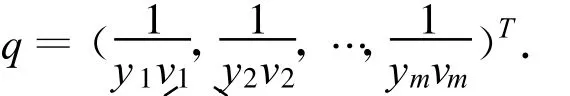
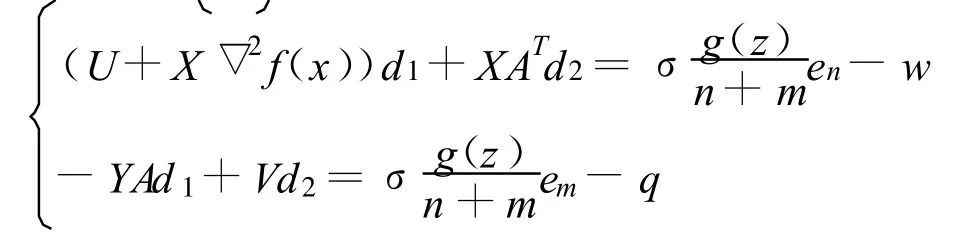
且滿足,

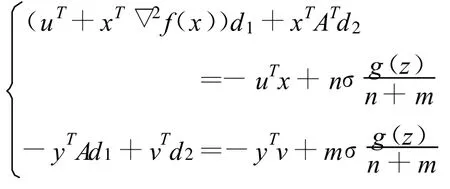
則,

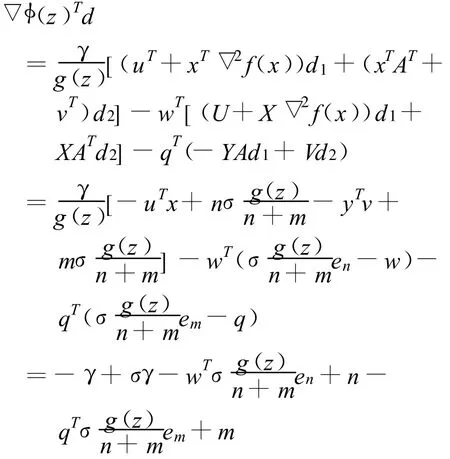
由算術(shù) —幾何平均不等式有,

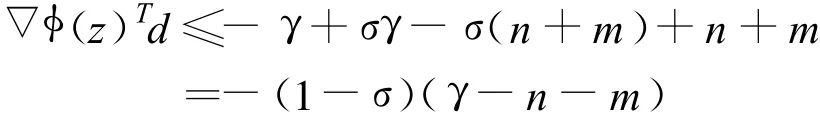
即(5)式成立.

3 勢下降內(nèi)點算法

3.1 勢下降內(nèi)點算法步驟

勢下降內(nèi)點算法的具體步驟為:

2)求解方程組 ▽L(zk)d+L(zk)=σkβ(zk)en+m,得搜索方向 dk;

3)令mk是滿足下面條件的最小非負整數(shù),zk+βρmdk∈ Ω0,φ(zk+βρmdk)- φ(zk) ≤-α βρm(1-σk)(γ-n-m),令 zk+1=zk+βρmdk;

4)檢驗zk+1是否滿足預先給定的終止條件:如果滿足,停止迭代;否則取 σk+1∈[0,],令 k=k+1并轉(zhuǎn)2).

3.2 算法收斂性分析

定理3 由勢下降內(nèi)點算法產(chǎn)生的迭代點列{zk}有界,其每個聚點都滿足條件(2)且對函數(shù)g(z)有

證 易知迭代點列{zk}有界.設(shè)z*是{zk}的任一聚點,則z*∈ Ω且存在{zk}的一個子序列,設(shè)為{zk:k∈K},使得zk→z*(k∈K),K為所有迭代數(shù)列.為證明z*滿足條件(2),只需證明g(z*)=0.

采用反證法,假設(shè)g(z*)＞0,則存在δ＞0使得對所有充分大的k∈K,均有g(shù)(zk)≥δ.因φ(zk)≤φ(z0),集合{L(zk):k∈ K}包含在(分量全大于零的向量集合)的一個緊子集[6]內(nèi),所以z*∈Ω0且 L(z*)＞0.由定理 1,▽L(zk)(k ∈ K)及▽L(z*)非奇異,則{▽L(zk)-1:k∈K)}收斂到▽L(z*)-1.因0 ≤σk≤＜1,不失一般性,設(shè){σk:k∈K}收斂于σ*∈[0,1),則{dk:k∈K}收斂于滿足 ▽L(z*)d*+L(z*)=σ*β(z*)en+m的向量d*,由定理2及 α∈(0,1)得,

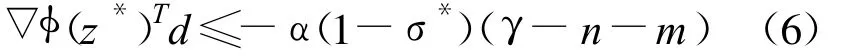
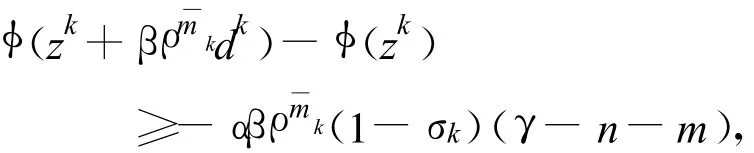
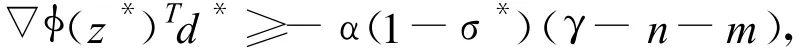
這與(6)矛盾,從而必有,

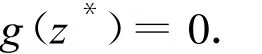
綜上,迭代點列{zk}有界且其任意聚點滿足g()=0,則對該迭代點列必有極限成立,則算法是全局收斂的.

定理3表明,g(zk)≤ε可作為算法的終止準則,其中,ε＞0是預先給定的容許誤差.

4 算 例

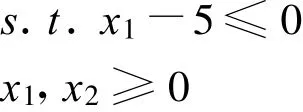
算例2

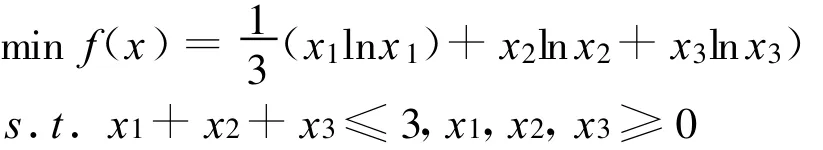
根據(jù)勢下降內(nèi)點算法,利用c#進行編程(計算機配置:CPU,AMD 2.80 GHz;RAM,3.25 GB),算法中的參數(shù)設(shè)置為,所得數(shù)值計算結(jié)果如表1所示.

表1 數(shù)值算例結(jié)果

5 結(jié) 語

本研究提出一種求解線性不等式約束凸規(guī)劃問題的勢下降內(nèi)點算法,并在一定的假設(shè)條件下,證明了該算法的全局收斂性,最后,通過數(shù)值計算驗證了該算法的有效性.

[1] Karmarkar N.A new polynomial-time algorithm for linear programming[C]//STOC'84 Proceedings of the Sixteenth annual ACM Symposium on Theory of Computing.New York:ACM Press,1984:302-311.

[2] Ye Y,Tse E.An extention of Karmarkar's projective algorithm for convex quadratic programming[J].Mathematical Programming,1989,44(1-3):157-179.

[3] Monteiro RDC,Adler I.Interior path following primal-dual algorithms[J].Mathematical Programming,1989,44(1-3):27-66.

[4] Goldfarb D,Liu S.AnPrimal interior point algorithm for convex quadratic programming[J].Mathematical Programming,1991,49(1-3):325-340.

[5] 梁昔明.求解凸二次規(guī)劃問題的勢下降內(nèi)點算法[J].高等學校計算數(shù)學學報,2002,24(1):81-86.

[6] Moteiro RDC.A Globally Convergent Primal-dual Interior Point Algorithm for convex programming[J].Mathematical Programming,1994,64(1-3):123-147.

Potential Reduction Interior-point Algorithm for Linear Convex Programming Problem with Inequality Constraints

ZHANG Tao,CHENGZhong,LVYibing
(School of Information andMathematics,Yangtze University,Jingzhou 434023,China)

In this paper,a potential reduction interior-point algorithm for the linear convex programming problem with inequality constraints is presented and the convergence of the algorithm is proved under some assumptions.Experiments with real data verify the effectiveness of the algorithm.

convex programming;inequality constraints;potential reduction interior-point algorithm

O221

A

1004-5422(2013)01-0036-03

2012-12-17.

國家自然科學基金(11201039,61273179)資助項目.

張 濤(1978—),男,博士研究生,講師,從事復雜系統(tǒng)建模與智能計算研究.