基于改進CSA－蒙哥馬利的RSA加密處理器實現

王開宇，唐禎安，趙 赟，周煜迪

（大連理工大學 電子信息與電氣工程學部，遼寧 大連 116024）

0 引 言

隨著信息化時代的不斷推進，電子商務、電子通信等諸多領域的信息安全受到越來越多的關注.為了保護電子信息，各種加密算法被應用在信息安全中.其中應用較廣泛的RSA 加密算法，是一種非對稱加密算法，即加密密鑰和解密密鑰是分開的.RSA 在FPGA 上的實現主要是利用蒙哥馬利算法將求冪取余運算轉換成硬件上容易實現的移位和相加運算，本文對算法結構做一些改進，以降低器件資源的使用，提高算法速度，最終在FPGA 上實現并進行驗證.

1 RSA 算法原理介紹

RSA 是以Rivest、Shamir、Ad－leman這3位提出者的名字而命名的.其安全性主要是依靠大數的難以分解性質.

首先，選擇兩個大素數P、Q，計算N＝P×Q，然后選擇一個非（P－1）和（Q－1）因子的公鑰E，通過（D×E）mod（P－1）（Q－1）＝1，得出私鑰D.設明文為A，密文為B，則加密過程為B＝AEmodN，相似地，解密過程為A＝BDmodN.由此可見，加密和解密運算都是求冪取余，當數很大時，如果直接計算冪再取余，無論在硬件還是軟件上實現都是不可能的.蒙哥馬利算法正是將其轉化成移位和相加并且冪和取余運算同時進行，利于在硬件上實現.

2 蒙哥馬利算法及其改進

蒙哥馬利算法的基本思想是通過移位和相加來實現模乘運算，文獻［1－2］中對蒙哥馬利算法做了些改進，改進后的算法如下：

算法1

算法2

2.1 采用CSA的蒙哥馬利算法

當位數很大時，算法2第2步中的加法運算會產生很大的延時，而采用CSA（Carry－Save－Adder）可以有效地避免長進位鏈所帶來的延時［3］.CSA 中FA 的邏輯如下：

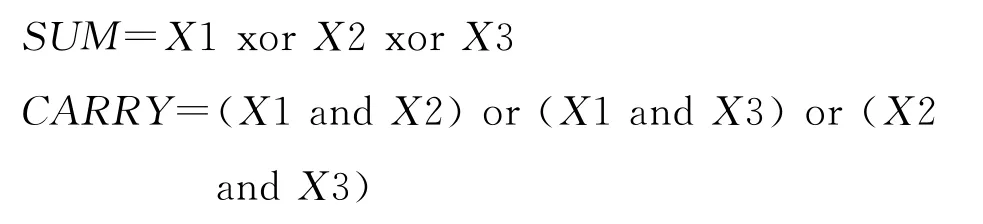
CSA 由k個FA 構成，如圖1所示.

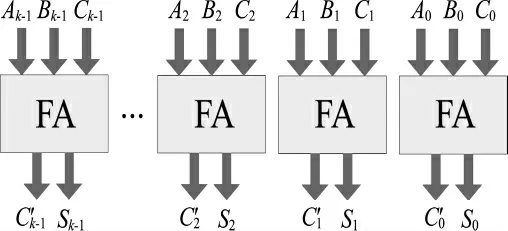
圖1 CSA 的結構Fig.1 The structure of CSA

因此采用CSA 的算法如下：

算法3

在算法3第3步中含有一個大數的加法，因此 文 獻［4］使 用 了CPA（Carry－Propagation－Adder）利用多個時鐘周期來完成最后的模乘輸出.算法結構如圖2所示.

圖2 CSA－蒙哥馬利算法結構Fig.2 The structure of CSA－Montgomery algorithm

2.2 本文對CSA－蒙哥馬利算法的改進

從CSA－蒙哥馬利算法中可以看出，每次循環中所加的數為0、B、N、B＋N中的一個，因此將其中一個CSA 的結構進行改變，即CSA＿ADD，如圖3所示，并且利用其在第一個時鐘周期計算出B＋N，通過｛SUM0，Ai｝來判斷CSA 的下一個輸入值，循環最后（SUM＋CARRY）的值可以再次利用CSA＿ADD 來計算，舍去了CPA 的使用，不但提高了速度，而且減少了資源使用.改進后的算法結構如圖4所示.

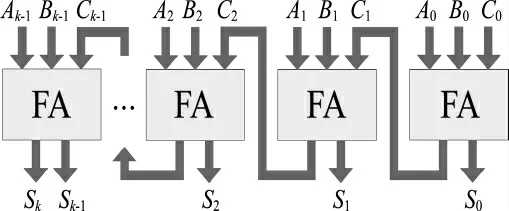
圖3 CSA＿ADD 的結構Fig.3 The structure of CSA＿ADD

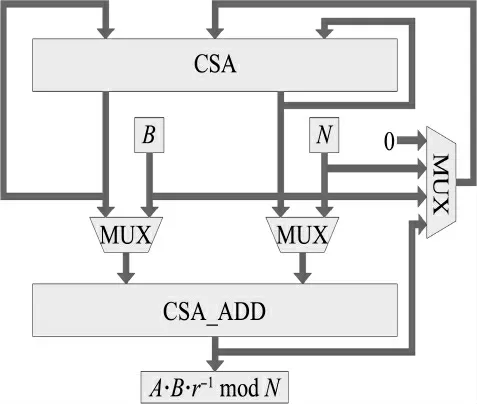
圖4 改進后的CSA－蒙哥馬利算法結構Fig.4 The structure of modified CSA－Montgomery algorithm

改進后的算法如下：

算法4

3 RSA 的算法實現

本文采用從右到左的方式掃描二進制的指數E，由于蒙哥馬利算法的返回值是A·B·2－（k＋2）modN，為了得到A·BmodN，必須先進行一步預處理Z＝M＿M（M，R，N），P＝M＿M（1，R，N），其中R是與N相關的常數，R＝22（k＋2）modN，最后再進行一次后處理P＝M＿M（1，P，N），即得到P＝MEmodN，其中M表示明文，E表示指數，N表示模數.具體步驟如下：

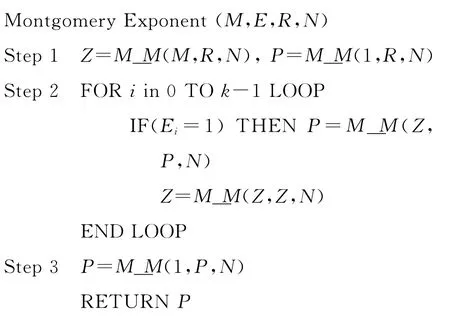
4 性能分析

本文利用Verilog 實現了密鑰位數可調的RSA 加解密處理器，利用Modelsim 仿真工具對RSA 核進行了仿真，并在XILINX 的VIRTEX5上得到了驗證.如圖5所示，當P＝MEmodN＝69mod 11＝2，與仿真結果一致.

圖5 RSA 核的仿真Fig.5 The simulation of RSA core

當加密處理器配置為1 024 位時，一次蒙哥馬利模乘運算需要1＋1 026＋1＝1 028個時鐘周期.如果指數E的0、1 出現次數相當，則一次RSA 加解密需要大約1 024＋500＋3＝1 527次模乘運算，最差情況需要1 024×2＋3＝2 051次模乘運算，則最差需要2.1×106個時鐘周期，相比文獻［5］減少了2.84%.當時鐘周期為120 MHz時，1s內可以進行約75次加解密運算.密鑰長度為1 024bits時的性能參數如表1所示.

表1 密鑰長度為1 024bits的加密處理器性能參數Tab.1 The performance of cryptoprocessor with 1 024bits key length

5 結 語

本文對采用CSA 的蒙哥馬利模乘算法結構進行了改進，省去了CPA 的使用，不但節省了器件資源，而且提高了算法速度.同時，利用Verilog編寫了可配置密鑰長度的RSA 算法的IP 核，應對不同工程的需要，可以靈活地改變密鑰長度.

［1］ Manochehri K.Modified radix－2 Montgomery modular multiplication to make it faster and simpler［C］／／Proceedings of the International Conference on Information Technology：Coding and Computing（ITCC′05）.Piscataway：IEEE Computer Society，2005：598－602.

［2］ Blum T.Montgomery modular exponentiation on reconfigurable hardware［C］／／Proceedings of 14th IEEE Symposium on Computer Arithmetic.Piscataway：IEEE Computer Society，1999：70－77.

［3］ McIvor C，McLoone M，McCaany J V.Fast Montgomery modular multiplication and RSA cryptographic processor architectures ［C］ ／／Conference Record of the Thirty.Seventh Asilomar Conference on Signals，Systems and Computers.Piscataway：IEEE，2003：379－384.

［4］ 王 旭，董 威，戎蒙恬.基于改進Montgomery模乘算法的RSA 加密處理器的實現［J］.上海交通大學學報，2004，38（2）：240－243.WANG Xu，DONG Wei，RONG Meng－tian.Implementation of RSA cryptoprocessor based on modified Montgomery modular multiplication algorithm ［J］.Journal of Shanghai Jiaotong University，2004，38（2）：240－243.

［5］ Kwon Tack－won，You Chang－seck，Heo Won－seok，etal.Two implementation methods of a 1024－bit RSA cryptoprocessor based on modified Montgomery algorithm ［C］／／IEEE International Symposium on Circuits and Systems－ISCAS.Piscataway：IEEE，2001：650－653.