2－qubit系統的糾纏魯棒性

史淑惠，許龍飛

（1.邯鄲學院 物理與電氣工程系，河北 邯鄲 056005；2.河北大學 物理科學與技術學院，河北 保定 071002）

量子糾纏是一個最微妙和迷人的自然現象，在量子計算和量子信息中起著非常重要的作用［1］.量子糾纏作為量子信息過程的重要資源，可以應用到許多方面如：量子隱形傳態［2］、量子計算［3］、量子編碼［4］、量子密碼［5］等等.然而，對于一個量子系統而言，它必然在處于某種環境中并與環境發生相互作用，通常會導致系統糾纏的降低.在量子信息處理上，這種退相干使得系統出現不穩定的現象.因此，研究量子糾纏的動力學特性尤為重要.最近有許多相關的工作被報道，例如，一個處于糾纏的量子態在環境的影響下其糾纏度會在有限的時間內變為零，這種現象被稱為糾纏猝死（entanglement sudden death，ESD）［6］，并且這一現象已經在2－quibt光學系統中被觀測到［7］.量子糾纏在環境噪聲的影響下是非常脆弱易被破壞的，因此糾纏態對噪聲的抵抗能力在量子信息過程中是一個很重要的問題.糾纏的魯棒性便是反映該能力的一個量.1999年，Vidal和Tarrach［8］將一個糾纏態與可分離態混合時當糾纏恰好消失時可分離態混入的比例稱為該態的魯棒性.2002年，Simon和Kempe［9］考慮了將處于糾纏態的qubit置于相互獨立的環境中的情況，以完全退糾纏時噪聲的大小作為糾纏態的魯棒性.2010年，Zhao和Deng［10］給出了2－qubit純態在退極化噪聲下魯棒性與糾纏度的簡單關系.本文基于量子糾纏這一熱門領域，通過分析在退極化噪聲下糾纏態隨時間的演化特性，并給出一類2－qubit態的糾纏抗噪聲能力——糾纏魯棒性解析關系.

1 模型

對于開放系統而言，退相干是一種常見的量子現象.在研究的問題中，考慮一個初始時刻具有糾纏的2－qubit系統在退極化噪聲下的演化特性，此外單qubit能夠與環境獨立地發生相互作用.假設所有qubit受到相同的退極化過程，通過主方程的方法可以得到單qubit的動力學演化形式.系統與環境發生相互作用，在海森堡繪景下，系統的演化過程可以用Liouville方程表示出來，利用量子力學中的Born近似，將系統的演化內核部分保留到二階項.同時忽略環境的記憶效應（取Markovian近似），于是得到Lindblad形式的主方程.將其表示為Kraus算符的形式［11］

2 糾纏度

3 2－qubit糾纏猝死現象

在退極化噪聲下，為了不失一般性，從兩方面考慮2－qubit系統：純態和混態.

對于純態而言，它是最簡單的兩體系統.一般的2－qubit純態可以表示為｜ψ〉＝a｜00〉＋b｜01〉＋c｜10〉＋d｜11〉（其中｜a｜2＋｜b｜2＋｜c｜2＋｜d｜2＝1），在局域幺正操作下，任意2－qubit純態等價于｜ψ〉＝cosθ｜00〉＋sinθ｜11〉（θ∈［0，π／2］），這是純態的Schmidt分解形式［1］.在退極化噪聲的作用下，2－qubit純態的糾纏 Concurrence變為

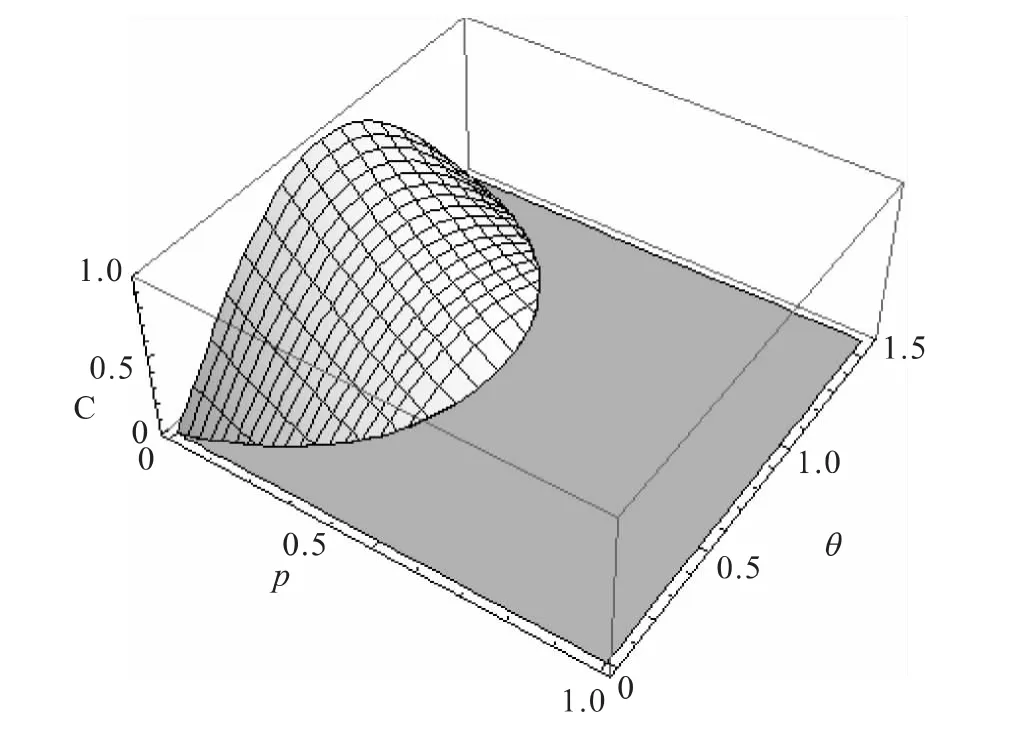
圖1 純態的糾纏隨參數的演化Fig.1 Plot of the evolution of Concurrence with parameters for pure state

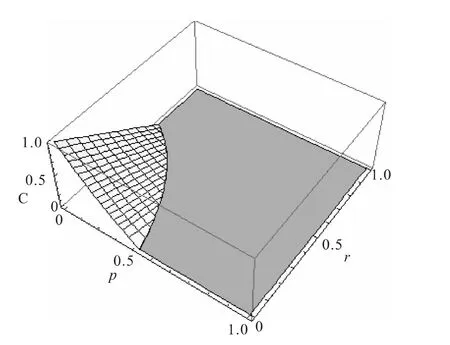
圖2 Werner態的糾纏隨參數演化Fig.2 Plot of the evolution of Concurrence with parameters for Werner state

因此不難看出，在2－qubit系統中，無論是純態還是混態都出現了糾纏猝死現象，但是這2種態的糾纏猝死特性并不一致.對于純態系統而言，系統本身比較簡單，在退極化噪聲下呈線性改變；而在混態系統中狀態參量逐漸增多，在噪聲作用下多參數混態系統的演化狀態往往不再是單調的變化，狀態將變得更加復雜.

下面介紹一個物理量——糾纏魯棒性，用它來分析解決在相同環境下，量子系統對噪聲的抵抗能力將會如何，并且以此來區分該能力的強弱.

4 糾纏魯棒性

首先，不同于文獻［8－10］中對糾纏魯棒性的定義，定義糾纏魯棒性為［16］

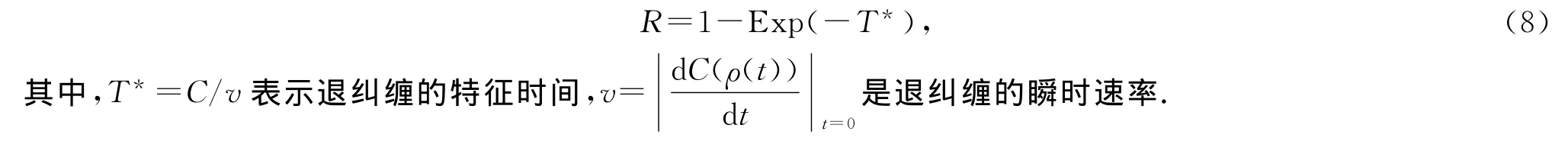
在退極化噪聲下，用數值模擬的方法給出了糾纏和糾纏魯棒性的關系（如圖3）.從圖3中，明顯可以看到糾纏魯棒性存在邊界，那么邊界態對應形式是什么呢？

因為2－qubit純態是2－qubit態中最簡單的狀態，故首先考慮這一形式.對于任意2－qubit純態｜ψ〉＝cosθ｜00〉＋sinθ｜11〉（θ∈［0，π／2］），利用p＝1－exp［－κt］（由于κ表示衰減常數且在相同環境下比較系統穩定性方面是一致的，因此可取κ＝1），可以得到退糾纏速率

結果與文獻［10］很相似，其糾纏魯棒性僅僅取決于糾纏度C.另外，可以看到純態的糾纏和魯棒性的關系正好對應圖3中的邊界，圖中用黑粗實線標出.

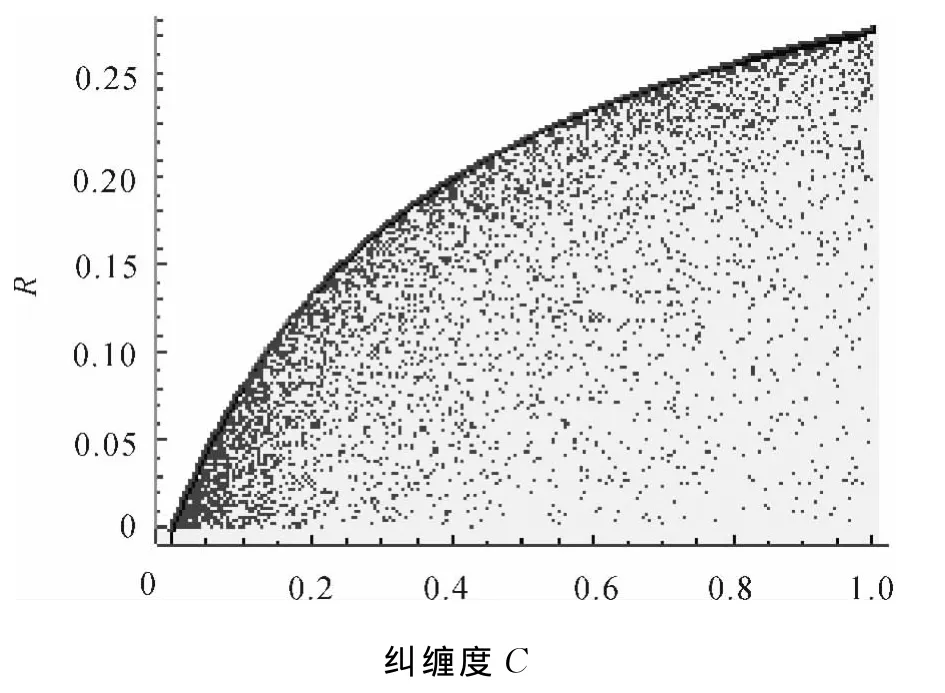
圖3 10 000個任意2－qubit態的糾纏魯棒性R與糾纏（Concurrence）的關系Fig.3 Plots of the relations between the entanglement robustness and Concurrence of randomly generated two－qubit states 10 000randomly generated states and the curve showing the upper bound

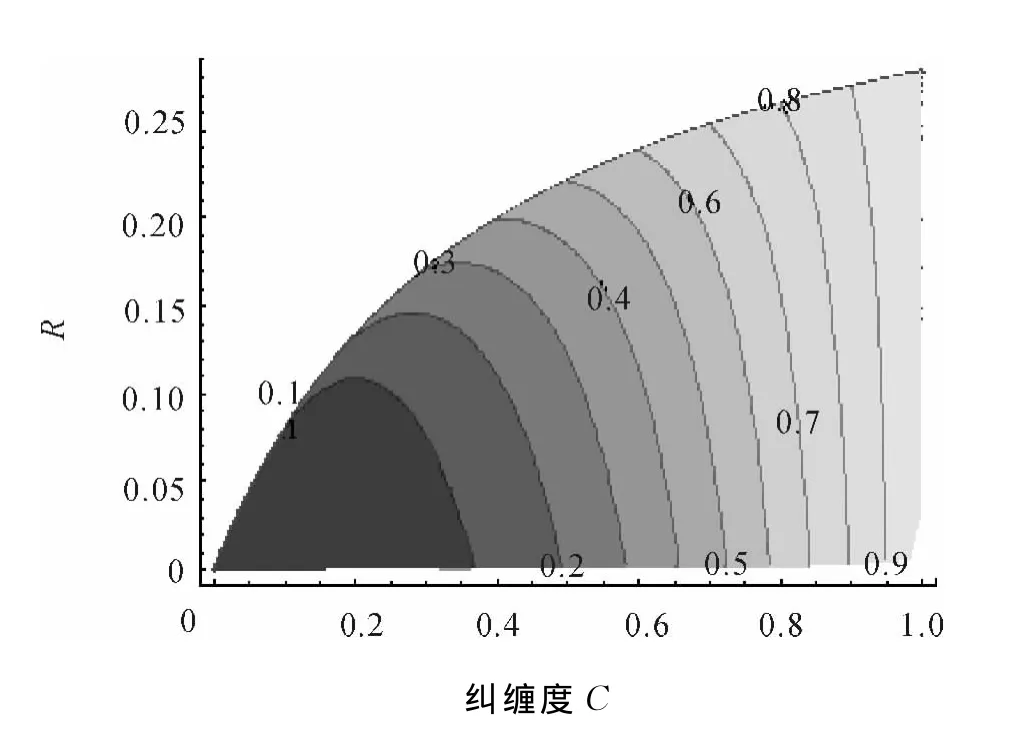
圖4 Negativity對糾纏魯棒性R的影響（等高線表示Negativity的值）Fig.4 Plot of the effect of Negativity on the entanglement robustness，with the contours of the Negativity

為了進一步分析問題，考慮一類態ansatz態［17］

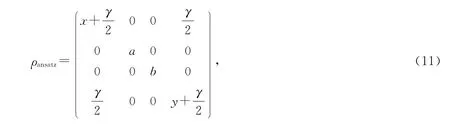
其中0≤x，y，a，b，γ≤1且x＋y＋a＋b＋γ＝1，可以看到 Werner態也滿足ansatz態的形式.該態的糾纏度Concurrence為

對于這類態而言，發現在退極化噪聲作用下態的形式不發生改變，只是參數會相應改變.在退極化噪聲作用下，可以看到所研究的態ρansatz變為ρ（t），即

從式（16）可以看到ansatz態的糾纏魯棒性僅僅取決于3個參量γ，a，b，即一旦這3個參量給定，那么糾纏魯棒性就被確定下來了.

當a＝b且a，b≠1時，該態的魯棒性為R＝1－Exp［－C／（2C＋1）］，這與純態的結果一致，滿足任意2－qubit態的上邊界關系（見圖3）.另外，還可以看到，在退極化噪聲作用下，當初態為純態時，系統演化過程中糾纏魯棒性始終保持R－C（其中R＝1－Exp［－C／（2C＋1）］）這一關系.如果初態為Bell態（即最大糾纏態C＝1），那么該態在退極化噪聲下逐步演化將會沿著邊界線（圖3中的實線）進行變化，從最大糾纏態逐漸變為無糾纏態；糾纏魯棒性也會相應減小甚至變成0，即抗噪聲能力逐漸降低.對于其他滿足a＝b糾纏態（可看出Werner態只是屬于這類態中的一種形式）的演化情況同純態的情況相似，只是起始糾纏大小不同而已.對于一般ansatz態（a≠b且a，b不同時為0）來說，也有相似結論，只是演化曲線Ra－Ca不再是邊界線.

通過以上分析，可以看到對于該類對角混態（ansatz態），在每一時刻糾纏的魯棒性（即抗噪聲能力）都可以被確定，即任意時刻ansatz態的糾纏魯棒性都是確定的.另外，根據糾纏和魯棒性的關系，可看出糾纏猝死時間在很大程度上取決于初始糾纏大小和糾纏魯棒性，而且糾纏魯棒性越大糾纏猝死時間越長.

下面分析其他糾纏度量對糾纏魯棒性的影響，如Negativity［18］.任意2－qubit糾纏可以表示為N＝的負本征值，T表示對ρ的子系統A的部分轉置.對于ansatz態來說，為AAB了方便，取x＝y＝0，此時態記為ρn.為了更加清晰地呈現問題，將Negativity作為等高線來刻畫另一糾纏度對糾纏魯棒性的影響（如圖4）.從圖4中，可以看到，當Concurrence一定時，Negativity越大糾纏魯棒性越強，那么糾纏猝死的時間將會更長.由于2－qubit系統的糾纏的度量方式是多樣化的，所以對于其他糾纏度的影響在此就不再一一贅述.

5 結論

分析了2－qubit量子系統在退極化噪聲作用下的一些糾纏特性.通過分析對角混態的糾纏魯棒性（系統抵抗噪聲的能力），給出了這類量子態的解析關系.由于兩比特系統在具有各向同性噪聲（退極化噪聲）下，對角混態（ansatz）可以通過不改變本身糾纏的局域幺正操作得到絕大多數的兩比特態，因此說系統糾纏猝死時間對糾纏和糾纏魯棒性有一定的依賴性.糾纏作為量子通訊和量子計算的信息載體，其穩定性是至關重要的，選擇具有較強抗噪能力的量子態是很必要的，期望對系統糾纏魯棒性的分析可以為量子態調控方面起到一定的促進作用.

［1］NIELSEN M A，CHUANG I L.量子計算和量子信息［M］.鄭大鐘，趙千川，譯.北京：清華大學出版社，2005.

［2］BENNETT C，BRASSARD G，CREPEAU C，et al.Teleporting an unknown quantum state via dual classical and Ein

stein－Podolsky－Rosen channels［J］.Phys Rev Lett，1993，70：1895－1899.

［3］GROVER L K.Quantum mechanics helps in searching for a needle in a haystack［J］.Phys Rev Lett，1997，79：325－328.［4］BENNETT C H，WIESNER S J.Communication via one－and two－particle operators on Einstein －Podolsky －Rosen states［J］.Phys Rev Lett，1992，69：2881－2884.

［5］EKERT A K.Quantum cryptography based on Bell's theorem ［J］.Phys Rev Lett，1991，67：661－663.

［6］YU T，EBERLY J H.Finite－time disentanglement via spontaneous emission［J］.Phys Rev Lett，2004，93：140404.［7］ALMEIDA M P，MELO F D，HOR－MEYLL M，et al.Environment－induced sudden death of entanglement［J］.Science，2007，316，579－582.

［8］VIDAL G，TARRACH R.Robustness of entanglement［J］.Phys Rev A，1999，59：141－155.

［9］SIMON C，KEMPE J.Robustness of multiparty entanglement［J］.Phys Rev A，2002 65：052327（1－4）.

［10］ZHAO Baokui，DENG Fuguo.Residual effect on the robustness of multiqubit entanglement［J］.Phys Rev A，2010，82：014301（1－4）.

［11］BORRAS A，MAJTEY A，PLASTINO A，et al.Robustness of highly entangled multiqubit states under decoherence［J］.Phys Rev A，2009，79：022108.

［12］DüR W，BRIEGEL H.Stability of macroscopic entanglement under decoherence［J］.Physical review letters，2004，92：180403.

［13］HILL S，WOOTTERS W.Entanglement of a pair of quantum bits［J］.Phys Rev Lett，1997，78：5022－5025.

［14］WOOTTERS W.Entanglement of formation of an arbitrary state of two qubits［J］.Phys Rev Lett，1998，80：2245－2248.

［15］WERNER R F.Quantum states with Einstein－Podolsky－Rosen correlations admitting a hidden－variable model［J］.Phys Rev A，1989，40：4277－4281.

［16］ZHANG Fulin，JIANG Yue，LIANG Mailin，et al.Speed of disentanglement in multiqubit systems under depolarizing channel［J］.Annals of Physics，2013，333：136－154.

［17］MUNRO W，JAMES D F V，WHITE A G，et al.Maximizing the entanglement of two mixed qubits［J］.Phys Rev A，2001，64：030302（R）.

［18］YCZKOWSKI K，HORODECKI P，SANPERA A，et al.Volume of the set of separable states［J］.Phys Rev A，1998，58：883－892.