基于LMIs的連續Markovian跳變系統穩定性分析及控制器設計

王瑾，董澤

（華北電力大學控制科學與計算機學院，河北保定071002）

隨著工業科技的不斷發展，人們對工程系統性能的要求愈加嚴格.然而工業環境的不斷變化、子系統之間愈加復雜的聯結方式、工作范圍的不同與零件故障等變化，導致系統結構和參數均發生了跳躍性變化.因此人們不得不采用一種特殊的隨機系統——Markovian跳躍系統，準確地描述出系統結構隨著時間變化的規律，從而使系統的性能不受上述各種因素的影響.Markovian跳躍系統的構成可以分為2部分：系統的模式與系統的狀態［1］.根據系統概率分布，在馬爾可夫鏈的每個部分都可以從一個狀態轉換到另一個狀態，或者保持在當前狀態.與不同狀態改變相關的概率稱為過渡概率，狀態的更改稱為過渡［2］.

連續Markovian跳躍系統的奠基性研究始于Krasovskii和Lidskii的工作，隨著該類系統隨機鎮定性問題的解決，Markovian跳躍系統的理論研究拉開了帷幕.連續Markovian跳躍系統的數學表達式在文獻［3］中給出如下：

這里，系統模式間切換由r（t）決定，且r（t）是在有限集合F＝｛1，…，N｝內取值的馬爾科夫過程.其狀態轉移概率矩陣為

Markovian跳躍系統因為可以描述許多實際的系統而受到廣泛關注.據相關文獻資料顯示，該研究的成果已經在核電廠控制系統、無線伺服控制系統、電力系統、飛行器控制系統、通訊系統和制造系統等工程領域得到應用［4］.

1 LMIs理論基礎

1.1 LMIs的基本形式

由文獻［3］可知，LMIs（線性矩陣不等式）通常具有如下的形式：

式（1）中，x∈Rm為需要求解的變量，并且矩陣，i＝0.1，…，m為對稱的而且已知.由上式可以得到F（x）為正定矩陣，換句話說就是對于非零數u∈Rn，存在不等式uTF（x）u＞0，所以，上式實際上是n個有關x的不等式，因此，F（x）的主子式均需大于零.并且需要指出，式中所得解集是凸的.

由不等式的一般結構形式可以知道，不等式的構成即是不等式的最基本的問題，其他所存在的任何問題都是在這個基本形式上添加與修改的，控制器的設計同樣是根據不等式從而得到的參數.

1.2 線性矩陣不等式的方法

［3］中有2個引理，可以將非線性矩陣不等式條件轉化為線性矩陣不等式條件，如下所示.1）Schur補引理

其中Q，QT，R＝RT，S為適當維度的矩陣.

2）范數有界矩陣消除法

給定對稱矩陣Q，適當維度矩陣D，E和F（t），若

對所有滿足FT（t）F（t）≤I的矩陣F（t）成立，當且僅當存在1個標量ε＞0，使得

2 Markovian跳躍系統的穩定性條件及分析

2.1 問題描述

對于馬爾科夫系統的一個給定的概率空間（ΩFP），其中Ω是采樣空間，F是采樣空間的σ‐算子，P是F上的概率測度.由文獻［4］可知，在這個空間中，設定連續的馬爾科夫跳躍系統對象為

其中x（t）∈Rn是狀態向量，r（t）＝i，表示系統在t時刻所在的位置狀態，取值在集合L＝（1，2，…，N）中.

馬爾科夫跳變系統中，表示系統跳變過程的量：轉移概率矩陣為

2.2 穩定性分析

2.2.1 Lyapunov穩定法

馬爾科夫跳躍系統穩定性判斷采用李雅普諾夫穩定法，由文獻［5］可以知道，穩定性的實質問題是考察系統由初始狀態擾動所引起的受擾運動是否可以趨近或者返回到原平衡狀態.

系統＝f［x，t］，平衡狀態是Xe＝0，此時滿足f（xe）＝0.如果有一個標量函數V（x），滿足V（x）對所有x都有連續一階偏導數，同時也滿足V（x）正定，則

1）如果V（x）沿狀態軌跡的方向計算時間導數（x）＝dV（x）／dt是半負定的，則平衡狀態是穩定的；

2）如果（x）是負定的，或雖然（x）是半負定的，但是對任何初始狀態不恒是零，則平衡狀態是漸進穩定的.當‖x‖→∞的時候，V（x）→∞，系統是大范圍漸進穩定的；

3）如果（x）是正定的，則平衡狀態下不穩定.

V（x）通常選成二次型，判斷二次型V（x）＝的正定性可以用Sylvester準則去確定，也就是正定的充要條件是P的所有主子行列式都是正的；如果P的所有主子行列式都是非負，是正半定；若－V（x）是正定，則V（x）就是負定；若－V（x）是正半定，則V（x）就是負半定.

李氏穩定第2法是去設定一個能量方程，去驗證馬爾科夫過程的能量為逐漸衰減的，就可以找到系統穩定的條件.

2.2.2 穩定性證明

定理1 由文獻［6］可知，已知系統（3），若存在正定矩陣P，滿足下列LMIs：

那么系統是穩定的.

設定能量方程為

其中矩陣P為正定矩陣，若要求穩定，則要求能量方程是逐漸衰減的［7］，即＜0，

其中￡是隨機過程的弱微分算子.

將對象代入（t）＝A（trt）x（t），得到

要使式（6）＜0，可知其為二次型形式，可寫成矩陣形式

式（7）為系統的LMI形式，由此可知，使￡V1＜0，即

由式（8）可知，在此條件下，能量方程是逐漸衰減的，因此，式（8）即為馬爾科夫跳變系統的穩定條件.

3 Markovian跳躍系統的控制器設計

Markovian跳躍系統是一個隨機性較強的系統，在控制系統的應用中，為了防止發生數據丟失、錯發，要設計控制器使系統穩定.

3.1 問題描述

對于給定的概率空間（Ω，F，P），其中Ω是采樣空間，F是采樣空間的σ－算子，且P是F上的概率測度.在此概率空間中，考慮如下的連續時滯Markovian跳變系統［10］：

其中x（t）∈Rn是狀態向量，u（t）∈RP是控制輸入，｛rt｝是右連續的且在有限集合L＝｛1，2，…，N｝取值的連續時間.

根據系統的性質，采用如下的模式依賴狀態反饋控制器：

其中，Ki，i∈L是待求的模式依賴狀態反饋控制增益.

將（10）式代入到馬爾科夫跳變系統（9）中，得到如

的閉環系統.

3.2 Markovian跳變系統穩定性控制原理

設計控制器的前提就是保證系統的穩定性，因此，設計原理就是在馬爾科夫跳變系統穩定條件下得到控制器.由文獻［11－12］可知以下定理及引理.

定理2

Ⅰ.對于系統（9），當u（t）＝0時，稱連續時間廣義Markov系統是正則的，若

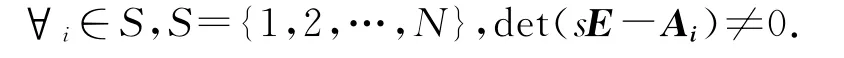
Ⅱ.當u（t）＝0時，稱連續時間廣義Markov跳變系統是無脈沖的，若?i∈S，

Ⅲ.當u（t）＝0時，稱連續時間廣義Markov跳變系統是隨機穩定的，若對于任意初始狀態x0∈Rn和r0∈S，存在標量M（x0，r0）＞0，使下式成立：

其中E表示數學期望.

引理1 系統（9）是隨機穩定的充要條件為：存在矩陣，使得下列LMIs成立

3.3 Markovian跳變系統控制器設計

由系統的穩定條件，根據李雅普諾夫穩定條件，設能量方程為［13］

其中矩陣P為正定矩陣，若要求穩定，則要求能量方程是逐漸衰減的，即

其中是隨機過程的弱微分算子.

對能量方程弱微分，得

將系統對象（t）＝A（t，rt）x（t）＋B（t，rt）Kix（t）代入，得到

將上式化為二次型

由二次型可知，要想滿足系統穩定的充要條件，要使二次型為小于零的，即式（15）

由式（15）可知，（15）即為系統的穩定條件，由此條件，可以得到Ki（t），得到控制器對象.可知（15）為Lyapunov矩陣形式，以Ai，Bi，Pi，Ki代替各矩陣變量，將其寫為

以分別左乘和右乘（16），得到

由此可知，可利用Schur補引理，得到下列矩陣不等式：

其中，＊代表矩陣的對陣部分.令，得到

其中，令Yi＝KiXi，得到

由以上矩陣不等式可知，要想得到控制器表達式，要利用LMIs解得（19）關于Xi，Yi的解，其中，控制器的表達形式為

使用Matlab進行求解，可編寫程序得到結果.

3.4 數值算例

經過Matlab仿真得到

因為，可得到K1＝［1.002 1.448］；K2＝［0.832 1 2.089 5］，Result：best value of t：－0.796 547，t的值在負半平面，說明系統控制穩定，所以設計的控制器可以實現對系統的控制.

4 結束語

本文針對連續Markovian跳變系統的穩定性進行了研究，通過Lyapunov定理得到了穩定性條件，在對系統增加了隨機環節后，基于Lyapunov定理，利用LMIs方法設計實現了控制器，通過數值算例仿真驗證，對于隨機性較強的Markovian跳變系統，該控制器可以實現較好的控制穩定效果，可以有效應用于實際系統的控制.

參 考 文 獻：

［1] FENG Xiangbo，LAPARO K A，JI Yuandong，et al.Stability Properties of Jump Linear System［J］.IEEE Trans Automat Control，1992，37（1）：38－53.

［2] DANIEL W S.Markov過程導論［M］.北京：高等教育出版社，2007：12.

［3] 俞力.魯棒控制－線性矩陣不等式處理方法［M］.北京：清華大學出版社，2002.

［4] 姚秀明.混雜Markovian跳躍系統的分析與綜合［M］.哈爾濱：哈爾濱工業大學，2010.

［5] 謝克明.現代控制理論基礎［M］.北京：北京工業大學出版社，2008.

［6] JI Yuandong，CHIZECK H J.Controllability，stabilizability，and continuous－time Markovian jump linear quadratic control［J］.IEEE Trans Automat Control，1990，35（7）：777－788.

［7] MOROZAN T.Stability and control for linear systems with jump Markov peturbations［J］.Stochastic Analytic Application，1996，23：1015－1022.

［8] COSTA O L V，GEROMEL J C.Continuous－time state－feedback，H2－control of Markovian jump linear system via convex analysis［J］.Automatica，1999，35（2）；259－268.

［9] KRASOVSKII N N，LIDSKII E A.Analytic design of controller in systems with random attributes［J］.Automatic Remote Contr 1961，27：Part1，1021－1025，Part2，1141－1146.

［10] XU Shengyuan，LAM J.Improved delay－dependent stability criteria for time－delay systems［J］.IEEE Trans Automatic Control，2005，50（3）：384－387.

［11] 孫超.不確定離散時滯系統的魯棒控制［M］.哈爾濱：哈爾濱理工大學，2003.

［12] HE Yong，WANG Qingguo，XIE Lihua，et al.Further improvement of free－weighting matrices technique for systems with time－varying delay［J］.IEEE Trans Automatic Control，2007，52（2）：293－299.

［13] WU Min，HE Yong，SHE Jinhua，et al.Delay－dependent criteria for robust stability of time－varying delay systems［J］.Automatica，2004（3）：1435－1439.