基于FLUENT的某型空空導彈空氣動力分析

王 洋，佟惠軍，楊 林

(空軍航空大學軍械工程系，長春 130022)

空空導彈空氣動力參數是評定空空導彈作戰和運用的必不可少的技術依據。通常在對導彈空氣動力參數進行求解時都沒有考慮舵面偏轉角度對整個導彈飛行過程的空氣動力的影響，使得計算精度在一定程度上有所不足，因此考慮使用FLUENT軟件包對其進行研究。利用FLUENT軟件進行數值模擬，具備花費少，又可以給出流場內細節的定量描述，能在較廣泛的流動參數范圍內給出流場的定量結果，并且不受試驗中固有約束因素的影響。通常應用FLUENT軟件包進行計算主要分為以下幾個步驟:網格劃分、選擇正選取適當的計算模型、確立所需邊界條件與計算格式。其中主要部分為網格的劃分與計算模型的選取。

1 網格劃分

劃分網格大致上有兩種主要方法，一個是結構性網格，另一個是非結構性網格。結構性網格是指網格區域內所有內部點都具有相同的毗鄰單元。非結構性網格則與之相反，即與網格剖分區域內的不同內點相連的網格數目不同。

解算像空空導彈這種具有復雜幾何結構的空氣動力系數的問題，一種有效的方法是采用非結構化網格。由于非結構網格可以采用任意形狀的單元格，單元邊的數目也無限制，使其能夠很好地模擬自然幾何邊界。同時非結構網格生成簡單，并且還具有比較好的可調節性和可控性，生成網格如圖1所示。

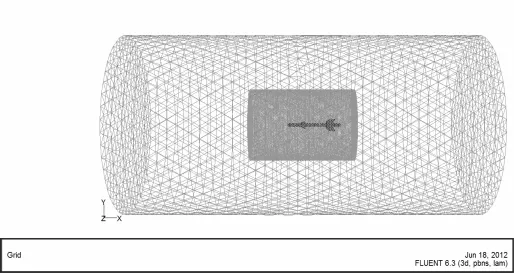
圖1 彈體及流場網格

2 湍流模型的選擇

FLUENT中可選擇的湍流模型主要包括:單方程(Spalart-Allmaras)模型、雙方程模型(標準k－ε模型、重整化群k－ε模型、可實現(Realizable)k－ε模型)及雷諾應力模型和大渦模擬。

對于飛行器等繞流流場的分析，在進行求解時多選擇Spalart-Allmaras湍流模型，此模型是一個比較簡單的單方程模型，只求解一個關于渦粘性的輸運方程，計算量較小。

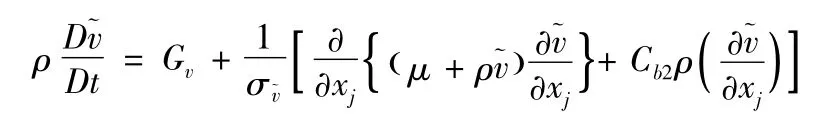
其中，Gν是湍流粘性產生項;Yν是由壁面阻擋和粘性阻尼引起的湍流粘性的減少;σ?ν和Cb2是常數;ν是分子運動粘性系數。

湍流粘性系數用如下公式計算:

由于平均應變率對湍流產生也起到很大作用，FLUENT在處理過程中，定義S為:

在渦量超過應變率的計算區域計算出來的渦旋粘性系數變小。這適合渦流靠近渦旋中心的區域，那里只有“單純”的旋轉，湍流受到抑止。包含應變張量的影響更能體現旋轉對湍流的影響。忽略了平均應變，估計的渦旋粘性系數產生項偏高。

湍流粘性系數減少項Yν:

3 邊界條件與計算格式

計算時采用壓強遠場條件，這種邊界條件通常用于給定可壓縮流的自由流邊界條件，在給定流體的馬赫數和確定其他參數條件后，給定無限遠處的壓強條件。壓強遠場條件通常應用于可壓縮流計算，主要設置項目為來流的馬赫數和靜參數條件。

使用壓強遠場邊界條件需要氣體密度用理想氣體假設進行計算，為了模擬“無限遠”要求，計算邊界需要距離物體有足夠遠的距離，通常要求其邊界距離模型約20倍弦長。對于計算格式的選擇FLUENT軟件包中主要有一階迎風格式和二階迎風格式兩種方式。

兩種計算格式都可以理解為流場變量在上游網格單元控制點展開的特例，一階迎風格式僅保留Taylor級數的第一項，認為本地單元邊界點的值與上游網格單元控制點上的值相等，其格式精度為一階精度。二階迎風格式在保留了Taylor級數的第一項同時還保留了第二項，認為本地邊界點的值等于上游網格控制點的值與一個增量的和，因而其精度為二階精度。

一階迎風格式在解決結構網格問題時，其計算速度要明顯快于二階迎風格式，并且有良好的穩定性。而對于非結構網格問題，由于流動方向與網格并不一定相一致，因此采用一階迎風格式則會長生很大的誤差，此時應該選用二階格式。

4 計算結果與分析

通過對FLUENT測出的各項數據進行擬合可以得出當攻角為0°，馬赫數為1.2時導彈的升力及阻力系數隨舵偏角變化的規律如圖2所示。

從圖2中可以看出在攻角為0°的情況下，舵偏角變化對升力系數的影響近似表現為線性關系，而且由于導彈彈體結構對稱的原因，在舵偏角為±20°和±10°時，其阻力系數近似相等，表現出明顯的對稱性。攻角為3°，馬赫數為1.2時導彈的升力及阻力系數隨舵偏角變化的規律如圖3所示。

從圖3中可以明顯看出當攻角不再為0°時，舵偏角的變化改變了流過導彈氣流的對稱性，升力系數曲線線性度開始變差，尤其是在舵偏角轉到20°極限值附近，其變化率明顯減慢，其升力系數近似為常值。對于阻力系數，其對稱中心明顯發生偏移。

攻角為6°，馬赫數為1.2時導彈的升力及阻力系數隨舵偏角變化的規律如圖4所示。

圖2 0°攻角時的氣動系數

圖3 3°攻角時的氣動系數

圖4 6°攻角時的氣動系數

通過與圖2和圖3的對比，從圖4中可以發現當攻角繼續增大時，舵偏角在一定范圍內其對升力系數的改變作用將不太明顯，超出這個范圍時則繼續表現為一定的線性關系。對于阻力系數，其增長幅度將逐漸減小。

5 結束語

實驗結果表明，舵偏角的變化對整個導彈空氣動力參數的改變有著極為重要的作用，在對導彈外彈道進行解算的過程中將是一個不可忽視的因素，這對于提高導彈的作戰效果有著不可忽視的影響。同時FLUENT軟件包很好的對整個導彈的空氣動力參數進行了解算，充分地體現了其易操作并且節省時間與經費的特點。

［1］ 于勇.fluent進階與入門教程［M］.北京:北京理工大學出版社，2008.

［2］ 張楓.竇磊.基于fluent軟件包的制導炮彈氣動力參數計算技術研究［D］.南京:南京理工大學，2010.

［3］ 林曉宏.N－S方程并行算法研究及在彈箭流場中的應用［D］.南京:南京理工大學，2009.

［4］ 錢杏芳，林瑞雄，趙亞男.導彈飛行力學［M］.北京:北京理工大學出版社，2000.

［5］ 李浩，趙忠良，范召林.風洞虛擬飛行試驗模擬方法研究［J］.實驗流體力學，2011，25(6):72 －76.

［6］ 朱自強.應用計算流體力學［M］.第2版.北京:北京航空航天大學出版社，1998.

［7］ 趙洪章，岳春國，李進賢.基于Fluent的導彈氣動特性計算［J］.彈箭與制導學報，2007(2):203－207.

［8］ 肖志祥，李鳳蔚，鄂秦.湍流模型在復雜流場數值模擬中的應用［J］.計算物理，2003(4):335－345.

［9］ 齊玉文.高超聲速彈箭尾翼(彈翼)的氣動力與氣動熱研究［M］.南京:南京理工大學，2008.

［10］何開鋒，王文正，錢煒祺.根據風洞試驗結果建立有尾翼導彈數學模型［J］.流體力學實驗與測量，2004，18(4):62－66.

［11］謝昊.并行計算在CFD問題中的應用［D］.成都:四川大學，2005.

［12］史金光，王中原，曹小兵，等.一維彈道修正彈氣動力計算方法和射程修正量分析［J］.火力與指揮控制，2010(7):80－83.

(責任編輯周江川)