基于符號(hào)分析的極大聯(lián)合熵延遲時(shí)間求取方法*

張淑清 李新新 張立國 胡永濤 李亮

(燕山大學(xué)電氣工程學(xué)院，河北省測試計(jì)量技術(shù)及儀器重點(diǎn)實(shí)驗(yàn)室，秦皇島 066004)

(2012年11月30日收到;2013年2月4日收到修改稿)

1 引言

混沌自從被確認(rèn)是長期可控制的和短期可預(yù)測以后，其研究課題引起了大家廣泛的興趣.然而相空間重構(gòu)作為混沌時(shí)間序列處理中的重要課題，其最佳延遲時(shí)間的選取至關(guān)重要.對于時(shí)間序列X(n)，過小的延遲時(shí)間τ將導(dǎo)致信息的冗余，使得重構(gòu)的坐標(biāo)之間不可分辨，過大的τ將使延遲坐標(biāo)之間毫不相關(guān)，不能代表真實(shí)的動(dòng)力系統(tǒng)[1]，因此選取最佳延遲時(shí)間需要使X(n)和X(n+τ)最大限度相互獨(dú)立卻又不是完全無關(guān).

確定相空間重構(gòu)最佳延遲時(shí)間的方法有互信息函數(shù)法、自相關(guān)函數(shù)法和平均位移法等.其中互信息函數(shù)方法是估計(jì)重構(gòu)相空間延遲時(shí)間的一種有效方法，它在相空間重構(gòu)中有很廣泛的應(yīng)用.Shaw首先提出互信息第一次達(dá)到最小時(shí)滯時(shí)作為相空間重構(gòu)的最佳延遲時(shí)間[2]，F(xiàn)aster給出了互信息計(jì)算的遞歸算法.但其提出的劃分網(wǎng)格計(jì)算方法過于復(fù)雜，不易于編程實(shí)現(xiàn)及推廣使用.國內(nèi)學(xué)者提出了相應(yīng)的改進(jìn)算法并獲得很好的應(yīng)用，這在一定程度上激發(fā)了人們對準(zhǔn)確快速地選取相空間重構(gòu)中最佳延遲時(shí)間的興趣[3].文獻(xiàn)[4]提出了確定延遲時(shí)間變量的聯(lián)合熵之第一極大準(zhǔn)則，相對互信息方法減少了計(jì)算量，但在求取聯(lián)合熵時(shí)采用劃分網(wǎng)格的方法，計(jì)算相對復(fù)雜而且誤差較大;文獻(xiàn)[5，6]提出了改進(jìn)的網(wǎng)格標(biāo)記法，該方法與符號(hào)分析法相比計(jì)算仍然相對復(fù)雜;文獻(xiàn)[7]提出的符號(hào)分析法求取互信函數(shù)，從而確定出最佳延遲時(shí)間，可避免復(fù)雜的網(wǎng)格劃分和標(biāo)記，但需同時(shí)求取X(n)和X(n+τ)的各自信息熵及其聯(lián)合熵.本文提出了基于符號(hào)分析的極大聯(lián)合熵延遲時(shí)間求取方法，較好地解決了上述方法中所存在的各種問題，可以快速有效地提取混沌動(dòng)力系統(tǒng)中有用定量信息，重構(gòu)系統(tǒng)的相空間.

2 最佳延遲時(shí)間的極大聯(lián)合熵準(zhǔn)則

考慮時(shí)間序列X(n)及其延遲時(shí)間序列Xτ(n)=X(n+τ)，n=1,2,···,N.根據(jù)互信息函數(shù)的遞推公式[8]，兩組序列的互信息可表示為

其中X代表時(shí)間序列X(n)，Xτ代表其延遲序列X(n+τ)，H(X)是孤立的 X 的不定性，H(X|Xτ)是已知Xτ的X的不定性，所以Xτ的已知減少了X的不定性，則I(X,Xτ)的第一極小值處的τ即為最佳延遲時(shí)間.并且為了計(jì)算I(X,Xτ)，F(xiàn)raser和Swinney提出了復(fù)雜的劃分網(wǎng)格的方法[2].

互信息I(X,Xτ)表征X和Xτ的相關(guān)程度，相空間重構(gòu)最佳延遲時(shí)間的確定是在保證重構(gòu)坐標(biāo)之間最大限度地相互獨(dú)立的基礎(chǔ)上提出來的.I(X,Xτ)取極小值時(shí)，X和Xτ的相關(guān)度也極小，即X和Xτ的聯(lián)合整體不確定度達(dá)到極大.

另一方面，為了保證重構(gòu)坐標(biāo)之間最大限度地相互獨(dú)立，應(yīng)使X和Xτ聯(lián)合整體的不確定性達(dá)到最大.由信息理論可知，聯(lián)合熵H(X,Xτ)是X和Xτ的聯(lián)合整體的不確定性的度量，H(X,Xτ)越大，則X和Xτ聯(lián)合整體的不確定性也越大.由此推斷，聯(lián)合熵H(X,Xτ)的第一個(gè)極大值點(diǎn)即為相空間重構(gòu)的最佳延遲時(shí)間點(diǎn)[4].

同時(shí)，混沌吸引子在其不變集具有的遍歷特性表現(xiàn)在其狀態(tài)變量X(n)上，即在穩(wěn)態(tài)情況下，對任意的延遲時(shí)間τ，X(n)和X(n+τ)都具有相同的概率分布和統(tǒng)計(jì)特性，則H(X)和H(Xτ)的值接近于常數(shù)，根據(jù)互信息函數(shù)(1)式可推得

可見，H(X,Xτ)和 I(X,Xτ)呈近似相反的變化規(guī)律.互信息的極小值點(diǎn)即為聯(lián)合熵的極大值點(diǎn)在理論上得到驗(yàn)證.

因此通過復(fù)雜的劃分網(wǎng)格或者進(jìn)行網(wǎng)格標(biāo)記求取互信息第一極小值點(diǎn)[6]從而確定相空間重構(gòu)最佳延遲時(shí)間可以轉(zhuǎn)換為求取聯(lián)合熵H(X,Xτ)的第一極大值點(diǎn).聯(lián)合熵的計(jì)算公式[9]可以表示為

由此可見，求取不同延遲時(shí)間下的聯(lián)合熵，找出聯(lián)合熵的第一極大值點(diǎn)所對應(yīng)的τ，即為所求的最佳延遲時(shí)間點(diǎn).

3 符號(hào)分析法求取極大聯(lián)合熵

符號(hào)分析法實(shí)際上是時(shí)間序列的符號(hào)化，該方法是通過在幾個(gè)可能值上將其時(shí)間序列離散化，從而將千變?nèi)f化的數(shù)據(jù)序列轉(zhuǎn)換為幾個(gè)數(shù)值或特殊符號(hào)的符號(hào)序列，該過程稱為粗粒化過程，這一過程能夠從動(dòng)力系統(tǒng)中有效快速地捕獲有用定量信息，并且能夠降低噪聲的影響.將混沌時(shí)間序列通過粗粒化方法轉(zhuǎn)化為符號(hào)序列[10-14]，則其軌道演化的信息就通過符號(hào)序列達(dá)到了編碼.

時(shí)間序列符號(hào)化有二進(jìn)制符號(hào)化規(guī)則、角區(qū)間符號(hào)化規(guī)則和概率統(tǒng)計(jì)符號(hào)化規(guī)則等，二進(jìn)制劃分[13,15]是最簡單的一種劃分規(guī)則，只需給定一個(gè)閾值P0，時(shí)間序列中大于此閾值P0的取1，否則取0.閾值P0的選取有均值，零值等.則時(shí)間序列X(n)最終被轉(zhuǎn)換成符號(hào)序列{S(n)}，所得符號(hào)序列表征了兩種數(shù)據(jù)元模式，即

如圖1所示.

圖1 二進(jìn)制符號(hào)化規(guī)則

二進(jìn)制分割雖然簡便，但是由于其劃分比較粗糙，容易導(dǎo)致原始信息的遺失.為了解決這個(gè)問題，本文通過對相空間的分割從而使時(shí)間序列X(n)實(shí)現(xiàn)粗粒化過程[10-14].以符號(hào)數(shù)取d為例，劃分如下：

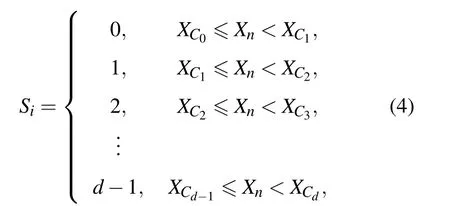
其中Xn為時(shí)間序列X(n)在n時(shí)刻的幅值大小，n=1,2,···,N.XC0,XC1,···,XCd為閾值即臨界點(diǎn)，Si為符號(hào)序列的符號(hào)集，并用相應(yīng)的整數(shù) i來代替，i=0,1,···,d-1. 則時(shí)間序列{X(1),X(2),X(3),···,X(N)} 可以轉(zhuǎn)換成整數(shù)集序列 {S(1),S(2),S(3),···,S(N)}.

時(shí)間序列被轉(zhuǎn)化成長整數(shù)集序列{S(1),S(2),···,S(N)} 后，要提取有用信息，需選擇標(biāo)準(zhǔn)分割長度L.將長整數(shù)集序列分割成長度為L的短序列，L個(gè)連續(xù)符號(hào)被編碼為十進(jìn)制數(shù)，形成了新的整數(shù)集序列表示短序列從長整數(shù)集序列Si的第k個(gè)元素S(k)開始[10].

按照上式進(jìn)行標(biāo)記和辨識(shí)[10-12]，則離散的符號(hào)替代連續(xù)數(shù)據(jù)的原始時(shí)間序列，如圖2所示.

圖2 符號(hào)化時(shí)間序列圖

符號(hào)數(shù)d的個(gè)數(shù)可以通過使符號(hào)熵最大化來尋找[11,12]，為了方便起見，將混沌序列的臨界點(diǎn)(d+1)的個(gè)數(shù)置為11，即d=10.且分割長度L取2.

對時(shí)間序列X(n)及其延遲時(shí)間序列X(n+τ)，n=1,2,···,N，根據(jù)上面所介紹的粗粒化符號(hào)方法將其編碼成能捕獲用定量信息的特殊的十進(jìn)制數(shù)序列Lx(n)和Lxτ(n)，則各個(gè)特殊十進(jìn)制數(shù)出現(xiàn)的頻率為時(shí)間序列分析的指標(biāo)，即為聯(lián)合概率P(Lx,Lxτ)，則符號(hào)分析法求取的聯(lián)合熵[16](3)式可以改寫為

4 數(shù)值仿真試驗(yàn)

為了驗(yàn)證該方法求取最佳延遲時(shí)間的準(zhǔn)確性和優(yōu)越性，我們分別對Lorenz，Rossler和Duf fing三種常見的混沌時(shí)間序列求取最佳延遲時(shí)間并畫出其吸引子的重構(gòu).

Lorenz系統(tǒng)的數(shù)值仿真實(shí)驗(yàn)如圖3所示，Lorenz系統(tǒng)[17]方程

圖3 Lorenz系統(tǒng)(σ=16，b=4，r=45.92)的數(shù)值仿真實(shí)驗(yàn) (a)本文方法和互信息函數(shù)法求取最佳延遲時(shí)間的對比圖;(b)Lorenz吸引子在x-y平面上的投影圖;(c)τ=11時(shí)的Lorenz的重構(gòu)吸引子圖

其中取 σ=16，b=4，r=45.92，此系統(tǒng)為混沌系統(tǒng)，用Runge-Kutta法求解方程(6)，步長h=0.01，取變量x為研究對象，去除前8000個(gè)點(diǎn)，得到一個(gè)7000個(gè)點(diǎn)的時(shí)間序列.通過符號(hào)分析法求取聯(lián)合熵H(Lx,Lxτ)的極大值點(diǎn)和通過網(wǎng)格劃分求取互信息I(X,Xτ)的極小值點(diǎn)的對比圖形如圖3(a)所示，從圖 3(a)可以看出，H(Lx,Lxτ)和 I(X,Xτ)的變化規(guī)律近似相反，并且都是在τ=11時(shí)取得第一個(gè)所對應(yīng)的極值點(diǎn)，故可得由聯(lián)合熵第一極大值點(diǎn)法求得的相空間重構(gòu)最佳延遲時(shí)間達(dá)到了與互信息法相同的效果;試驗(yàn)過程中也大大地簡化了其計(jì)算量.圖3(b)是Lorenz吸引子在x-y平面的投影圖;圖3(c)是τ=11時(shí)的重構(gòu)吸引子圖.從圖中可以看出τ=11時(shí)重構(gòu)圖能夠很好的反映出Lorenz系統(tǒng)的雙圈拓?fù)浣Y(jié)構(gòu).從而驗(yàn)證了符號(hào)分析法求取極大聯(lián)合熵進(jìn)而確定最佳延遲時(shí)間的有效性和優(yōu)越性.

Rossler系統(tǒng)的數(shù)值仿真實(shí)驗(yàn)如圖4所示，Rossler系統(tǒng)[18]方程

其中取 d=0.2，e=0.2，f=0.5，此時(shí) Rossler系統(tǒng)為混沌系統(tǒng)，用Runge-Kutta法求解方程(7)，步長h=0.05，取變量x為研究對象，去除前50000個(gè)點(diǎn)，得到一個(gè)8000個(gè)點(diǎn)的時(shí)間序列.圖4(a)是Rossler系統(tǒng)處于混沌狀態(tài)時(shí)的聯(lián)合熵H(Lx,Lxτ)和互信息I(X,Xτ)的變化規(guī)律圖，兩者的變化成近似相反的規(guī)律，并且在互信息取得極小值點(diǎn)處，聯(lián)合熵處于極大值點(diǎn)，即τ=23;圖4(b)是Rossler吸引子在x-y平面的投影圖;圖4(c)是τ=23時(shí)的重構(gòu)吸引子圖.比較重構(gòu)前后吸引子在x-y平面投影，發(fā)現(xiàn)重構(gòu)吸引子很好地保持Rossler吸引子的單圈結(jié)構(gòu).從而證明了符號(hào)分析法求取聯(lián)合熵極大值點(diǎn)即為最佳延遲時(shí)間的可行性.

圖4 Rossler系統(tǒng)(d=0.2，e=0.2，f=0.5)的數(shù)值仿真實(shí)驗(yàn) (a)本文方法和互信息函數(shù)法求取最佳延遲時(shí)間的對比圖;(b)Rossler吸引子在x-y平面上的投影圖;(c)τ=23時(shí)的Rossler的重構(gòu)吸引子圖

Duf fing系統(tǒng)的數(shù)值仿真實(shí)驗(yàn)如圖5所示，Duffing系統(tǒng)[1]方程

其中取 σ=0.06，a=0.7，F(xiàn)=7.5，此時(shí) Duf fing 系統(tǒng)為混沌系統(tǒng)，用Runge-Kutta法求解方程(8)，步長h=0.05，取變量x為研究對象，舍去開始暫態(tài)點(diǎn)，得到一個(gè)7000個(gè)點(diǎn)的時(shí)間序列.從圖5(a)中能夠明顯看出Duf fing系統(tǒng)此時(shí)的聯(lián)合熵H(Lx,Lxτ)和互信息I(X,Xτ)的近似相反的變化規(guī)律，且由符號(hào)分析法求得的聯(lián)合熵H(Lx,Lxτ)的極大值點(diǎn)為τ=11，與互信息函數(shù)法得到的最佳延遲時(shí)間τ相同.圖5(b)是Duf fing吸引子在x-y平面的投影圖;圖5(c)是τ=11時(shí)的重構(gòu)吸引子圖.比較重構(gòu)前后吸引子在x-y平面投影發(fā)現(xiàn)重構(gòu)效果良好.

圖5 Duf fing系統(tǒng)(σ=0.06，a=0.7，F(xiàn)=7.5)的數(shù)值仿真實(shí)驗(yàn) (a)本文方法和互信息函數(shù)法求取最佳延遲時(shí)間的對比圖;(b)Duf fing吸引子在x-y平面上的投影圖;(c)τ=11時(shí)的Duf fing系統(tǒng)的重構(gòu)吸引子圖

5 結(jié)論

采用符號(hào)分析與極大聯(lián)合熵結(jié)合求取相空間重構(gòu)的最佳延遲時(shí)間，不僅避免了計(jì)算互信息時(shí)的復(fù)雜的網(wǎng)格標(biāo)記，而且無需計(jì)算X(n)和X(n+τ)的各自的概率分布及信息熵.該方法能達(dá)到與互信息方法計(jì)算最佳延遲時(shí)間同樣的效果，而且極大地簡化了計(jì)算，是求取最佳延遲時(shí)間的改進(jìn)算法.理論分析與仿真實(shí)驗(yàn)證明，該方法物理意義明顯，實(shí)際效果較好，能夠更多地保留原系統(tǒng)的動(dòng)力學(xué)特征.

[1]JiangWL，ZhangSQ，WangYQ2005ChaosandWaveletBasedFault Information Diagnosis(Beijing：National Defence Industry Press)p46(in Chinese)[姜萬錄，張淑清，王益群2005基于混沌和小波的故障信息診斷(北京：國防工業(yè)出版社)第46頁]

[2]Fraser A M，Swinney H L 1986 Phys.Rev.A 33 1134

[3]Zhang S Q，Zhao Y C，Jia J，Zhang L G，Shangguan H L 2010 Chin.Phys.B 19 060514

[4]Tian Y C 1997 Systems Engineering Theory and Practice 05 48(in Chinese)[田玉楚1997系統(tǒng)工程理論與實(shí)踐05 48]

[5]Lu X Q，Cao B，Zeng M 2006 Chinese J.Comput Phys.23 184

[6]Zhang J，F(xiàn)an Y Y，Li H M，Sun H Y，Jia M 2011 Chinese J.Comput Phys.28 469(in Chinese)[張菁，樊養(yǎng)余，李慧敏，孫恒義，賈蒙2011計(jì)算物理28 469]

[7]Xiao F H，Yan G R，Han Y H 2005 Acta Phys.Sin.54 0550(in Chinese)[肖方紅，閻桂榮，韓宇航2005物理學(xué)報(bào)54 0550]

[8]Zhang S Q，Jia J，Gao M，Han X 2010 Acta Phys.Sin.59 1576(in Chinese)[張淑清，賈健，高敏，韓敘2010物理學(xué)報(bào)59 1576]

[9]Zhu X K，Jia Y H 2005 Journal of Geomatics 05 3(in Chinese)[祝曉坤，賈永紅2005測繪信息與工程05 3]

[10]Xiao F H，Yan G R，Han Y H 2004 Acta Phys.Sin.53 2877(in Chinese)[肖方紅，閻桂榮，韓宇航2004物理學(xué)報(bào)53 2877]

[11]Lehrman M，Rechester A B 1997 Phys.Rev.Lett.78 54

[12]Rechester A B and White R B 1991 Phys.Lett.A 158 51

[13]Zhang Y 2004 J.Xiangtan Min.Inst.19 75(in Chinese)[張雨 2004湘潭礦業(yè)學(xué)院學(xué)報(bào)19 75]

[14]Azad R K，Rao J S，Ramaswamy R 2002 Chao Solitons and Fractals 14 633

[15]Xiang K，Jiang J P 2007 PR&AI 20 154(in Chinese)[向馗，蔣靜坪2007模式識(shí)別與人工智能20 154]

[16]Shi Y S，Jiang Y，Song Y X 2011 Journal of Aerospace Power 26 670(in Chinese)[史永勝，姜穎，宋云雪2011航空動(dòng)力學(xué)報(bào)26 670]

[17]Yu W B 2008 Calculate Experiment and Analysis on Chaos(Beijing：Science Press)p33(in Chinese)[于萬波2008混沌的計(jì)算實(shí)驗(yàn)與分析(北京：科學(xué)出版社)第33頁]

[18]Liu Z H 2006 Fundamentals and Applications of Chaotic Dynamics(Beijing：Higher Education Press)p71(in Chinese)[劉宗華 2006 混沌動(dòng)力學(xué)基礎(chǔ)及其應(yīng)用(北京：高等教育出版社)第71頁]