弱磁場下三阱光學超晶格中自旋為1的超冷原子特性研究*

秦帥鋒 鄭公平 馬驍 李海燕 童晶晶 楊博

(河南師范大學物理系，新鄉 453007)

(2013年1月6日收到;2013年1月30日收到修改稿)

1 引言

1995年玻色-愛因斯坦凝聚的實驗實現使得超冷原子成為物理學一個非常活躍的研究領域.21世紀初期，超冷原子在超流體和Mott-絕緣體之間的量子相變實驗[1]使得光晶格成為物理學許多研究方向的超低溫實驗室[2].2007年，美國國家標準局的物理學家進一步實現了雙阱光學超晶格[3,4].在雙阱光晶格中，每個雙阱單元中的情況是完全一樣的，在實驗中同時產生了許多完全相同的事例，因此在一次測量過程中就可以得到所觀測量的量子力學期待值[5].基于這個新的試驗方法，實現了許多新奇的現象.Cheinet等通過調節偏壓勢[6]，觀測到雙阱中無自旋原子的粒子數臺階分布，這使得他們可以控制任意某個阱中的原子數.Trotzky等則在對稱的雙阱中通過控制兩個等效自旋為1/2的原子生成了自旋單態與自旋三重態的價鍵態[7]，這對于量子磁性的實驗研究非常有意義.以往的文獻討論光學超晶格中自旋為1的原子的比較少.最近，Wagner等研究了雙阱超晶格中自旋為1的原子數的臺階分布[8].與標量原子和自旋為1/2的原子相比，自旋為1的原子之間具有更豐富的自旋相互作用[9,10].本文中我們將推廣雙阱光學超晶格，提出實現三阱光學超晶格的理論方案，并研究弱磁場下對稱三阱光學超晶格中自旋為1的原子系統的量子多體基態和相圖.由于磁場很弱及三阱之間的關聯，存在許多奇異的自旋態.這些量子態可以通過調節外磁場和光勢壘的高度非常簡便而精確地控制.

2 模型

2.1 三阱光學超晶格

原子感受到的光晶格勢場是由兩束相對傳播的激光束形成的駐波，數學上可描述為

其中V為勢壘高度，λ為晶格周期.本文中考慮一維情況，推廣到三維是直接的.在光晶格勢場的基礎上再疊加一個半周期的光晶格勢，

調節光場強度至4V1＞V2，便可得到對稱雙阱光晶格.若要產生非對稱雙阱光晶格，則需要再加一個磁場梯度.我們發現：如果三個周期比為1：2：3的光晶格勢疊加，

便可形成三阱光晶格.調節至V3=3V1,V2=2V1，三阱光晶格是對稱的，如圖1所示.與雙阱光晶格不同的是，僅僅調節三個勢壘的相對強度，便可實現非對稱三阱光晶格.按照相同的思路，疊加四個周期比為 1：2：3：4 的光晶格勢，還可以實現四阱光晶格.依次類推.

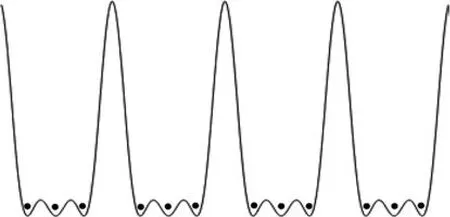
圖1 一維對稱三阱光學超晶格

2.2 三格點Bose-Hubbard模型

考慮超冷的自旋為1的原子囚禁在如圖1所示的一維對稱三阱光學超晶格里，每個三阱單元中囚禁三個原子.由于原子在低勢壘之間的躍遷矩陣元遠大于高勢壘之間的，因此可以將此系統約化為三格點模型，等效的Bose-Hubbard哈密頓量為[8,11,12]

其中

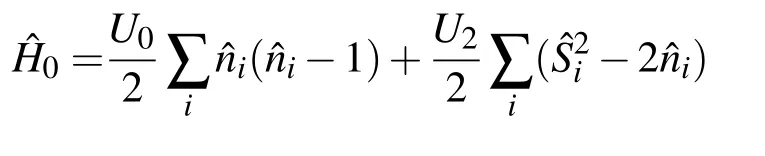
假設外磁場沿著z軸方向，同時也被取為量子化軸方向.考慮弱磁場[14]，參數 p表征線性塞曼能量.約化后的二次塞曼能量q項平移了q，其中是系統的總粒子數算符.采用線性極化微波的方法，參數q的大小和正負已經能夠獨立地調節[15,16].參數U0和U2分別是不依賴和依賴自旋的相互作用常數[17].對于本文考慮的排斥相互作用原子，U0＞0.如果U2＞0或者U2＜0，則自旋相互作用分別是反鐵磁性的，例如23Na，或者鐵磁性的，例如87Rb.對于實驗上常用的原子，|U2|?U0.

3 基態相圖

在圖2中，分別給出了反鐵磁性和鐵磁性原子對應的基態相圖.

圖中Mα表示此態沿量子化軸方向的總自旋分量為α.如圖所示，二者的相圖很不相同.反鐵磁性原子對應的相圖中只可能有M3,M1,M0,M-1,M-3，而鐵磁性原子的相圖中還可能有M±2.在負的q區域，鐵磁性原子的相圖中只有完全極化態M±3.

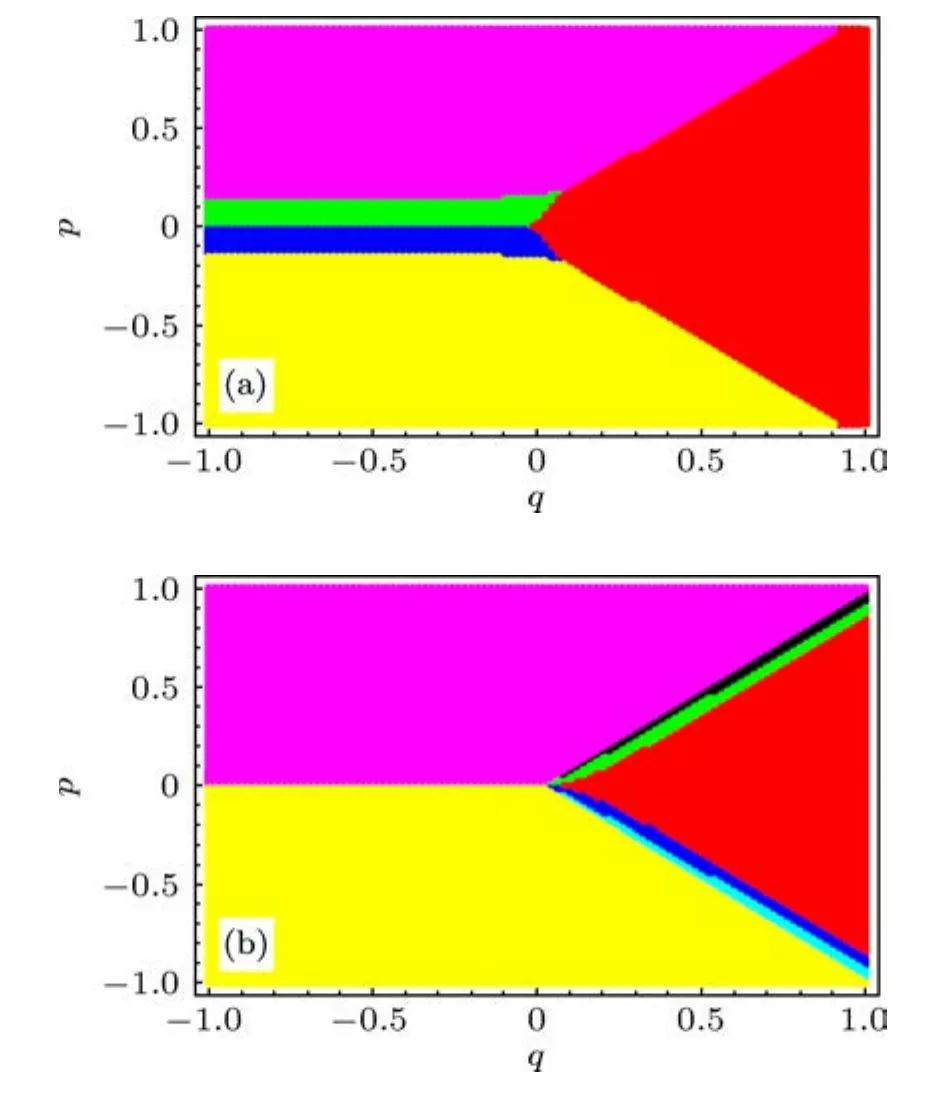
圖2 基態相圖(紫、黑、綠、紅、藍、淺藍、黃色區域分別代表基態M3,M2,M1,M0,M-1,M-2,M-3.參數 p，q均以23Na原子間的U2為單位.鐵磁性原子間依賴自旋的相互作用參數取為-U2.U0=25U2，t=5U2)(a)反鐵磁性23Na原子;(b)鐵磁性原子

這些量子態可以通過調節隧穿參數t和二次塞曼能量q精確地控制.完全極化態M±3的形式為

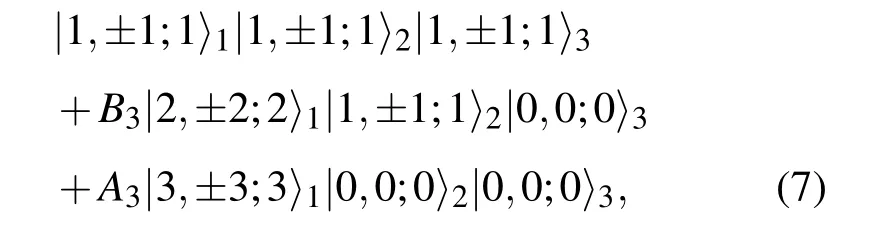
其中右矢態中的三個數字依次表示自旋量子數、磁量子數和原子數目，下標標記格點位置.由于格點位置是可以區分的，因此通過交換下標，另外有五個的本征態與|2,±2;2〉1|1,±1;1〉2|0,0;0〉3是簡并的，在基態中它們是等權疊加的.為了簡化符號，只寫出其中一個.當然，|1,±1;1〉1|1,±1;1〉2|1,±1;1〉3態是唯一的，因為全同量子態不可區分.

基態M±2的形式為

其中A2,B2及態M±3中的A3,B3均隨著隧穿參數t的增大而增大.態M±3和M±2都不受外磁場控制，包括M±2態中的參數β2.但是態M±1為

即M±1與M0同時受隧穿參數t和二次塞曼能量q的控制.下面詳細分析自旋態M0，態M±1有類似的行為.

首先，在圖3給出(10)式中參數B對隧穿參數t的依賴關系.可以看出：無論鐵磁性、反鐵磁性還是中性原子，B都隨著t的減小而減小.參數A有類似的行為.這是因為|U2|?U0，而U0項希望原子在三個格點上均勻分布.隨著t的減小，U0項的影響增大，在弱隧穿極限下，U0項起決定作用，A，B都將趨于零.

(10)式中參數ζ，β，γ，δ更易受二次塞曼能量q的調控.在圖4中，給出了ζ對q的依賴關系.可以看出：無論鐵磁性還是反鐵磁性原子，|ζ|都隨著q的增大而減小.這是因為哈密頓量(3)式中正的q項希望各個格點上的磁量子數為零.隨著q的增大，磁量子數非零的態減少.對于足夠強的二次塞曼能量，鐵磁性或反鐵磁性的自旋為1的原子都趨近于中性原子.出于同樣的原因，參數β有類似的行為.

圖3 基態(10)式中參數B對隧穿參數t的依賴關系(點狀線、實線和虛實線分別對應反鐵磁性、自旋為0的和鐵磁性原子.q=0.5U2，其他參數同圖2)

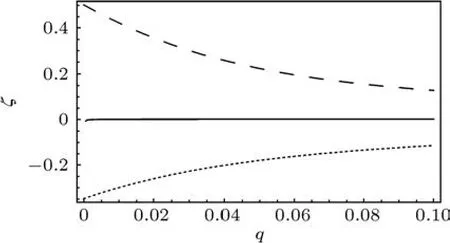
圖4 基態(10)式中ζ對二次塞曼能量q的依賴關系(點狀線、實線和虛實線分別對應反鐵磁性、自旋為0的和鐵磁性原子.t=2.5U2，其他參數同圖2)

圖5給出了δ對q的依賴關系.對于反鐵磁性原子，自旋相互作用U2項希望基態下總自旋量子數Stotal盡可能的小，而鐵磁性原子的選擇正好相反.正的q項希望各個格點上的磁量子數為零，但它僅僅是希望磁量子數為零，不管Stotal是大還是小.隨著q的增大，自旋相互作用U2項的作用被弱化，因此對于鐵磁性原子δ會減小，而對于反鐵磁性原子δ將增大.參數γ有類似的行為.

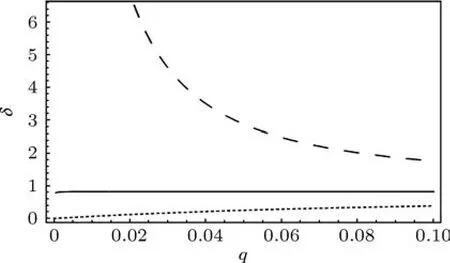
圖5 基態(10)式中δ對二次塞曼能量q的依賴關系(點狀線、實線和虛實線分別對應反鐵磁性、自旋為0的和鐵磁性原子.參數同圖4)

4 結論

本文從理論上研究了弱磁場下對稱三阱光學超晶格中自旋為1的超冷原子系統的基態.三阱光學超晶格具有與雙阱光學超晶格相同的優點：在實驗中可以同時產生許多完全相同的事例.同時相對于雙阱光學超晶格中的兩格點關聯，三格點關聯具有更豐富的物理內容.并且由于這些量子自旋態可以通過調節外磁場和光勢壘的高度非常簡便而精確地控制，因此適合用來進一步研究自旋糾纏[8,19-21].

[1]Greiner M，Mandel O，Esslinger T，H¨ansch T W，Bloch I 2002 Nature 419 51

[2]Lewenstein M，Sanpera A，Ahu finger V，Damski B，Sen A，Sen U 2007 Advances in Physics 56 243

[3]Sebby-Strabley J，Anderlini M，Jessen P S，Porto J V 2006 Phys.Rev.A 73 033605

[4]Anderlini M，Lee P J，Brown B L，Sebby-Strabley J，Phillips W D，Porto J V 2007 Nature 448 452

[5]F¨olling S，Trotzky S，Cheinet P，Feld M，Saers R，Widera A，M¨uller T，Bloch I 2007 Nature 448 1029

[6]Cheinet P，Trotzky S，Feld M，Schnorrberger U，Moreno-Cardoner M，F¨olling S，Bloch I 2008 Phys.Rev.Lett.101 090404

[7]Trotzky S，Chen Y A，Schnorrberger U，Cheinet P，Bloch I 2010 Phys.Rev.Lett.105 265303

[8]Wagner A，Bruder C，Demler E 2011 Phys.Rev.A 84 063636

[9]Zhang Y B，Harri M，Kalle-Antti S 2005 Chin.Phys.Lett.22 536

[10]Pang W，Li Z B，Bao C G 2007 Chin.Phys.Lett.24 2745

[11]Chen B L，Kou S P，Zhang Y B，Chen S 2010 Phys.Rev.A 81 053608

[12]Liang J Q，Liu J L，Li W D，Li Z J 2009 Phys.Rev.A 79 033617

谷氨酸鈉是味精的主要成分及增味成分；I+G又稱為核苷酸二鈉，是由5'-肌苷酸二鈉(IMP)和5'-鳥苷酸二鈉(GMP)按1∶1的比例混合而成，是一種新型的核苷酸類食品增味劑。趙燕華等[24]研究表明該類型增味劑復合使用可增加肉丸的肉質感且穩定性好，能保持42 h以上不產生不良氣味。王向陽等[25]研究發現，谷氨酸鈉和I+G的耐熱性和耐酸性較弱，因此在肉制品加工過程中要避免高溫及酸性環境。

[13]Pethick C J，Smith H 2002 Bose-Einstein Condensation in Dilute Gases(Cambridge：Cambridge University Press)p331

[14]Zheng G P，Tong Y G，Wang F L 2010 Phys.Rev.A 81 063633

[15]Gerbier F，Widera A，F¨olling S，Mandel O，Bloch I 2006 Phys.Rev.A 73 041602

[16]Ueda M 2012 Annu.Rev.Condens.Matter Phys.3 263

[17]Ho T L 1998 Phys.Rev.Lett.81 742

[18]Demler E，Zhou F 2002 Phys.Rev.Lett.88 163001

[19]Hao Y J，Liang J Q 2006 Chin.Phys.15 1161

[20]YanD，Song L J，Chen D W 2009 Acta Phys.Sin.58 3679(in Chinese)[嚴冬，宋立軍，陳殿偉2009物理學報58 3679]