接觸角與液固界面熱阻關系的分子動力學模擬*

葛宋 陳民

(清華大學工程力學系，北京 100084)

(2012年11月9日收到;2013年1月30日收到修改稿)

1 引言

在微納機電系統中由于尺度的減小導致面體比顯著增大，界面效應往往變得不可忽略甚至可能成為主導因素[1].液固界面處的界面熱阻及由此產生的界面溫度跳躍是重要的界面現象[2]，其對微納米系統中能量傳遞的影響可由熱阻長度來判斷.熱阻長度表征的是在液體內部形成與界面溫度跳躍相同的溫度差所需的液體層厚度[3].實驗和模擬結果都表明在較疏水的液固界面，熱阻長度可達到數十納米[4,5].表面濕潤性也是一種重要的界面性質，而靜態接觸角是衡量表面濕潤性的主要物理量.相比于界面熱阻，目前對于表面濕潤性和接觸角的研究更加充分.一方面表征固體表面濕潤性的接觸角在宏觀實驗中容易測量，另一方面，現有的材料加工技術已能方便地制造出具有不同濕潤性的表面[6-8].界面熱阻和表面濕潤性作為兩種重要的界面現象，如果能建立起界面熱阻和接觸角之間的聯系，將為微納米系統中的材料選擇和熱設計提供極大的便利.已有學者注意到液固界面熱阻與表面濕潤性的聯系，并試圖建立起接觸角和界面熱阻的函數關系[9-11].Murad和Puri[9]推斷親水的表面將有利于減小液固界面熱阻.Shenogina等[11]利用在水和不同化學成分的固體表面構成的界面上的模擬結果提出界面熱導G(界面熱阻的倒數)與接觸角之間存在如下關系：G=B(1+cosθ)，其中B為比例系數，θ為接觸角，但此關系式的適用性還有待進一步驗證.本文利用分子動力學方法模擬了液體在固體表面的接觸角及相同條件下的液固界面熱阻，探討了兩者之間的關系，有助于加深對界面熱阻產生機理的理解，同時能為實際應用提供理論參考.

2 模擬方法與細節

2.1 接觸角的模擬方法

接觸角的模擬系統如圖1所示.本文中所有粒子間的相互作用均采用12-6 Lennard-Jones(LJ)勢能函數來描述：

其中σ為分子直徑，ε為能量參數，r為原子之間的距離.模型液體為氬，分子直徑σ=3.405×10-10m，能量參數ε=1.67×10-21J.采用LJ模型固體.由于LJ模型固體熔點正比于固體原子間相互作用的能量參數εSS(約為0.5εSS/kB，kB為玻爾茲曼常數)，模擬中將εSS取得足夠大以使其在模擬中能始終保持固態.此模型不需要引入彈簧力來維持固態，能較真實地描述固體的熱學性質[4].固體原子的直徑與氬原子相同.固體壁面由7層按fcc晶格結構排列的原子構成，晶格常數為a0=1.56σ，其(1，0，0)面與氬液滴及氬蒸汽相接觸.最底層的原子在模擬中保持固定.

圖1 接觸角的模擬體系

模擬系統在三個方向上均使用周期性邊界條件，模擬的是二維液滴.模擬盒子的尺寸為100 a0×10 a0×45 a0，x和z方向的尺度顯著大于y方向.模擬體系中包含7200個氬原子和14000個壁面原子.液滴在平衡后的直徑大于10 nm，這樣能保證獲得的接觸角受尺度效應的影響較小.模擬中體系的演化采用速度Verlet算法，截斷半徑取為1 nm，積分步長為5 fs.通過Langevin熱浴來控制體系的溫度.模擬的前250萬步用來使體系達到平衡，然后對位形進行取樣來統計液體的密度分布.每100步取樣一次，共獲得多于5000個樣本.將模擬盒子在xz平面內劃分成網格，網格的大小為1?A×1?A，以此獲得體系的密度分布.將液滴密度和蒸汽密度之和的二分之一的等密度線視為液滴的邊界[12]來獲得液滴的輪廓.同Leroy等[13]的做法相同，本文利用液滴輪廓的高度h和基線長度b來計算接觸角，如圖2所示.由于液體在液固界面的分層現象，我們將基線的位置取在離固體第一層原子距離為d=σ處[14].

2.2 液固界面熱阻的模擬方法

液固界面熱阻的模擬體系如圖3所示，由兩個相等的液體區域及中間的固體區域構成.模擬盒子的尺寸為10 a0×10 a0×56 a0，其中固體區域為10 a0×10 a0×19 a0.液體區域的密度保持與接觸角模擬中的液體密度相同.固體模型與接觸角模擬中的固體壁面模型相同.

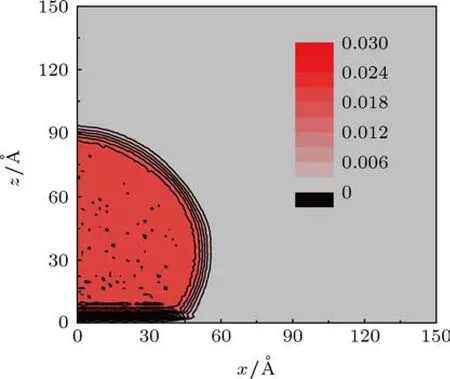
圖2 接觸角的計算方法

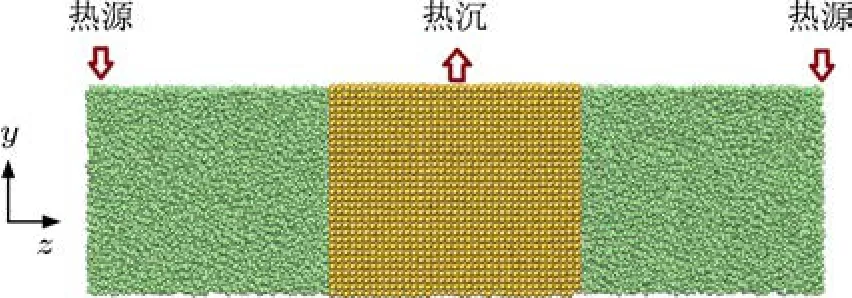
圖3 液固界面熱阻的模擬體系

三個方向均采用周期性邊界條件.截斷半徑取為1 nm，步長取為0.5 fs，能使體系的能量保持守恒.為了防止固體區域產生移動，在模擬中每隔10步去掉固體區域質心的動量.首先利用控溫使體系在設定的溫度下達到平衡，隨后將控溫移除，在固體和液體的圖示區域分別設置熱源和熱沉，在熱源中不斷輸入熱量，在熱沉中移走熱量.這是通過增加或減小相應區域原子的動能來實現的.體系整體將保持能量守恒.平衡后，體系中將建立起穩定的溫度分布，界面溫度跳躍ΔT及熱流q.將體系沿z方向劃分成條狀區域，區域的寬度為a0，統計各區域中的溫度即可獲得溫度分布和界面溫度跳躍.每一步加入的熱量為ΔE，體系中的熱流為q=ΔE/(2AΔt)=620 MW/m2.(其中A為模擬體系在xy平面的截面積，Δt為時間步長，分母中的因子2來源于體系的對稱性).液固界面熱阻R或界面熱導G則可由定義R=ΔT/q和G=q/ΔT來分別獲得.

為了獲得接觸角和界面熱阻的關系，我們通過如下方法來改變固液界面的性質及固體的性質并檢驗二者的關系：1)保持固體的性質不變，調整液固間相互作用的勢能參數εSL來改變液固間相互作用強度;2)保持液固間相互作用勢能參數εSL不變，調整固體的性質.

3 結果與討論

3.1 接觸角

楊氏方程描述了接觸角θ與液固表面張力γLS，液氣表面張力γLV以及氣固表面張力γSV之間的關系[15]：

引入黏附功H12的概念，其表征的是分開單位面積的液固界面所需做的功.界面黏附功H12也可由表面張力來表示：

聯系(2)式和(3)式可見存在如下關系：

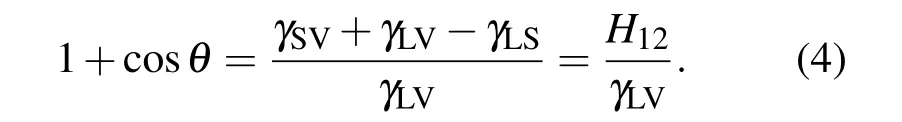
同時，假定固體和液體均勻分布，黏附功H12可近似表述為[16]

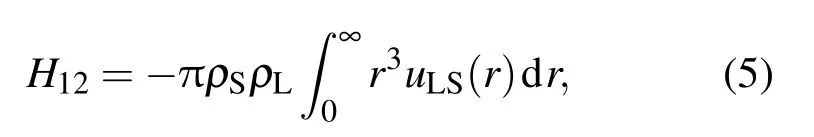
其中ρS，ρL分別為固體和液體的數密度，uLS為液固分子間勢能函數.對于采用的12-6 Lennard-Jones勢能，黏附功H12正比于勢能參數εLS：H12∝εSL[16].當液體的種類給定時，γLV為常數.將(5)式代入(4)式：

可見液固界面相互作用強度是決定接觸角的主要物理量，且當固體的晶格排列方式固定時，接觸角將不受固體原子質量和固體原子之間相互作用強度的影響.

利用分子動力學模擬來驗證上述推論.首先考慮液固間相互作用的影響.保持固體的性質不變(此時令 mS=0.75mAr，εSS=10εAr)，調整液固間相互作用的勢能參數εLS來改變液固間相互作用強度.模擬得到的接觸角θ隨液固相互作用強度的變化如圖4所示，圖4中的插入圖還給出了接觸角的余弦值.可見接觸角θ隨εSL的增大而減小，即親水性增加，并且1+cosθ與液固相互作用強度εSL較好地滿足線性關系，與理論分析給出的(6)式及文獻中的模擬結果[15]符合.

圖4 不同液固相互作用強度下的接觸角

保持液固間相互作用勢能參數εSL=0.5εAr不變，調整固體的性質 (保持 mS=0.75mAr，εSS從 6εAr增大到 14εAr;或保持 εSL=10εAr，mS從 20 amu 增大到80 amu)來模擬對接觸角的影響.固體原子間相互作用強度εSS和固體原子質量mS對接觸角的影響如圖5所示.兩者對接觸角產生的影響均在±4%以內.這也與前面的理論分析結果一致.

3.2 液固界面熱阻與接觸角的關系

分析不同因素(液固間相互作用強度，固體原子質量及固體原子間相互作用強度)對界面熱阻的影響.液固間相互作用強度是影響液固界面能量傳遞的重要因素[17].先考慮液固間相互作用的影響：保持固體的性質不變，調整固液間相互作用強度 (能量參數 εLS由 0.4εAr增大到 2.4εAr，此時表面由疏水變化到親水).模擬結果顯示，界面熱導隨液固間相互作用強度增大而增大，如圖6所示.顯然液固間相互作用強度的增加促進了界面處的能量傳遞，這與文獻的模擬結果一致[10,17].

保持液固間相互作用勢能參數εSL=0.5εAr不變，改變固體原子質量mS或固體原子間能量參數εSS，固體的力學性質和熱學性質如聲速，熱振動頻率等都會改變.分別驗證這兩個因素對界面熱阻的影響.保持固體原子質量不變，εSS從6εAr增大到14εAr;或保持εSS=10εAr不變，將固體原子質量 mS從20 amu增大到80 amu，界面熱導的變化如圖7所示.

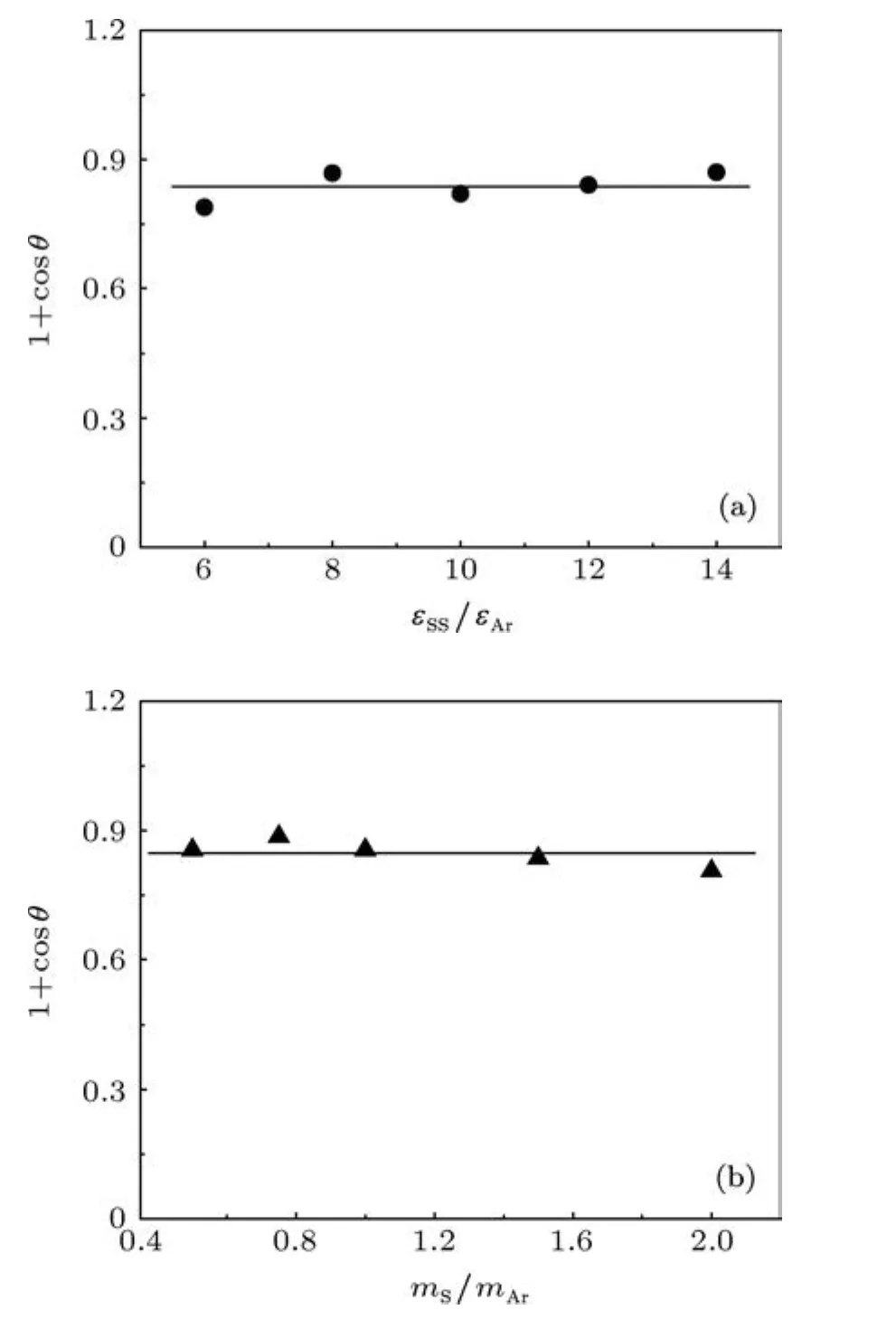
圖5 固體性質對接觸角余弦的影響 (a)能量參數εSS;(b)固體原子質量mS

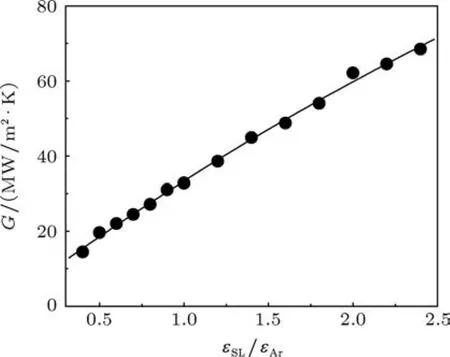
圖6 液固界面熱導隨液固間相互作用強度的變化

由圖7可見，在保持液固間相互作用不變的情況下，固體的性質對界面熱阻(界面熱導)有重要的影響，且mS與εSS有相反的作用.我們從液固原子間振動耦合的角度來分析固體間原子結合強度與原子質量對液固界面熱阻產生影響的原因.

液固原子間的振動耦合越好，即兩種原子的振動頻率分布的重合程度越好，更多的能量將以簡諧振動的方式傳遞，界面熱阻將越小[18,19].原子熱振動頻率與原子質量和原子間結合強度近似存在如下關系：ω∝(εSS/mS)1/2.相較于固體而言，由于液體原子間較弱的結合力，液體原子的振動分布在較低的頻率范圍內[20]，而固體原子將在較高的頻率內間振動，兩者間存在一定的重合.此頻率重合程度即決定了液固原子間的振動耦合度.固體原子質量和固體間相互作用強度對振動耦合度的影響，可從原子的振動態密度的角度來分析.

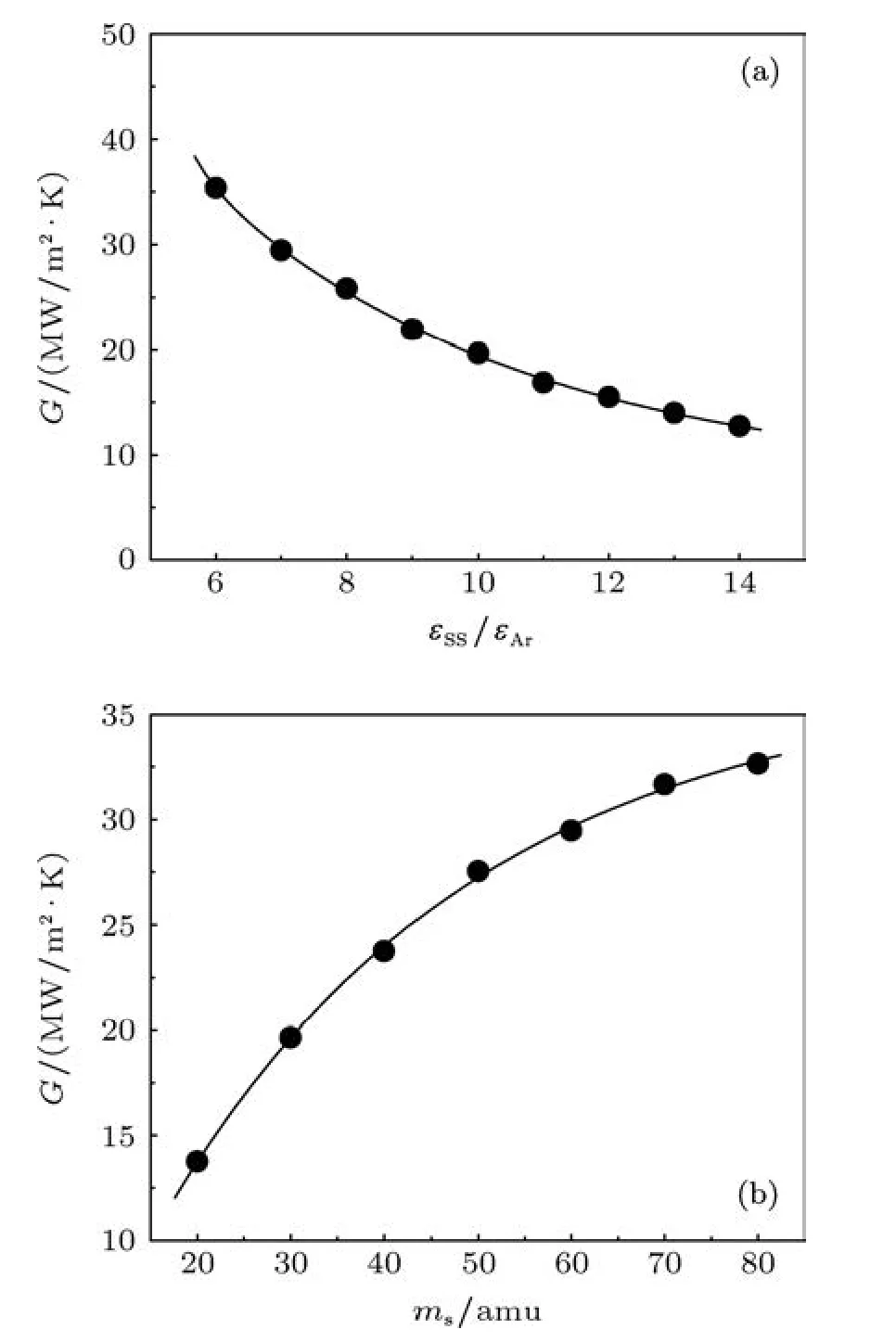
圖7 固體性質對界面熱導的影響 (a)能量參數εSS;(b)固體原子質量mS

利用原子的速度自相關函數(velocity autocorrelation fuction，VACF)可獲得貼壁液體層，界面固體層的振動態密度(vibrational density of state，VDOS)，其表征了原子振動的頻率分布.速度自相關函數定義為

其中v為原子的速度，〈〉代表對不同時間原點的統計平均.原子的振動態密度可由速度自相關函數的傅里葉變換獲得

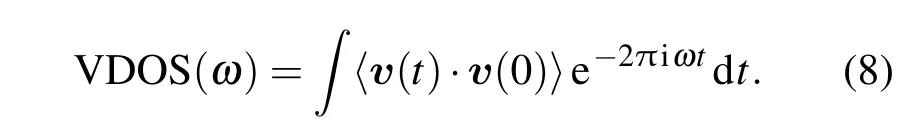
計算得到的不同固體原子質量下的振動態密度分布如圖8(a)和(b)所示.對比圖8(a)和(b)，顯然，增大固體原子質量時固體原子振動的頻率分布向低頻率移動，增大了界面處液固間振動頻率的重合程度，即圖中重合區域面積增大，界面熱導將隨之增大;類似地也能得出，增強固體原子間相互作用強度將使固體原子的振動向高頻率區移動，此時界面處液固間的振動頻率重合程度降低，將使得界面熱導減小.這個模擬結果與前面的預測是一致的.

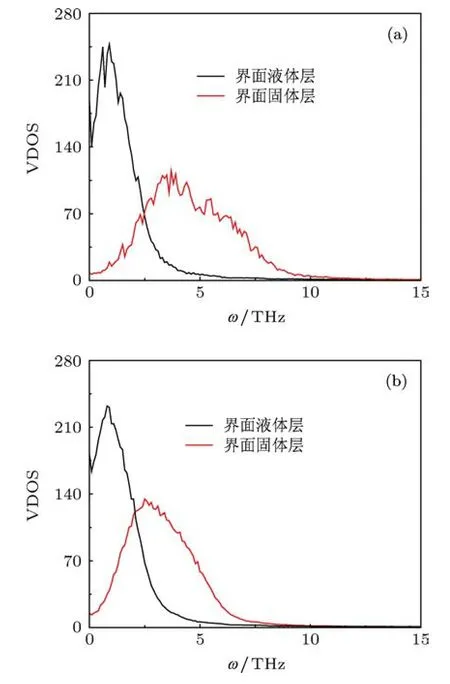
圖8 原子振動的態密度分布 (a)mS=0.5mAr;(b)mS=mAr

根據接觸角和界面熱導隨不同因素的變化趨勢，可歸納出接觸角與界面熱導間的關系，如圖9所示.如果只改變液固間相互作用強度，界面熱導G與接觸角θ的余弦間存在近似的線性關系，這與Shenogina等[11]提出的G=B(1+cosθ)關系相符(其中B為比例系數).但是當接觸角不變，固體原子質量與原子間相互作用強度改變時，界面熱導的變化與接觸角的余弦近似無關.因此界面熱導與接觸角不存在單值對應關系，液固界面熱阻間與接觸角之間也不存在單值的對應關系.

圖9 改變不同參數時界面熱導與接觸角的關系

4 結論

本文利用分子動力學方法分別模擬了液體在固體表面的接觸角及液固界面熱阻，并探討了二者間的聯系.分別通過改變液固間相互作用強度和固體的性質來分析接觸角和界面熱阻的變化趨勢.模擬結果顯示接觸角隨液固間相互作用增強而減小，接觸角的余弦與液固間的相互作用能量參數呈線性關系，但接觸角并不受固體原子質量和固體間相互作用強度的影響.另一方面，界面熱阻隨液固間相互作用增強而減小;同時，在液固相互作用強度不變的情況下，固體原子間結合強度與固體原子質量對界面熱阻有顯著影響，這是由于這兩個因素導致固體的振動頻率發生變化，使得液固原子間的振動耦合度改變，從而使得界面熱阻改變.本文的模擬表明，界面熱阻與接觸角間不存在單值對應關系，不能單一地將接觸角作為液固界面熱阻的評價標準.

本文的計算在清華大學信息科學與技術國家實驗室(籌)的高性能計算平臺上完成.

[1]Cahill D G，Ford W K，Goodson K E，Majumdar A，Mariset H J，Merlin R，Phillpot S R 2010 J.Appl.Phys.93 793

[2]Swartz E T，Pohl R O 1989 Rev.Mod.Phys.61 605

[3]Barrat J L，Chiaruttini F 2003 Mol.Phys.101 1605

[4]Xue L，Keblinski P，Phillipot S R，Choi S U S，Eastman J A 2003 J.Chem.Phys.118 337

[5]Ge Z B，Cahill D G，Braun P V 2006 Phys.Rev.Lett.96 186101

[6]Gu C Y，Di Q F，Shi L Y，Wu F，Wang W C，Yu Z B 2008 Acta Phys.Sin.57 3071(in Chinese)[顧春元，狄勤豐，施利毅，吳非，王文昌，余祖斌2008物理學報57 3071]

[7]Ma H M，Hong L，Yin Y，Xu J，Ye H 2011 Acta Phys.Sin.60 098105(in Chinese)[馬海敏，洪亮，尹伊，許堅，葉輝 2011物理學報 60 098105]

[8]Gong M G，Xu X L，Cao Z L，Liu Y Y，Zhu H M 2009 Acta Phys.Sin.58 1885(in Chinese)[公茂剛，許小亮，曹自立，劉遠越，朱海明2009物理學報58 1885]

[9]Murad S，Puri I K 2008 Appl.Phys.Lett.92 133105

[10]Wang Y，Keblinski P 2011 Appl.Phys.Lett.99 073112

[11]Shenogina N，Godawat R，Keblinski P，Garde S 2009 Phys.Rev.Lett.102 156101

[12]Shi B，Dhir V K 2009 J.Chem.Phys.130 034705

[13]Leroy F，M¨uller-Plathe F 2010 J.Chem.Phys.133 044110

[14]Voronov R S，Papavassiliou D V，Lee L L 2006 J.Chem.Phys.124 204701

[15]Sedlmeier F，Janecek J，Sendner C，Bocquet L，Netz R R，Horinek D 2008 Biointerphases 3 23

[16]Rowlinson J，WidomB 1982 Molecular Theory of Capillarity(Oxford：Oxford University Press)p86

[17]Maruyama S，Kimura T 1999 Therm.Sci.Eng.7 63

[18]Kikugawa G，Ohara T，Kawaguchi T，Torigoe E，Hagiwara Y，Matsumoto Y 2009 J.Appl.Phys.130 074706

[19]Issa K M，Mohamad A A 2012 Phys.Rev.E 85 031602

[20]Huxtable S T，Cahill D G，Shenogin S，Keblinski P 2005 Chem.Phys.Lett.407 129