鐵路編組站配流與調(diào)機(jī)運(yùn)用的協(xié)調(diào)決策優(yōu)化

薛 鋒，陳崇雙，戶(hù)佐安

1.西南交通大學(xué) 交通運(yùn)輸與物流學(xué)院，成都610031

2.北京交通大學(xué) 軌道交通控制與安全國(guó)家重點(diǎn)實(shí)驗(yàn)室，北京100044

1 引言

鐵路編組站的調(diào)度指揮工作是通過(guò)編制與執(zhí)行階段計(jì)劃來(lái)完成的。階段計(jì)劃（3～4 小時(shí)）是班計(jì)劃（12 小時(shí)）分階段的具體安排，主要解決本階段內(nèi)所有列車(chē)的出發(fā)計(jì)劃、調(diào)機(jī)運(yùn)用計(jì)劃和到發(fā)線(xiàn)運(yùn)用計(jì)劃三個(gè)決策問(wèn)題，其中第一個(gè)子問(wèn)題確定出發(fā)列車(chē)的編組內(nèi)容和車(chē)流來(lái)源（即配流），第二個(gè)子問(wèn)題確定每臺(tái)調(diào)機(jī)的調(diào)車(chē)工作內(nèi)容和時(shí)段，第三個(gè)子問(wèn)題安排到發(fā)列車(chē)占用到發(fā)線(xiàn)計(jì)劃。只有合理運(yùn)用調(diào)機(jī)，正確地組織解編作業(yè)，才能加速調(diào)車(chē)場(chǎng)的車(chē)流集結(jié)過(guò)程，縮短車(chē)輛在站停留時(shí)間，實(shí)現(xiàn)列車(chē)的出發(fā)計(jì)劃，因而調(diào)機(jī)運(yùn)用與列車(chē)配流密不可分，而第三個(gè)問(wèn)題則相對(duì)獨(dú)立[1]。如何合理地運(yùn)用調(diào)機(jī)全面完成配流計(jì)劃，是值得研究的問(wèn)題。在技術(shù)站中，由于區(qū)段站調(diào)機(jī)設(shè)備少，往往使接續(xù)時(shí)間合理的車(chē)流因調(diào)機(jī)的繁忙而難于實(shí)現(xiàn)，一些專(zhuān)家學(xué)者在研究區(qū)段站的配流問(wèn)題時(shí)都緊密結(jié)合調(diào)機(jī)來(lái)建模和求解[2-3]。編組站雖然調(diào)機(jī)配備較多，且解體和編組作業(yè)由不同的調(diào)機(jī)擔(dān)當(dāng)，但仍需以配流計(jì)劃為核心，合理決策，使列車(chē)配流與調(diào)機(jī)運(yùn)用相協(xié)調(diào)。本文根據(jù)編組站的實(shí)際作業(yè)特點(diǎn)，構(gòu)造了配流與調(diào)機(jī)運(yùn)用的協(xié)調(diào)優(yōu)化模型，以期實(shí)現(xiàn)編組站車(chē)流資源的合理分配。

2 參數(shù)定義

設(shè)T0為階段計(jì)劃開(kāi)始時(shí)刻，在階段計(jì)劃時(shí)間內(nèi)的出發(fā)列車(chē)的車(chē)流來(lái)源包括[4]：

（1）T0時(shí)刻已解入調(diào)車(chē)場(chǎng)集結(jié)等待編組的現(xiàn)車(chē)，可視作1 列到達(dá)列車(chē)。

（2）T0時(shí)刻到達(dá)場(chǎng)內(nèi)待解列車(chē)車(chē)流。

（3）階段時(shí)間內(nèi)預(yù)計(jì)將要到達(dá)列車(chē)車(chē)流。

（4）交換場(chǎng)等待轉(zhuǎn)場(chǎng)分解的車(chē)組，每轉(zhuǎn)場(chǎng)一次視作1 列到達(dá)列車(chē)。

（5）貨場(chǎng)、專(zhuān)用線(xiàn)、車(chē)輛段取回待分解的本站作業(yè)車(chē)、修竣車(chē)，每取回一次視作到達(dá)一列。

設(shè)本階段到達(dá)解體列車(chē)數(shù)為n，到達(dá)解體列車(chē)（含調(diào)車(chē)場(chǎng)現(xiàn)車(chē)）集合按到達(dá)時(shí)間先后記作DD={dd0,dd1,…,ddi,…,ddn}；將要編組出發(fā)的列車(chē)（不包括已編完的待發(fā)列車(chē)）數(shù)為m，編組出發(fā)列車(chē)集合按出發(fā)時(shí)間先后記作CF={cf1,cf2,…,cfj,…,cfm}；車(chē)站共有K個(gè)編組去向，構(gòu)成編組去向集合QX={1,2,…,K}；車(chē)站共有D臺(tái)調(diào)機(jī)，構(gòu)成集合DJ={1,2,…,D}。對(duì)于到達(dá)解體列車(chē)ddi(i=1,2,…,n，其到達(dá)時(shí)刻為T(mén)idd；開(kāi)始解體時(shí)刻為T(mén)ijt；列車(chē)ddi中具有本站編組去向號(hào)k(1 ≤k≤K)的車(chē)數(shù)為ddik；對(duì)于出發(fā)列車(chē)cfj(j=1,2,…,m)，其出發(fā)時(shí)刻為；開(kāi)始編組時(shí)刻為；已編組列車(chē)cfj中具有本站編組去向號(hào)k(1 ≤k≤K)的車(chē)數(shù)為cfjk。列車(chē)解體作業(yè)時(shí)間標(biāo)準(zhǔn)為tjt，編組作業(yè)時(shí)間標(biāo)準(zhǔn)為tbz，到達(dá)列車(chē)技術(shù)作業(yè)時(shí)間標(biāo)準(zhǔn)為tdd，出發(fā)列車(chē)技術(shù)作業(yè)時(shí)間標(biāo)準(zhǔn)為tcf；表示調(diào)機(jī)d的第s(1 ≤s≤Sd)項(xiàng)固定作業(yè)的開(kāi)始時(shí)刻，其中Sd為調(diào)機(jī)d總的固定作業(yè)項(xiàng)數(shù)；表示調(diào)機(jī)d的第s項(xiàng)固定作業(yè)的作業(yè)時(shí)間；出發(fā)列車(chē)cfj的滿(mǎn)軸車(chē)數(shù)為mj，配流時(shí)的方案值為Fj。

定義布爾變量：φid、φjd、λij、βj。若到達(dá)列車(chē)ddi(i=1,2,…,n)由調(diào)機(jī)d(1 ≤d≤D)解體，則φid取1，否則為0；若出發(fā)列車(chē)cfj(j=1,2,…,m) 由調(diào)機(jī)(1 ≤d≤D) 編組，則φjd取1，否則為0；若出發(fā)列車(chē)cfj能接續(xù)到達(dá)列車(chē)ddi，則λij取1，否則為0；若Fj≥0，則βj取1，否則為0。

定義決策變量：cfijk表示到達(dá)列車(chē)ddi(i=0,1,…,n)配入出發(fā)列車(chē)cfj(j=1,2,…,m)編組去向號(hào)k(1 ≤k≤K)的車(chē)數(shù)。

3 模型構(gòu)造

3.1 配流約束

設(shè)M表示充分大的正數(shù)，則配流的約束條件為：

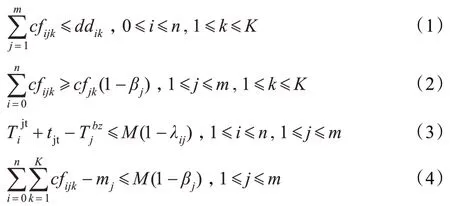
式（1）界定了出發(fā)列車(chē)中同一去向車(chē)流的配流上限；式（2）表示出發(fā)列車(chē)的基本去向組輛數(shù)約束；式（3）表示車(chē)流接續(xù)時(shí)間約束；式（4）表示列車(chē)編組輛數(shù)約束。

3.2 解體約束

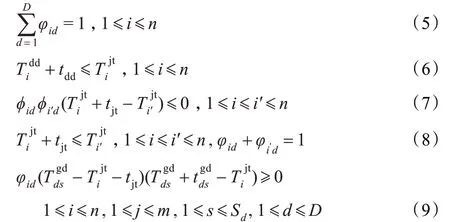
式（5）表示任一列到達(dá)解體列車(chē)只能由一臺(tái)調(diào)機(jī)解體；式（6）表示到達(dá)列車(chē)解體時(shí)須完成到達(dá)技術(shù)作業(yè)；式（7）表示若兩列到達(dá)列車(chē)由同一臺(tái)調(diào)機(jī)解體，在時(shí)間上不能沖突；式（8）表示雙推單溜時(shí)，只有當(dāng)前一列車(chē)解體完畢，另一列車(chē)才能開(kāi)始解體；式（9）表示到達(dá)列車(chē)的解體作業(yè)與解體調(diào)機(jī)的固定作業(yè)不沖突。

3.3 編組約束

式（10）表示任一列出發(fā)列車(chē)只能由一臺(tái)調(diào)機(jī)編組；式（11）表示出發(fā)列車(chē)的最晚編組時(shí)刻須滿(mǎn)足技術(shù)作業(yè)時(shí)間要求，以保證正點(diǎn)發(fā)車(chē)；式（12）表示若兩列出發(fā)列車(chē)由同一臺(tái)調(diào)機(jī)編組，在時(shí)間上不能沖突；式（13）表示2 臺(tái)調(diào)機(jī)編組時(shí)占用同一牽出線(xiàn)不沖突；式（14）表示出發(fā)列車(chē)的編組作業(yè)與編組調(diào)機(jī)的固定作業(yè)不沖突。

3.4 目標(biāo)函數(shù)

編組站調(diào)機(jī)運(yùn)用計(jì)劃的安排是為列車(chē)合理配流服務(wù)的，而配流的最終目的是為了確保出發(fā)列車(chē)的滿(mǎn)軸和正點(diǎn)。約束式（1）～式（14）的可行域保證了出發(fā)列車(chē)的正點(diǎn)，因此目標(biāo)函數(shù)可設(shè)定為滿(mǎn)軸列車(chē)數(shù)最多。

s.t. 式（1）～式（14）

式（15）表示盡可能使?jié)M軸的出發(fā)列車(chē)數(shù)最多，即欠軸列車(chē)數(shù)最少。至此，構(gòu)造了基于列車(chē)配流和調(diào)機(jī)運(yùn)用約束的協(xié)調(diào)決策優(yōu)化模型。一般情況下，編組站解體和編組作業(yè)由不同的調(diào)機(jī)擔(dān)當(dāng)，二者在作業(yè)互不干擾，具有相對(duì)獨(dú)立性，關(guān)鍵是列車(chē)的解體和編組方案決定了出發(fā)列車(chē)的配流方案，即只有在解體、編組方案確定的情況下，才能實(shí)現(xiàn)對(duì)配流問(wèn)題的優(yōu)化。由于調(diào)機(jī)的運(yùn)用和配流方案密切相關(guān)，所以確定到達(dá)列車(chē)的解體順序方案和出發(fā)列車(chē)的編組順序方案需要考慮調(diào)機(jī)的數(shù)量和調(diào)機(jī)作業(yè)方式，解體和編組時(shí)刻的具體計(jì)算公式可參考文獻(xiàn)[5]。

4 模型的遺傳算法求解

列車(chē)配流和調(diào)機(jī)運(yùn)用約束的協(xié)調(diào)決策優(yōu)化模型，其復(fù)雜性為NP 難題，不可能得到求其最優(yōu)解的多項(xiàng)式算法。編組站列車(chē)配流與調(diào)機(jī)運(yùn)用的協(xié)調(diào)決策問(wèn)題對(duì)算法收斂速度有著較強(qiáng)的實(shí)時(shí)性要求，需要根據(jù)問(wèn)題的性質(zhì)提出新的啟發(fā)式算法。遺傳算法是一種以自然選擇和遺傳理論為基礎(chǔ)，將生物進(jìn)化過(guò)程中適者生存規(guī)則與種群內(nèi)部染色體的隨機(jī)信息交換機(jī)制相結(jié)合的優(yōu)化搜索算法，它已經(jīng)被成功地引入編組站作業(yè)優(yōu)化領(lǐng)域用于解決大規(guī)模組合優(yōu)化問(wèn)題[6-8]。本文采用遺傳算法，根據(jù)運(yùn)輸問(wèn)題的資源分配特點(diǎn)進(jìn)行求解[9]。編組站配流和調(diào)機(jī)運(yùn)用協(xié)調(diào)決策問(wèn)題有其特殊性，需設(shè)計(jì)有效的編碼及適應(yīng)函數(shù)。

4.1 編碼及適應(yīng)值函數(shù)

遺傳算法編碼方法靈活，且無(wú)規(guī)范的方法，在應(yīng)用遺傳算法求解車(chē)列解編排序問(wèn)題時(shí)，由于問(wèn)題所固有的特殊性，采用傳統(tǒng)的二進(jìn)制方式表示解空間，不僅復(fù)雜而且不便于處理不可行解的操作，最方便的編碼方式是直接利用列車(chē)解編順序作為基因。設(shè)J 為到達(dá)列車(chē)解體順序方案，B 為出發(fā)列車(chē)編組順序方案。設(shè)J 、B 對(duì)應(yīng)的調(diào)機(jī)特征向量P={p1,p2,…,pu,…,pv}，pu表示解體（或編組）列車(chē)ddu（或cfu）的調(diào)機(jī)編號(hào)，v 為解體或編組列車(chē)數(shù)。

將調(diào)機(jī)特征向量P 對(duì)應(yīng)的某個(gè)解體或編組順序作為個(gè)體，即任一到達(dá)列車(chē)解體方案J={ddi,dd2,…,ddu,…,ddvJ}，任一出發(fā)列車(chē)編組順序B={cfi,cf2,…,cfu,…,cfvB}。顯然，J 、B 分別為到達(dá)列車(chē)或出發(fā)列車(chē)編號(hào)的一個(gè)排列。由于列車(chē)解編順序的遺傳編碼并不能將約束條件表示出來(lái)，因此為了獲得可行的解體順序初始群體，可依據(jù)解體序號(hào)矩陣進(jìn)行有效編碼，限制不可行解的產(chǎn)生，具體的編碼過(guò)程可參考文獻(xiàn)[10]。

對(duì)任一解體方案J 和編組方案B 配流時(shí)，可根據(jù)式（15）計(jì)算配流方案中欠軸列車(chē)的列數(shù)，因此可將目標(biāo)函數(shù)作為適應(yīng)值函數(shù)。由此，適應(yīng)函數(shù)可取：

4.2 算法思路

初始時(shí)，出發(fā)列車(chē)以先發(fā)先編的原則進(jìn)行排序，到達(dá)解體列車(chē)根據(jù)解體序號(hào)矩陣隨機(jī)產(chǎn)生若干個(gè)v 階解體順序排列作為初始群體，采用聯(lián)賽選擇規(guī)則對(duì)初始種群進(jìn)行篩選，找出若干優(yōu)化解。交叉規(guī)則采用非常規(guī)碼常規(guī)交配法，變異規(guī)則采用交換變異算子，從解體序號(hào)矩陣限制的列車(chē)序號(hào)中隨機(jī)選擇兩個(gè)變異點(diǎn)，按一定的概率進(jìn)行變異，互相交換兩個(gè)基因位置。對(duì)新個(gè)體重新按適應(yīng)值進(jìn)行排序，排在最后的染色體性能最差，將其用上一代最優(yōu)染色體代替。在利用傳統(tǒng)遺傳算法時(shí)，交叉概率pc和變異概率pm在迭代過(guò)程中始終不變。在求解本模型時(shí)，可取pc和pm隨著適應(yīng)度動(dòng)態(tài)變化，如此當(dāng)種群各個(gè)體適應(yīng)度趨于一致或趨于最優(yōu)解時(shí)，pc和pm增大；當(dāng)群體適應(yīng)度比較分散時(shí)，pc和pm減小。由歷史最優(yōu)解體方案，對(duì)出發(fā)列車(chē)依次進(jìn)行配流，并根據(jù)當(dāng)前配流方案安排解編調(diào)機(jī)；若出發(fā)列車(chē)均滿(mǎn)軸，則輸出配流方案及調(diào)機(jī)安排，否則根據(jù)文獻(xiàn)[11]的方法調(diào)整編組順序，重新構(gòu)造解體序號(hào)矩陣。最后以確定迭代代數(shù)作為停止準(zhǔn)則。算法步驟如下：

步驟1初始化遺傳算法相關(guān)參數(shù)。

步驟2以先發(fā)先編的原則進(jìn)行的出發(fā)列車(chē)排序?yàn)槌跏紬l件，構(gòu)造解體序號(hào)矩陣。

步驟3根據(jù)解體序號(hào)矩陣隨機(jī)產(chǎn)生若干個(gè)v 階解體順序排列作為初始群體。

步驟4采用聯(lián)賽選擇規(guī)則對(duì)群體進(jìn)行篩選，找出若干優(yōu)化解。

步驟5根據(jù)優(yōu)化群體對(duì)出發(fā)列車(chē)進(jìn)行配流，分別計(jì)算適應(yīng)度函數(shù)值，記錄最優(yōu)解體順序，并安排解體調(diào)機(jī)。

步驟6若出發(fā)列車(chē)均滿(mǎn)軸，則轉(zhuǎn)步驟7，否則進(jìn)行交叉和變異操作，重新計(jì)算適應(yīng)度函數(shù)值，記錄本次迭代最優(yōu)解，將其與歷史最優(yōu)解做比較，若優(yōu)于歷史最優(yōu)解，則用其替換歷史最優(yōu)解，否則轉(zhuǎn)步驟4。

步驟7按照設(shè)定的條件，判斷迭代是否終止，若終止，則輸出歷史最優(yōu)解，否則轉(zhuǎn)步驟5。

步驟8重新檢查出發(fā)列車(chē)是否均滿(mǎn)軸，若滿(mǎn)軸，則安排編組調(diào)機(jī)，同時(shí)輸出配流方案及解編調(diào)機(jī)安排，否則調(diào)整編組順序，重新構(gòu)造解體序號(hào)矩陣，轉(zhuǎn)步驟3。

編組站的車(chē)流組織工作具有時(shí)變性的特征，雖然有很多算法可以得出模型的解，但是花費(fèi)時(shí)間資源太多，這不符合動(dòng)態(tài)調(diào)度的要求。動(dòng)態(tài)調(diào)度要求優(yōu)化解必須在一定時(shí)間內(nèi)得到，即使所得解不一定最優(yōu)，次優(yōu)也可以接受。解體序號(hào)矩陣的構(gòu)造方法從車(chē)流接續(xù)時(shí)間上保證了遺傳算法以此產(chǎn)生的初始群體都為可行解，且變異操作也在解體序號(hào)矩陣限制的列車(chē)序號(hào)中選擇，避免了不可行個(gè)體的產(chǎn)生。交叉和變異概率的動(dòng)態(tài)變化，使個(gè)體產(chǎn)生的配流方案逐步接近全部滿(mǎn)軸。因此，由解體序號(hào)矩陣產(chǎn)生的群體保證了算法的收斂性。

5 算例

5.1 時(shí)間標(biāo)準(zhǔn)及到發(fā)車(chē)流數(shù)據(jù)

某編組站列車(chē)解體、編組由不同的調(diào)機(jī)擔(dān)當(dāng)，解體、編組調(diào)機(jī)均為2 臺(tái)。列車(chē)到達(dá)作業(yè)時(shí)間標(biāo)準(zhǔn)為35 min，出發(fā)作業(yè)時(shí)間標(biāo)準(zhǔn)為25 min，列車(chē)解體時(shí)間標(biāo)準(zhǔn)為25 min，編組作業(yè)時(shí)間標(biāo)準(zhǔn)為25 min。選取其中一個(gè)階段的到發(fā)原始車(chē)流數(shù)據(jù)，見(jiàn)表1 和表2（其中10000 為調(diào)車(chē)場(chǎng)現(xiàn)車(chē)）。

表1 到達(dá)列車(chē)車(chē)流

表2 出發(fā)列車(chē)車(chē)流

5.2 算法結(jié)果分析

根據(jù)編組站配流問(wèn)題的特點(diǎn)所改進(jìn)的遺傳算法，采用了增強(qiáng)型的初始種群生產(chǎn)策略，利用解體序號(hào)矩陣限制不可行解的產(chǎn)生，減少了遺傳算法本身隨機(jī)性帶來(lái)的影響，并通過(guò)有限制的個(gè)體變異操作，避免了變異操作的盲目性，使變異后的種群能向高適應(yīng)度方向進(jìn)化，在每次變異后對(duì)母子染色體的適應(yīng)度進(jìn)行比較，只保留適應(yīng)度高的個(gè)體，從而增強(qiáng)了種群適應(yīng)度，使算法能夠沿著出發(fā)列車(chē)全部滿(mǎn)軸的方向前進(jìn)，最終達(dá)到種群適應(yīng)度高、運(yùn)行代數(shù)和運(yùn)行時(shí)間少的效果。

在求解配流方案時(shí)，在遺傳算法中設(shè)定種群規(guī)模popsize=50，初始交叉率pc=0.8，變異率pm=0.08，最大進(jìn)化代數(shù)根據(jù)實(shí)例不同設(shè)定為50～100 代不等。算法采用VC++6.0 語(yǔ)言編程，在LENOVO 酷睿TM2 計(jì)算機(jī)上，經(jīng)過(guò)多次測(cè)算，結(jié)果表明采用遺傳算法一般能在30 s 內(nèi)收斂到最優(yōu)解（或滿(mǎn)意解），其中一次以配流方案中欠軸列車(chē)數(shù)最少為目標(biāo)運(yùn)行得到的配流方案和調(diào)機(jī)運(yùn)用方案如表3、表4和表5 所示。將表2 和表3 對(duì)比可以看出，出發(fā)列車(chē)均已滿(mǎn)軸。從表4 和表5 的解編調(diào)機(jī)安排分析可知，到達(dá)列車(chē)的平均待解時(shí)間為36.4 min，出發(fā)列車(chē)的平均待發(fā)時(shí)間為41.5 min，若在保證列車(chē)均滿(mǎn)軸的前提下以待解和待發(fā)時(shí)間最小為目標(biāo)，列車(chē)的配流方案還有進(jìn)一步優(yōu)化的空間。

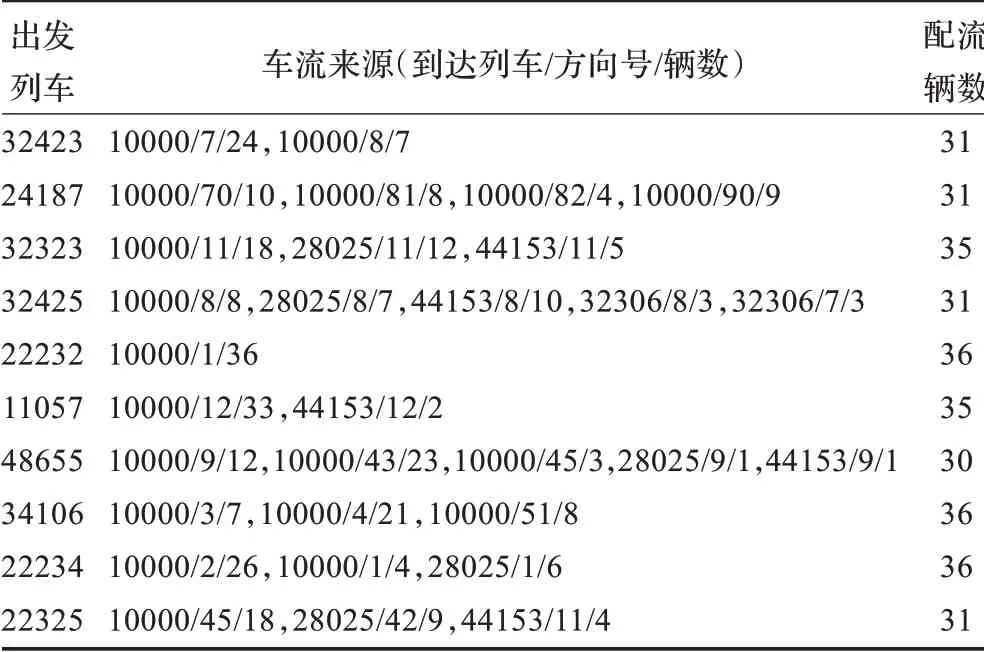
表3 最終配流方案

表4 解體調(diào)機(jī)安排

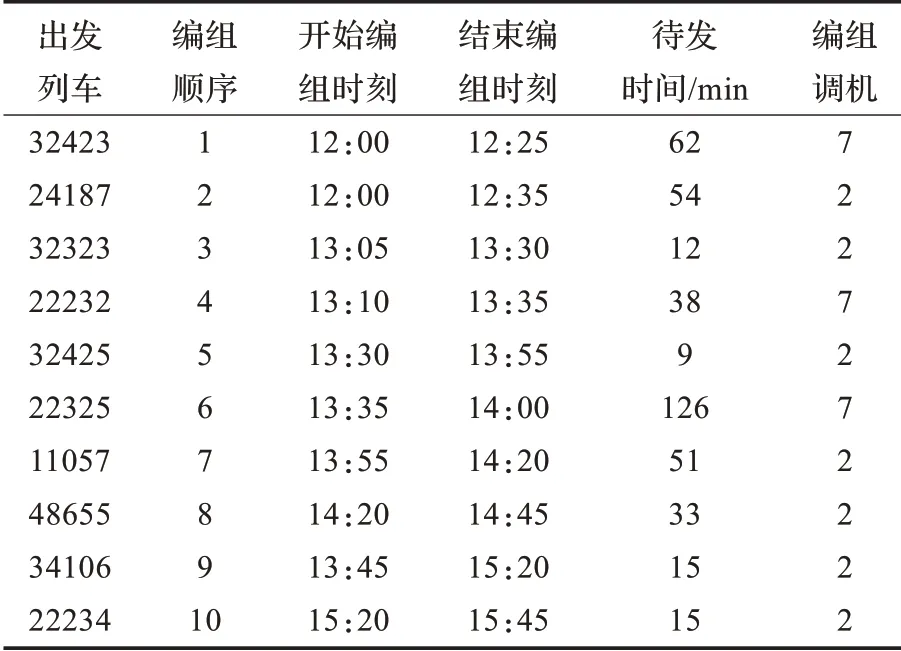
表5 編組調(diào)機(jī)安排

6 結(jié)論

本文構(gòu)建的基于列車(chē)配流和調(diào)機(jī)運(yùn)用約束的協(xié)調(diào)決策優(yōu)化模型，能夠較好地描述編組站站配流和調(diào)機(jī)運(yùn)用的協(xié)調(diào)問(wèn)題。針對(duì)該問(wèn)題，采用增強(qiáng)型的初始種群生產(chǎn)策略，利用解體序號(hào)矩陣限制不可行解的產(chǎn)生，并通過(guò)有限制的個(gè)體變異操作，使變異后的種群向高適應(yīng)度方向進(jìn)化。通過(guò)實(shí)例驗(yàn)算，表明采用遺傳算法能夠快速求解出滿(mǎn)意的配流方案。在編組站實(shí)際工作中，列車(chē)預(yù)計(jì)的到達(dá)和出發(fā)時(shí)間與實(shí)際的到達(dá)、出發(fā)時(shí)間會(huì)有出入，需要通過(guò)人機(jī)對(duì)話(huà)動(dòng)態(tài)調(diào)整，以保證系統(tǒng)運(yùn)算結(jié)果的實(shí)用性。

[1] 王明慧，趙強(qiáng).編組站智能調(diào)度系統(tǒng)階段計(jì)劃優(yōu)化模型及算法研究[J].鐵道學(xué)報(bào)，2005，27（6）：1-9.

[2] 李文權(quán).鐵路區(qū)段站日工作計(jì)劃優(yōu)化模型及其算法的研究[D].成都：西南交通大學(xué)，1997.

[3] 王正彬.區(qū)段站階段計(jì)劃調(diào)整模型與算法研究[D].成都：西南交通大學(xué)，2007.

[4] 王慈光.運(yùn)輸模型及優(yōu)化[M].北京：中國(guó)鐵道出版社，2004.

[5] 薛鋒，羅建，陳崇雙.編組站配流中解編時(shí)刻參數(shù)的計(jì)算[J].交通運(yùn)輸工程與信息學(xué)報(bào)，2010，8（4）：21-27.

[6] 牛惠民，胡安洲.雙向編組站車(chē)流接續(xù)的綜合優(yōu)化[J].鐵道學(xué)報(bào)，1998，20（6）：16-21.

[7] 崔炳謀，馬鈞培，張樸.編組站進(jìn)路調(diào)度優(yōu)化算法[J].中國(guó)鐵道科學(xué)，2007，28（2）：100-103.

[8] 劉霆，何世偉，王保華，等.編組站調(diào)度計(jì)劃隨機(jī)機(jī)會(huì)約束規(guī)劃模型及算法研究[J].鐵道學(xué)報(bào)，2007，29（4）：12-17.

[9] 薛鋒，羅建.基于遺傳算法的動(dòng)態(tài)MC2 運(yùn)輸問(wèn)題求解[J].計(jì)算機(jī)工程與應(yīng)用，2008，44（28）：236-238.

[10] 薛鋒，王慈光，張展杰.編組站配流的協(xié)調(diào)優(yōu)化算法[J].西南交通大學(xué)學(xué)報(bào)，2010，45（6）：932-937.

[11] 薛鋒，王慈光.編組站列車(chē)編組順序的調(diào)整方法[J].鐵道學(xué)報(bào)，2007，29（4）：1-5.