軟分離性的進一步研究

張雄偉

陜西榆林學院 數學與應用系，陜西 榆林 719000

現實世界是復雜以至于人們不能及時、直接地理解，于是人們創造了實際的“模型”，對現實世界的某些方面進行簡化。于是在1999年，Molodtsov D在文獻[1]介紹了軟集的概念，開始發展一種新的方法作為研究不確定性模型的理論。最近，Shabir和Naz在文獻[2]中提出了軟開集、軟閉集、軟閉包、軟內點、點的軟鄰域和軟分離公理，并介紹了它們的基本性質，對軟拓撲空間上軟Ti(i=1,2,3,4)，軟正規空間和軟正則空間作了詳細闡述。在文獻[3]，Min W K指出了文獻[2]中的注4是錯誤的，并且給出了具體的例子闡述這一問題，基于文獻[2-3]，本文提出了軟Urysohn空間和軟T5空間的概念，給文獻[2]中的注4提供一個正確的例子，研究了諸軟分離公理之間的關系。

1 預備知識

下面給出一些關于軟集的有關知識。

定義1.1[1]X上的一個軟集是一個偶對（這里E是一個非空參數集），且M:E→2X是一個映射，X上的軟集的全體記為：(2X)E。

定義1.2[2]每一個 A∈2X，定義 (?,E)∈(2X)E如下(i)=A?(?e∈ E)；把和?認為是一樣的 ?(?x∈X)。每一個 (M,E)∈(2X)E,定 義 (M′,E)∈(2X)E如 下 ：M′(e)=XM(e)?(?e∈ E) ；有 時 使 用 (M,E)′（resp.?）代 替 (M′,E)（resp.(?,E)）。

定義1.3[2]設 X是一個集合，T?(2X)E。(X,T,E)稱為X的一個軟拓撲空間，若T對任意并運算和有限非空交元算關閉，T稱為X的一個軟拓撲，T中的成員稱為軟開集，對每一個(M,E)∈T,(M′,E)稱為一個軟閉集。={(M,E)?(N,E(N,E)∈T′}，明顯地對每一個 e∈E ，集族Te={M(e)|(M,E)∈T}是 X上的一個拓撲。對每一個(M,E)∈(2X)E，有 (ˉ,E。這里(e)=，對每一個e∈E，指 M(e)在 Te中的閉包。

定理1.1[3]（1）設(X,T,E)是一個 X上的軟拓撲空間。若 (X,T,E)是一個軟T3空間，則對每一個 x∈X,(x?,E)是軟閉的。

（2）軟T3空間是軟T2空間。

在下文，若沒有提到和解釋的概念，有關軟拓撲空間的一些概念和性質可以在文獻[2]中找到。

2 軟Urysohn空間和軟T5空間

本章先給出軟Urysohn空間和軟T5空間的概念。

定義2.1設(X,T,E)是X上的軟拓撲空間，?x,y∈X且 x≠y，若存在軟開集(M,E)和(N,E)使得 x∈(M,E),y∈(N,E)(X,T,E)稱為是一個軟Urysohn空間。

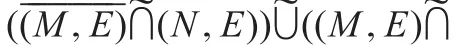
定義2.2設(X,T,E)是X上的軟拓撲空間，?(M,E),(N,E,X)∈(2X)E滿足下面條件：，若存在軟開集 (P,E,X)和 (Q,E,X)使得T,E)稱為是一個軟完全正規空間。(X,T,E)稱為是一個軟T5空間，若它是一個軟完全正規空間且是一個軟T1空間。

本章的主要結果如下：

定理2.1設(X,T,E)是一個軟拓撲空間。

（1）若(X,T,E)是一個軟T5空間，則(X,T,E)是一個軟T4空間。

（2）若 (X,T,E)是一個軟Urysohn空間，則 (X,Te)是一個Urysohn空間 ?(?e∈ E)。

（3）若(X,T,E)是一個軟Urysohn空間且Y是 X上的一個非空子集，則(X,TY,E)是一個軟Urysohn空間。

（2）?x,y∈Y且 x=y，由于(X,T,E)是一個軟Urysohn空間，存在軟開集(M,E)∈T和(N,E)∈T使得 x∈(M,E),一個Urysohn空間 (?e∈E)。（3）?x,y∈Y 且 x=y，則存在軟開集 (M,E)∈T 和是一個Y上的軟閉集，記(MY,E)和所以(X,TY,E)是一個軟Urysohn空間。

定理2.2（1）若(X,T,E)是一個軟T3空間，則(X,T,E)是一個軟Urysohn空間。

（2）若 (X,T,E)是一個軟Urysohn空間，則 (X,T,E)是一個軟T2空間。

證明（1）設(X,T,E)是一個軟T3空間。首先，對每一個 x∈X和每一個開軟集(M,E)滿足 x∈(M,E)，存在開軟集(N,E)滿足 x∈(N,E)使得。事實上，設 x∈X 和 (F,E)∈T 滿足 x∈(F,E)，則 x∈(F,E)′∈T′，因此(X,T,E)是一個軟T3空間，存在軟集(M,E)和(N,E)滿足 x∈(M,E)和其次，由定理2.1可知(X,T,E)是軟T2空間，設 x≠y，則存在軟開集(M,E)和 (N,E)滿足 x∈(M,E)和 y∈(N,E)使得因此，存在開軟集 (P,E)滿足 x∈(P,E)使得且存在開軟集 (Q,E)滿足 y∈，因此(X,T,E)是一個軟Urysohn空間。

（2）容易證明，略。

注1（1）若(X,T,E)是一個軟正規空間，則(X,T,E)不一定是一個軟正則空間。

（2）若(X,T,E)是一個軟正規空間，且Y是 X的一個非空子集，則(X,TY,E)不一定是一個軟正規空間。事實上，設 (Y,TY,E)不是一個軟正規空間，∞?Y，設 X=可以證明(X,T,E)是一個軟拓(F,E,X)和 (G,E,X)是 X上的軟閉集滿足(G,E,X)=?，則其中之一不含∞，不妨設為(F,E,X)，所以 (F′,E,X)=?，因此 (F,E,X)=?，則存在軟開集 ??和T,E)是一個軟正規空間。

（3）文獻[2]中注5①一個軟T4空間不一定是軟T3空間。

②若(X,T,E)是一個軟T4空間，則對每一個e∈E，(X,Te)不一定是T4空間。

③若(X,T,E)是一個軟T4空間，且Y是 X的一個非空子集，則(X,TY,E)不一定是一個軟T4空間。

可以證明文獻[2]中注5的陳述是正確的，但是它的例子是不正確的，即文獻[2]中例10是不正確的。因為存在軟開集?滿足 h4∈?，但 hi∈=1,2,3)，因此 (X,T,E)不是一個軟T1空間，所以(X,T,E)不是一個軟T4空間。

下面給出正確的例子：

例2.1設X={1 ,2,3,4},E={e1,e2},T={?,?,(F1,E),(F2,E),…,(F22,E)},這里的

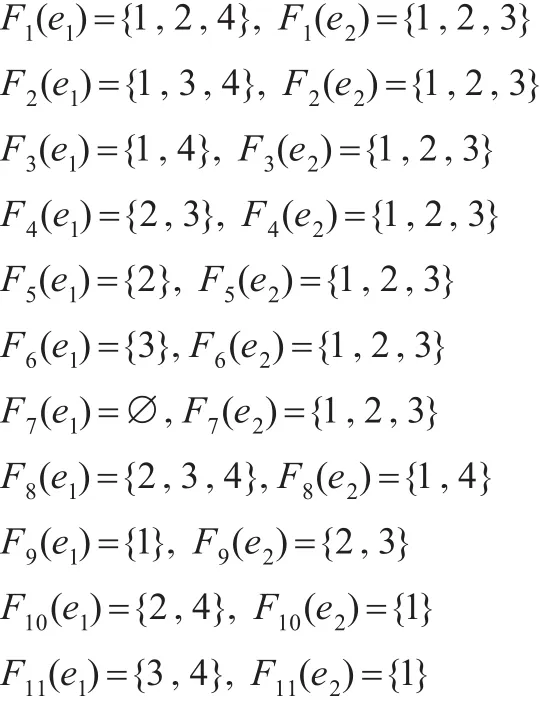
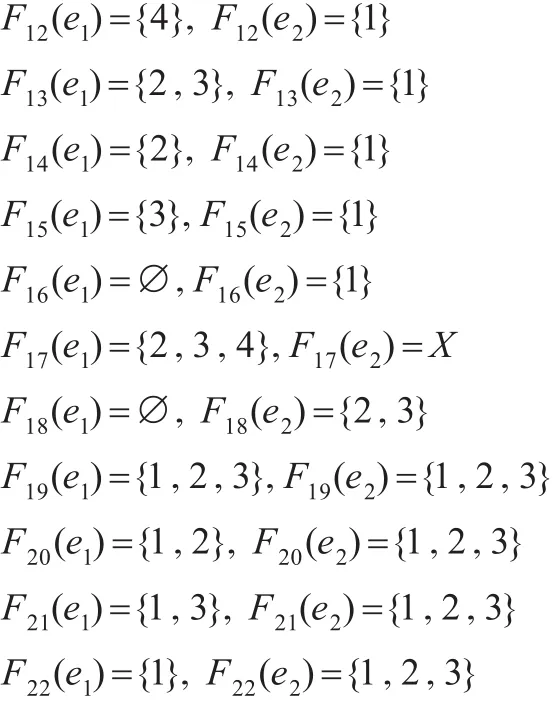
則可以證明(X,T,E)是軟正規空間且是軟T1空間。即(X,T,E)是一個軟T4空間，但不是T3空間，因為1∈?和(F3,E)′是 X的一個軟集滿足1?(F3,E)′，所有軟開集(Fi,E)?(i=1,2,3,19,20,21,22) 和滿 足 1∈(Fi,E) 和1∈?, 所 有 軟 開 集 (Fj,E)?(j=8,17) 和?滿 足，即不存在軟開集 (F,E)和(G,E)滿足,因此每一個軟T4空間不必是一個軟T3空間。

現在由于 Te2={?,X,{1,2,3},{1,4},{2,3},{1}}，因為2≠3，所有的開集{2,3},{1,2,3}和 X滿足 2∈{2,3},2∈{1,2,3}且2∈X也包含元素3，所以(X,Te2)不一定是一個T1空間，因此(X,Te2)不一定是一個T4空間。

取 Y={1,2,3},則 TY={?,?(FY1,E),(FY2,E),…,(F12,E)}。這里的

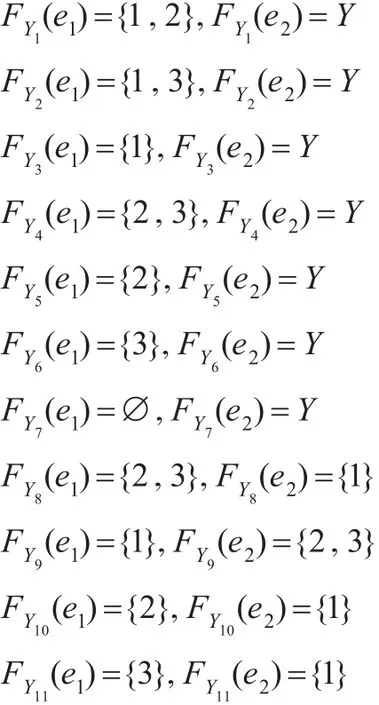
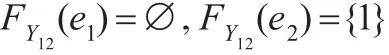
則容易證明(X,T,E)是一個軟T1空間，但不一定是一個軟正規空間，因為(FY2,E)′和(FY5,E)′是Y上的兩個軟閉集，使得所有軟開集 (FYi,E)(i=1,4,5,8,10)和?滿足i和和存在軟開集 (FY,E)和?滿足2和但是,即不存在 Y 上的軟開集 (F,E)和 (G,E)滿足(F,E)和使得因此一個軟T4的子空間不一定是軟T4空間。

3 軟分離性的各種關系

在本章，作為本文的結束，將給出幾種分離關系如下：

定理3.1 T5?T4?T3? 軟Urysohn空間?T2?T1?T0；T5?軟完全正規空間?軟正規空間?軟正則空間。

證明由定理1.1、定理2.1～2.2、注2.1以及文獻[2]，易知定理3.1是成立的。

[1]Molodtsov D.Soft set theory-first results[J].Computers and Mathematics with Applications，1999，37（4/5）：19-31.

[2]Shabir M，Naz M.On soft topological spaces[J].Computers and Mathematics with Applications，2011，61：1786-1799.

[3]Min W K.A note on soft topological spaces[J].Computers and Mathematics with Applications，2011，62：3524-3528.

[4]Cagman N，Karatas S，Enginoglu S.Soft topology[J].Computers and Mathematics with Applications，2011，62（1）：351-358.

[5]Sezgin A，Atagün A O.Soft groups and normalistic soft groups[J].Computers and Mathematics with Applications，2011，62（2）：685-698.

[6]Tanay B，Kandemir M B.Topological structure of fuzzy soft sets[J].Computers and Mathematics with Applications，2011，61：2952-2957.

[7]Aygünolu A，Aygün H.Introduction to fuzzy soft groups[J].Computers and Mathematics with Applications，2009，58（6）：1279-1286.

[8]Jun Y B，Lee K J，Zhan J M.Soft p-ideals of soft BCI-algebras[J].Computers and Mathematics with Applications，2009，58（10）：2060-2068.

[9]Yang C F.Fuzzy soft semigroups and fuzzy soft ideals[J].Computers and Mathematics with Applications，2011，61（2）：255-261.