“補償法”在普通物理教學中的應用

趙 強 韓春杰

(石家莊機械化步兵學院 河北 石家莊 050083)

大學物理中所學的定理、定律或公式通常是解決具有對稱性分布的物理問題，而在解題過程中，常常遇到某些物理量分布不對稱性的問題.如何利用已有的知識解決這些難題，是學生深感困惑的事情.利用補償法巧妙地將一些不對稱分布問題假設在一定條件下變為對稱分布，從而，使原問題的求解過程簡化或通過補償消除某些非對稱因素，將復雜的物理問題由難變易，由繁變簡.在計算挖空物體的轉動慣量、帶電體的電場強度和載流導體的磁感應強度等問題時常常用到補償法求解.

1 求剛體的轉動慣量

解析：本題如根據轉動慣量的定義積分計算比較困難.但用“補償法”(或稱“負質量法”)計算，就簡單得多.設想在帶孔圓盤的每個小孔處填充質量為正的和負的且相等的小圓盤, 這樣，并不改變原來的質量分布[2], 但形成了正質量的大圓盤和兩個負質量的小圓盤的組合體, 它們的轉動慣量都可按公式計算, 帶孔圓盤的轉動慣量即可求得.

正質量的大圓盤對盤心O軸的轉動慣量為

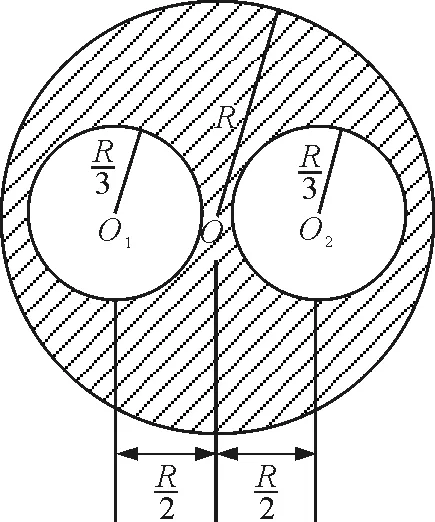
圖1

兩個負質量的小圓盤對O軸的轉動慣量為

所以帶孔圓盤對O軸的轉動慣量為

2 求解帶電體的電場強度

【例2】如圖2所示，在電荷體密度為ρ的均勻帶電球體中，存在一個球形空腔，若將帶電體球心O指向空腔球心O′的矢量用a表示，試求球形空腔中任一點的電場強度[3].

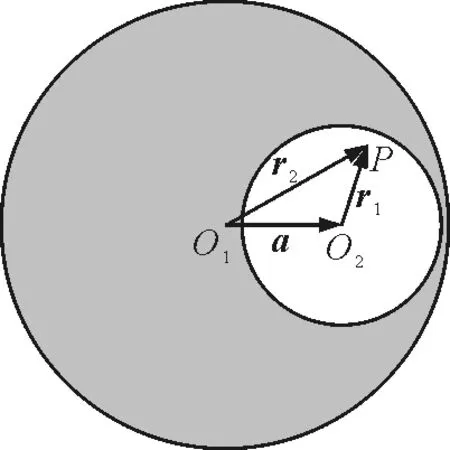
圖2

解析：本題所給的帶電體的電荷分布不滿足球對稱，它的電場分布也不是球對稱分布，因此,無法用高斯定理求其電場分布，也無法用點電荷場強公式由積分法求得，但可用場強的疊加原理，即補償法進行求解.具體方法是挖去空腔球體的電場強度加上補有同樣電荷體密度的空腔球體的電場強度，就等于整個球體的電場強度.由于整個球體和補有電荷的空腔球體的電場強度很容易求出，所以,挖去空腔球體的電場強度就可以求出.

挖去空腔的帶電球體在電學上等效于一個完整的、電荷體密度為ρ的均勻帶電球體和一個電荷體密度為-ρ的空腔球體.這樣，利用電場強度的疊加原理，挖去空腔的帶電球體的電場強度就可以計算.

均勻帶電球體內部一點的電場強度，由高斯定理可得

由幾何關系可得

r1-r2=a

所以

3 求載流導體的磁場分布

【例3】如圖3所示，一根半徑為R的無限長載流直導體，在導體上有一半徑為R′的圓柱形空腔，該空腔的軸與直導體的軸平行，兩軸相距為d(d>R′).導體中有電流I沿軸向流過，并均勻分布在橫截面上.試求空心部分軸線上的磁感應強度的大小[4].

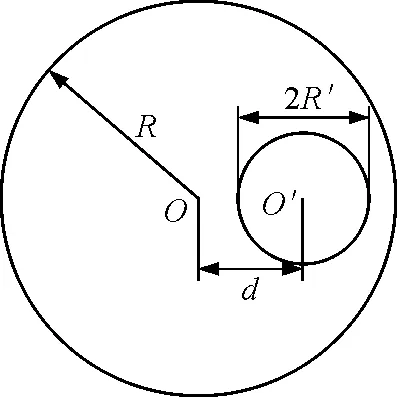
圖3

解析：題中給出的電流為非對稱分布，產生的磁場分布不具有軸對稱性，因而不能用安培環路定理直接求解.但可以利用補償法求空腔內的磁場分布.將題中的載流導體視作兩個半徑分別為R和R′的實心圓柱形導體，其電流密度j均為

但兩導體上電流的流向相反.這相當于在原導體空腔處補上電流密度相同、電流方向相反的兩束電流，此時空腔內任一點的磁感強度為B=B1+B2.

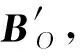
由安培環路定理知，空心圓柱體在其軸心處的磁感應強度

實心圓柱體在O′處的磁感應強度可由安培環路定理求出

所以

參考文獻

1 康穎．大學物理(下冊)．北京：科學出版社，2006.152

2 程國均．大學物理學教程．北京：科學出版社，2002.156

3 馬文蔚．物理學(中冊)．北京：高等教育出版社，2002.53

4 張三慧．大學物理學(第三冊)．北京：清華大學出版社，2000.180