裝備更新經(jīng)濟性分析

張麗葉， 邢 偉

（1.裝備學院 裝備采辦系，北京101416； 2.裝備學院 學院辦公室，北京101416）

裝備隨著使用年限的增加，其故障逐年增多，維修費用不斷增加，作戰(zhàn)能力降低。如果不能進行適時更新，部隊的戰(zhàn)斗力就不能得到保證，同時也會造成資源的浪費和管理效益的低下［1］。因此，如何選擇更新模式和更新時機日益引起軍方的高度重視。狹義的裝備更新模式包括原型更新和新型更新；廣義的裝備更新模式包括狹義裝備更新、裝備大修以及裝備現(xiàn)代化改裝［2］62－64。裝備更新決策取決于裝備的技術壽命和經(jīng)濟壽命。本文主要從經(jīng)濟分析的角度分析裝備的更新模式和更新時機。文獻［2］62－64介紹了幾種裝備更新的分析方法，如最低費用法、MAPI（Machinery and Allied Products Institute）法、經(jīng)濟壽命法等；文獻［3］闡述了艦艇裝備的磨損和3種壽命，提出了艦艇裝備經(jīng)濟壽命的基本模型。上述文獻并沒有從廣義角度研究裝備更新問題，系統(tǒng)性也不強，建立的更新模型偏重靜態(tài)更新決策模型，沒有實例驗證。本文主要應用技術經(jīng)濟學知識建立動態(tài)的、更加合理的更新決策模型，并進行實例驗證。

1 裝備經(jīng)濟壽命

裝備壽命可分為自然壽命、技術壽命和經(jīng)濟壽命［4］。其中，經(jīng)濟壽命是指從裝備投入使用開始到因繼續(xù)使用不經(jīng)濟而被更新延續(xù)的時間［5］。

1.1 裝備經(jīng)濟壽命計算原理圖

將裝備年度分攤初始投資費和年度平均使用維修費統(tǒng)稱為年度總費用。一方面，裝備的初始投資費是一次確定的，隨著使用年限的增加，年度分攤的初始投資費越來越少；另一方面，裝備隨著使用年限的增加，平均每年用于其使用維修的費用逐年增加［6］。因此，裝備的年度總費用變化規(guī)律是隨著使用時間的延長，呈現(xiàn)先降后升的凹型曲線，并且在某一使用期限，會達到年度總費用的最小值。以上費用變化規(guī)律反映在圖1的3條曲線上。年度總費用最低對應的使用期限就是裝備的經(jīng)濟壽命。

圖1 裝備經(jīng)濟壽命計算原理圖

1.2 裝備經(jīng)濟壽命計算方法

根據(jù)圖1原理，已知裝備初始投資費和裝備在未來使用過程中各年的使用維修費及年末殘值，就可以通過逐年計算年度總費用來求出裝備經(jīng)濟壽命。

n年內(nèi)裝備總費用現(xiàn)值［7］為

則n年內(nèi)裝備年度總費用為

式中：K為裝備初始投資費；Cj為第j年的使用維修費用；Ln為第n年末的殘值；n為使用年限；i為折現(xiàn)率；CPn為費用現(xiàn)值；CAn為年度總費用；（P／F，i，n）為貼現(xiàn)系數(shù)；（A／P，i，n）為等額分付資本回收系數(shù)。根據(jù)經(jīng)濟壽命計算原理，當CAm≤CAm－1，CAm≤CAm＋1時，m年為裝備的經(jīng)濟壽命。

2 裝備更新的決策模型

從經(jīng)濟學角度進行裝備更新決策分析，實質(zhì)上基于裝備經(jīng)濟壽命計算原理和方法構建裝備更新決策模型。裝備更新模式有狹義和廣義2種情況，因此，本文分為2種情況構建裝備更新決策模型。

2.1 裝備狹義更新的決策模型

裝備狹義更新的決策模型分為無新型裝備和有新型裝備條件下的裝備更新模型。

2.1.1 原型更新

有些裝備在整個使用期內(nèi)并不過時，例如彈藥之類的裝備；也有些裝備由于新型號開發(fā)緩慢，長時間都沒法進行新型裝備更新，這種情況在我國比較明顯。這時裝備由于使用中的磨損，使用維修費用不斷增加，采用原型更新在經(jīng)濟上也是相對合算的。對這種情況的決策，可歸結為求原型裝備經(jīng)濟壽命，計算方法同式（2），求得的經(jīng)濟壽命即為原型更新的最佳時期。

2.1.2 新型更新

有些裝備在服役年限內(nèi)還未達到其經(jīng)濟壽命，就出現(xiàn)了新型的裝備，這時需要做出是否更新以及何時更新的決策。這種情況下裝備更新決策依據(jù)是求在特定服役年內(nèi)新舊裝備總費用之和最小對應的年份，即為最佳更新時機。

設裝備服役年限為N年，若第t年末進行更新，則舊裝備使用年限為t年，新型裝備使用年限為N－t年。

舊裝備t年內(nèi)的總費用CPt為

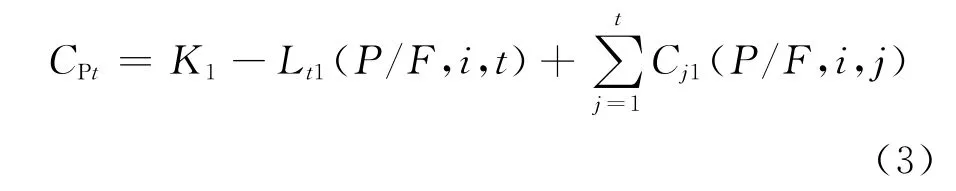
新裝備N－t年的總費用CP（N－t）為

顯然，N年內(nèi)的總費用CPN為

根據(jù)上述公式即可以找出總費用最低的年份，即為最佳更新期。

2.2 裝備廣義更新的決策模型

本文定義：CP為裝備使用到第i年的總費用；K為各種更新方案第i年需要的投資；KL0為舊裝備在第i年的價值；L為裝備使用N年后的殘值；Cj為裝備使用第j年的經(jīng)營費用；β為各種更新方案使用時的勞動生產(chǎn)率系數(shù)。

可以分別計算各種廣義更新方案［8］的年度總費用，按總費用最小的原則進行更新決策，建立的更新模型如式（6）。

3 實例驗證

某型車輛的物理壽命是9a，部隊需要的服務年限也是9a，在此型號投入使用后，如果發(fā)生以下情景時，該如何更新裝備最經(jīng)濟？情景一：如果新型號開發(fā)緩慢，新型號研制周期長達10a之久，那么如何選擇更新方案？情景二：如果新型號開發(fā)順利，5a后就可裝備部隊，新型號可用9a，那么如何選擇更新方案？情景三：如果在服務年限內(nèi)可以進行廣義的更新，那么如何選擇更新方案？假定車輛殘值為零，i0＝7%。

3.1 情景一的更新模式——原型更新

車輛原型更新原始資料，如表1所示。

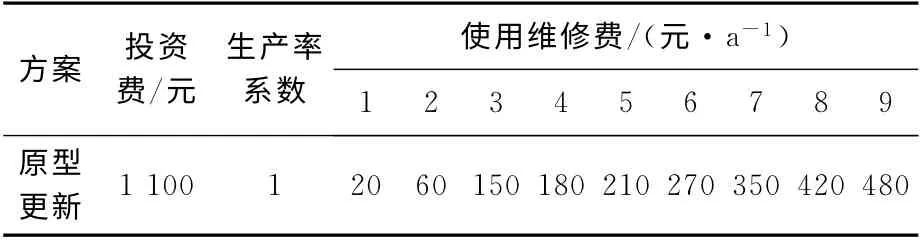
表1 裝備更新方案數(shù)據(jù)資料

對于原型更新模式，只需要將表1數(shù)據(jù)代入式（2），即可求得車輛經(jīng)濟壽命，計算結果見表2。

表2 經(jīng)濟壽命計算結果

從表2可以看出，車輛的經(jīng)濟壽命為7a，即車輛使用7a后進行同型號更新。

3.2 情景二的更新模式——新型更新

車輛新型更新原始資料，如表3所示。車輛已使用5a，服役期還剩4a；舊裝備當前的重置價值為150元／a。

表3 裝備各方案數(shù)據(jù)資料

對于新型更新模式，只需要將表3數(shù)據(jù)代入式（3）～式（5），即可求得車輛更新的時機，計算結果如表4所示。

表4 最優(yōu)更新期計算結果

從表4可以看出，舊型號使用5a后，更新為新型號總費用最低，因此，應當立即更新為新型號。

3.3 情景三的更新模式——廣義更新

車輛廣義更新原始資料如表5所示。舊裝備當前的重置價值為150元／a。

表5 裝備各方案數(shù)據(jù)資料

對于廣義更新模式，只需要將表5數(shù)據(jù)代入式（6），即可計算出各方案逐年費用總額，如表6所示。

表6 各方案費用總額

從表6可以看出，隨著裝備使用年限的不同，裝備更新決策方案也不一樣，具體更新決策結果，如圖2所示。

圖2 車輛更新決策方案

3.4 裝備更新方案決策

情景一——新型號開發(fā)緩慢，新型號研制周期長達10a之久，這時選擇原型更新，更新時間是7a后最經(jīng)濟。

情景二——新型號開發(fā)順利，5a后就可裝備部隊，這時立即進行新型號更新最經(jīng)濟。

情景三——如果在服務年限內(nèi)可以進行廣義的更新，那么可以做如下決策：①如果車輛只考慮使用2a，之后將更新?lián)Q代，此時繼續(xù)使用舊型號的方案為最佳；②如果打算用2～3a，最佳方案是對原裝備進行一次大修；③如果估計裝備將使用3～5a，最佳方案是對原裝備進行現(xiàn)代化改裝；④如果使用5a以上，新型號裝備更新是最佳方案。

4 結 束 語

本文從經(jīng)濟學角度研究了裝備更新問題，得出裝備更新模式和更新時機的選擇依據(jù)和規(guī)律，為裝備更新決策提供思路和方法。實踐中裝備更新方案的選擇還會涉及技術、管理、戰(zhàn)斗力生成等因素，本文僅從經(jīng)濟學角度建立的更新模型將發(fā)生變化。因此，下一步研究還需綜合考慮多種因素的影響，建立裝備更新綜合模型。

（

）

［1］陳鵬，戴鋒，杜劍平.采用動態(tài)規(guī)劃方法合理進行武器裝備更新［J］.軍事運籌與系統(tǒng)工程，2006（1）：54.

［2］呂偉，婁壽春，李同.裝備更新的技術經(jīng)濟分析與探討［J］.戰(zhàn)術導彈技術，2006（3）：62－64.

［3］龔益民，潘艷東，周正.艦艇裝備管理的全壽命周期成本分析［J］.艦船電子工程，2011（6）：153－155.

［4］吳添祖，馮勤，歐陽仲健.技術經(jīng)濟學［M］.北京：清華大學出版社，2004：301.

［5］端木京順.裝備維修技術經(jīng)濟［M］.北京：國防工業(yè)出版社，2003：148.

［6］傅家驥，萬海川.技術經(jīng)濟學概論［M］.北京：高等教育出版社，1992：233.

［7］張金鎖，陳立文.技術經(jīng)濟學原理與方法［M］.北京：機械工業(yè)出版社，2003：84－86.

［8］武春友，張米爾.技術經(jīng)濟學［M］.大連：大連理工大學出版社，2006：244.