基于線陣像機的彈丸速度與姿態測量

回丙偉，趙竹新，文貢堅

（國防科學技術大學ATR重點實驗室，長沙410073）

線陣像機以及傳統的膠片式狹縫攝影機作為一類獨特的光學成像設備，能夠對經過其視平面的目標進行掃描成像，記錄目標在一個極短時間段內的速度和姿態信息，因而在彈丸的攻角測量中具有不可替代的作用[1～5].由于早期的狹縫攝影機參數難以標定，從而無法從攝影幾何的角度建立嚴格的數學成像模型，導致傳統測量方法通常在一定近似條件下進行.這對提高測量的精度極為不利，同時膠片式攝影機復雜的操作過程對靶場測量人員要求較高[2].近年來隨著光電子和計算機技術的發展，一方面線陣像機成像速度越來越高，并以數字化和自動化的突出優點逐步替代膠片式狹縫攝影機；另一方面研究人員對線陣像機的成像模型研究越來越多，線陣像機參數標定技術日趨成熟[6，7]，這為在嚴格線陣像機成像方程下研究目標的運動與姿態參數測量方法奠定了基礎.本文在這種背景下開展了線陣像機靶場測量方法的探索和研究.

為獲得穩定的三維測量結果，測量中常采用交會攝影法獲取多視角圖像.根據線陣像機視場位于一個平面內這一特性，實際中常采用鏡面反射法獲取待測彈丸的立體圖像，如圖1所示.在彈丸飛行軌跡的下方，放置一個大約與水平面成45°的平面鏡，當彈丸從平面鏡上方飛過時，彈丸本身和彈丸在平面鏡中的像都能在該線陣像機中成像.上述方法實現了使用一個線陣像機從2個視角獲取目標立體圖像的目的[8].這種測量方式涉及3個坐標系：①測量坐標系OXYZ，各測量參數均在該坐標系下描述，是測量的基準坐標系；②像機坐標系sxyz，目標特征點的像點坐標在該坐標系下已知，且該坐標系相對于測量坐標系OXYZ的相對方位關系在經過標定后已知；③目標坐標系ox′y′z′，目標上特征點的三維坐標在該坐標系下已知，該坐標系相對于測量坐標系OXYZ的方位關系在本文中是待求參數.下文中，將目標上的一個特征點和其對應的圖像點稱為一對控制點.

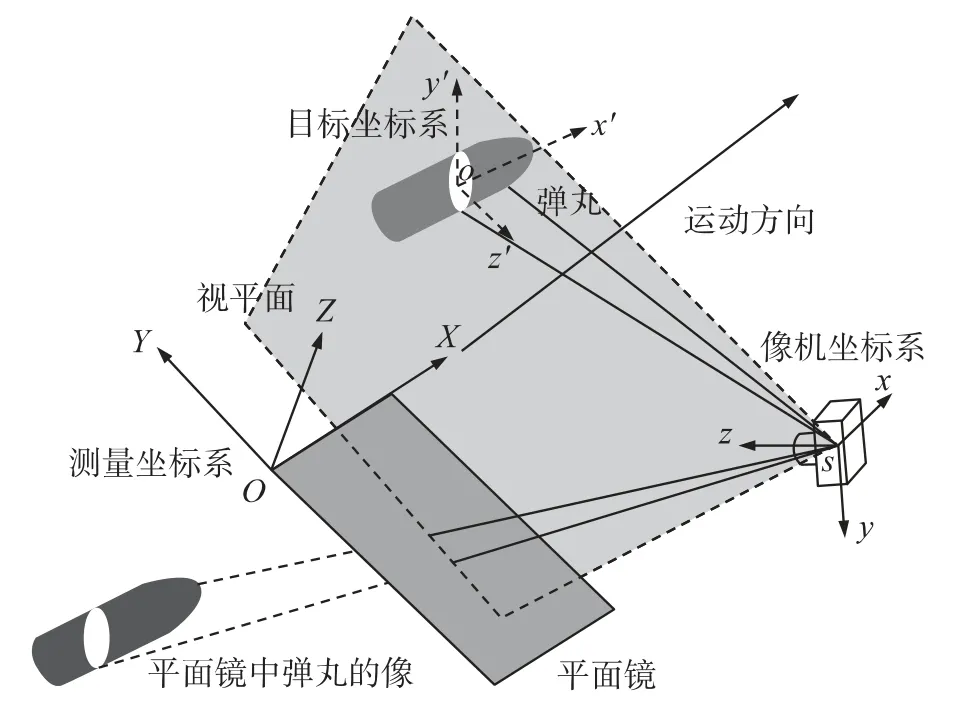
圖1 利用一個線陣像機獲取立體圖像的方法

在攝取到彈丸目標的線陣立體圖像后，基于多對控制點和成像方程，聯立一組以彈丸速度、姿態和初始位置8個參數為未知數的非線性方程組，并進行最優化建模.在對模型求解的過程中，首先利用Powell算法對非線性的姿態參數進行搜索，同時使用線性方程組對位置和速度參數進行求解，并在搜索過程中，對優化模型的目標函數值不斷尋優得到測量初值；然后進一步使用Gauss－Newton法進行精確迭代求解.

1 線陣像機測量原理與成像方程

靜態場景中，線陣像機成像可以看作面陣像機成像的一種特殊情況，只有位于線陣傳感器與主光軸所構成的平面（即視平面[6]）內的場景，能夠按中心投影原理成像.在sxyz中描述，即x≡0，y方向滿足中心投影方程[9]：

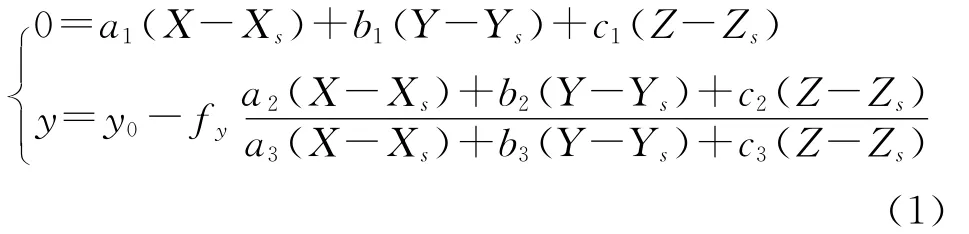
式中，（X，Y，Z）為場景中一點在OXYZ中的空間坐標，y為對應的像點坐標.Xs，Ys，Zs為像機攝影中心在OXYZ中的坐標；旋轉矩陣元素al，bl，cl（l＝1，2，3）是由像機外參數姿態角φ，ω，κ決定的.y0為像主點位置，fy為像機主距，y0、fy統稱為像機內參數.

式（1）的第1式即為視平面的方程，由該式可得：

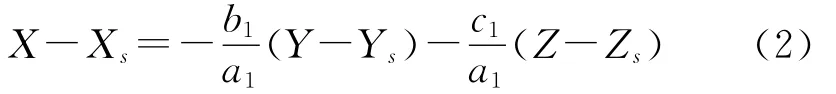
將式（2）代入式（1）中第2式，并根據旋轉矩陣的性質進行化簡，得到線陣像機的靜態成像方程：

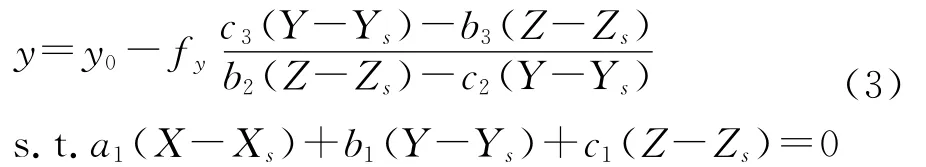
將每一條成像線按時間順次排列成一幅二維圖像，即為線陣像機的動態成像結果，以下稱之為線排列圖像.通常可以認為彈體在經過線陣像機視平面的過程中是保持固定姿態勻速運動的，下面推導該過程中彈體表面點的動態成像方程.

一般三維剛體目標的空間姿態需要用3個空間旋角來表達.由于絕大多數的彈丸目標都具有旋轉體的幾何結構，因此沿彈丸中軸線的自轉角不用考慮，此時其空間姿態通常使用目標繞2個指定坐標軸（本文中即為目標坐標系的y′軸和z′軸）的2個空間旋轉角α和β來描述.并設某一時刻在OXYZ中，目標坐標系原點的坐標為（Xo，Yo，Zo），運動速度矢量v＝（vX vYvZ）；線陣像機的成像頻率為ν；假設目標坐標系中一點（x′，y′，z′）在線陣像機的第n次成像時被捕獲；像機相鄰兩次成像間隔t＝n/ν；并記（DX DY DZ）＝（vX/νvY/νvZ/ν）.可得目標點（x′，y′，z′）在經過線陣像機瞬間的空間坐標（X，Y，Z）為[8]

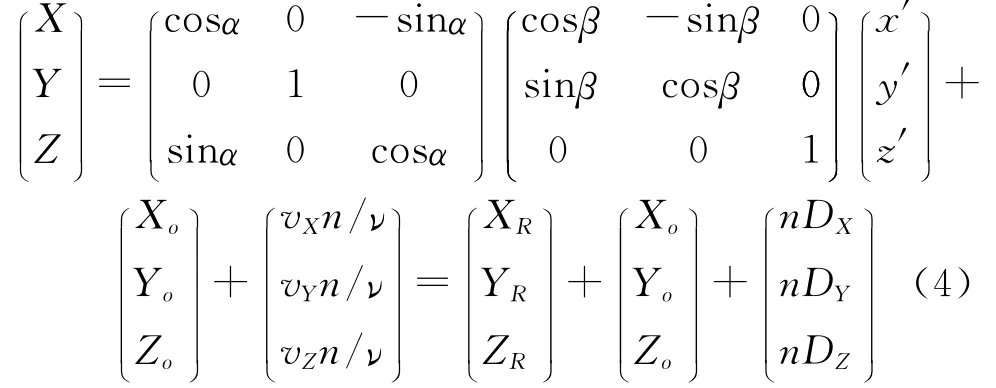
式（4）表明，能在線陣像機中成像的彈丸表面點的空間坐標由三部分確定：彈丸的姿態角α，β決定的（XR，YR，ZR）；初始位置時刻彈丸的目標坐標系原點在OXYZ中的坐標（Xo，Yo，Zo）；彈丸的速度（vX，vY，vZ）決定的（nDX，nDY，nDZ）.因此該式包含了全部待求參數.將式（4）代入式（3），并變換其中的約束條件方程得彈丸目標的動態成像方程：

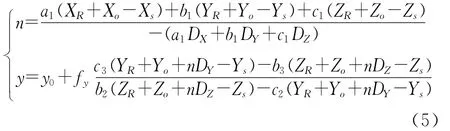
結合平面鏡成像原理，目標點（x′，y′，z′）的鏡像點在OXYZ坐標系中的坐標為

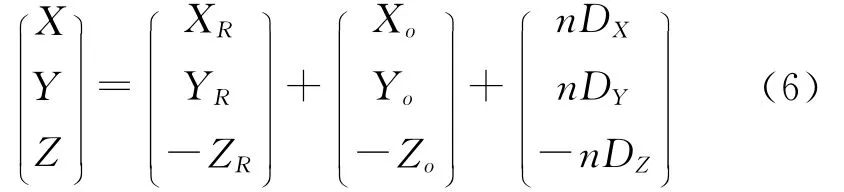
同理將式（6）代入式（3）可得：

因此在上文的假設前提下，式（5）與式（7）分別描述了彈丸目標上任意一點及其平面鏡中的虛像點與各自其圖像點的對應關系.基于這樣一種嚴格幾何成像關系，本文以α，β，DX，DY，DZ，Xo，Yo，Zo為未知量實現彈丸各項參數的測量.

2 速度與姿態測量

2.1 特征點選取與最優化模型

在本文中，彈丸的速度與姿態參數的測量本質上是利用若干對控制點，求解一個含有8個未知數的非線性方程組.由動態成像方程式（5）或式（7）可知，一對控制點可以建立2個方程.因此方程組可解的條件要求至少存在4對控制點.由于彈丸目標在飛行狀態時高速旋轉，其表面的特征點在線排列圖像中通常難以正確識別.而比較穩定的特征點是彈尖和彈尾等特殊點，如圖2所示.

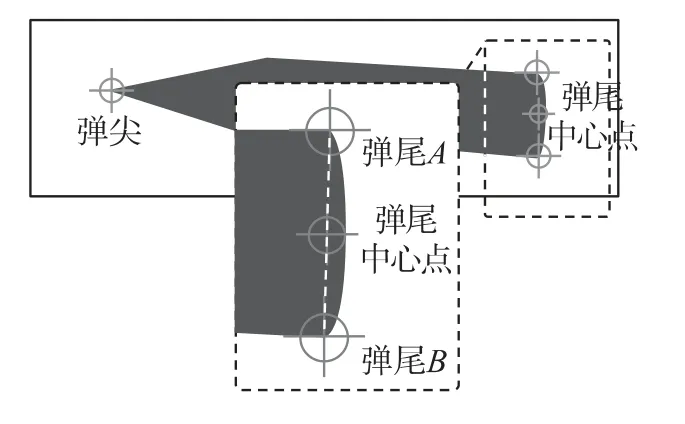
圖2 線排列圖像中彈丸上特殊點的選取

對于彈尖上的控制點，無論在圖像中還是在目標中都是容易確定的；而對于彈尾上來說，圖像上容易識別的上下兩個端點（圖2中的彈尾A和彈尾B）卻在目標坐標系中難以確定，因此本文選擇彈尾的中心點作為控制點，在圖像中表現為A、B兩點連線的中點.這樣從2個視角拍攝的彈丸圖像中可以確定4對控制點，可以滿足方程求解的基本條件.足夠數量的控制點是實現本文測量方法的必要條件.

多元非線性方程組的求解，可根據最小二乘原理轉化為非線性最優化模型來描述.假設目標表面有N個特征點，（i＝1，2，…，N，N≥4），在線陣像機中所成的像點為（ni，yi）.利用（x′i，y′i，z′i），根據一組參數Φ＝（αβDXDYDZXoYoZo），按式（5）或式（7）計算的投影點 坐 標）.若 參 數 向 量Φ能 使（ni，yi）與滿 足 最 優 化 目 標 函 數 時，即 為 方 程 組 的唯一解：

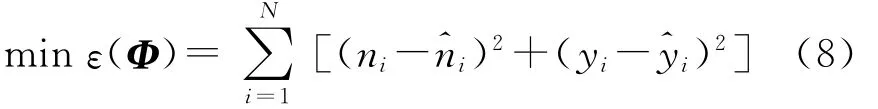
對于式（8）的最優化數學模型，Gauss－Newton法是解決這類問題的經典方法，但對于高維的優化問題，通常需要為其提供一個較好的初值，本節根據模型的特點，利用Powell算法搜索待測參數的近似初始值，然后進一步使用Gauss－Newton迭代法精確求解.

2.2 初值搜索

對于式（5）或式（7）組成的方程，若已知參數α，β，可將其代換為

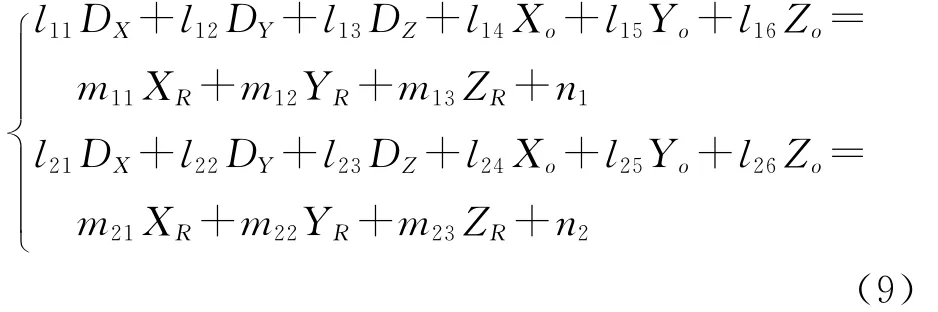
式中，lgh，mgj，ng（g＝1，2；h＝1，2，…，6；j＝1，2，3）均可根據目標上特征點在ox′y′z′中的坐標和像機參數等已知量進行代數換算，（XR，YR，ZR）在給定α，β值的情況也為已知量，因此式（9）是關于6個待求參數DX、DY、DZ、Xo、Yo、Zo的線性方程.利用這一特性和解的唯一性，本文通過對α、β進行搜索，并對每一給定值的α（k）、β（k），利用原方程組解算線性參數，并 尋 找 一 組 參 數在目標函數式（8）的度量下達到最小值，此時可認為其近似為方程組的解.因此，在式（9）的約束下，可認為式（8）的目標函數是關于α、β求極小值的問題.圖3顯示了某次測量中，目標函數值與α、β的關系.為直觀地表現目標函數的極小值，繪圖時對目標函數進行對數變換，這并不影響函數的單調性.

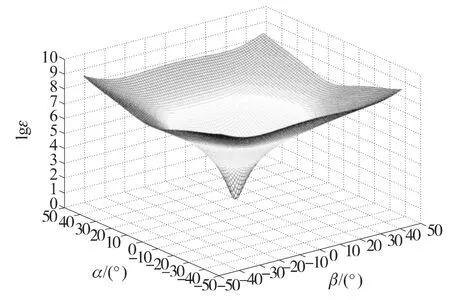
圖3 目標函數值的對數與α、β的關系

下面考慮使用快速的搜索算法使目標函數能在任意α、β初值情況下，快速收斂到極小值，該值即為待測參數的一組近似解.Powell算法是一種不涉及目標函數導數的最優化搜索算法，它是以正定二次函數為背景，以共軛方向為基礎的最優化問題直接搜索方法.該方法具有良好的模塊化特性，已經在許多工程領域獲得了廣泛的應用，本文以Powell算法為基礎搜索方程解的近似值，具體過程如下：

①首先任意設定待求參數初值α（0）、β（0）；

②進入Powell搜索，然后按照算法的搜索規則尋找目標函數極小值，并在第k次搜索中，先將α（k）、β（k）代入式（9），利用線性最小二乘法計算

③將α（k），β（k）代入式（8）計算當前目標函數值ε（k）；

④重復上述步驟②和步驟③直到最終輸出α，β，DX，DY，DZ，Xo，Yo，Zo滿足精度的測量值.

雖然本節Powell搜索中使用的目標函數是按最小二乘的形式定義的，但并不是所有的參數都統一參加了最小二乘平差計算，因此，其搜索結果并不是最小二乘意義下的最優解，下一節將使用嚴格最小二乘迭代求解其精確解.

2.3 迭代求解

根據最小二乘原理，將N個特征點在ox′y′z′中的坐標（x′i，y′i，z′i）視為真值，而 把 相 應 的 圖像點坐標（ni，yi）視為觀測值，對于每一個特征點通過將式（5）或式（7）進行一階泰勒展開，列各點的誤差方程式為

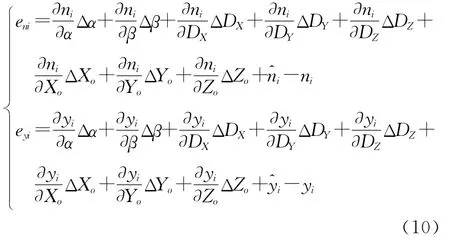
式（10）用矩陣形式表示為

式中，

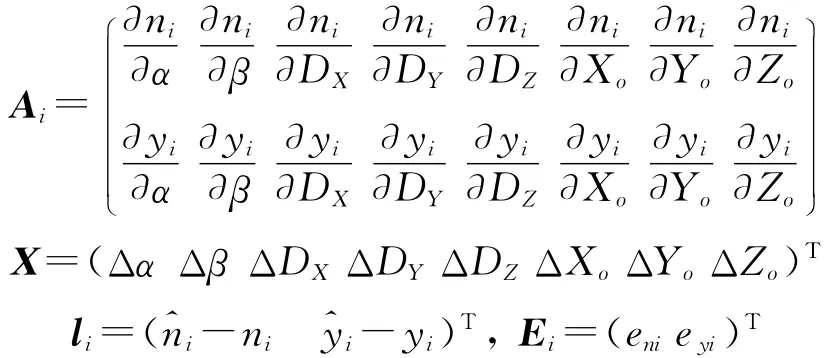
若有N對控制點，則可按式（11）列出N組誤差方程式，共同構成總的誤差方程式：

式中，E＝（E1E2…EN）T，A＝（A1A2…AN）T，L＝（l1l2…lN）T.

根據最小二乘平差原理，可以得到待求參數近似值的改正量：

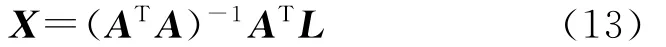
由于式（10）中的各系數取自泰勒級數的線性展開，因此迭代計算通過逐漸趨近的方法，即用原近似值與式（13）求得的改正量的和作為新的近似值，重復上述過程，直至改正量各分量的絕對值小于某一個設定的極限值為止，最后得到待求參數的解.

在得到DX，DY，DZ的精確迭代結果后，彈丸速度（vXvYvZ）＝（νDXνDYνDZ）.

3 仿真實驗

為驗證上述方法的測量精度，本文對不同像機參數下，不同彈丸幾何尺寸和不同的運動姿態參數進行了大量圖像仿真和測量實驗，下文以一組實驗為例進行說明.

首先利用3dMax創建了一個彈長550mm，彈徑70mm的彈丸目標三維表面模型；然后利用第1節線陣像機的成像原理對彈丸飛過像機視場時進行8次仿真成像，每次成像中彈丸運動與姿態參數如表1所示，像機主機像素為fy＝5 000，y0＝0，線陣像機成像速度ν＝140 000s－1.像機外參數如表2所示.

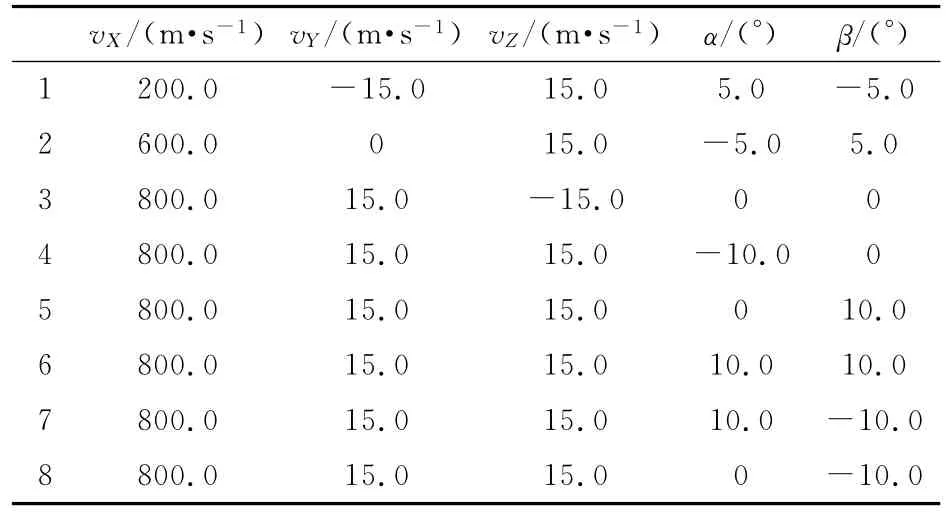
表1 仿真中彈丸目標速度與姿態參數設定值

表2 線陣像機外參數

使用上面第1節與第2節的測量方法，分別對仿真得到的圖像進行測量.對合速度參數v和2個姿態參數分別進行精度比較，如表3所示，表中v為利用表1中的3個速度分量計算所得的合速度的理論值；v′，α′，β′為彈丸合速度與姿態參數的測量值.

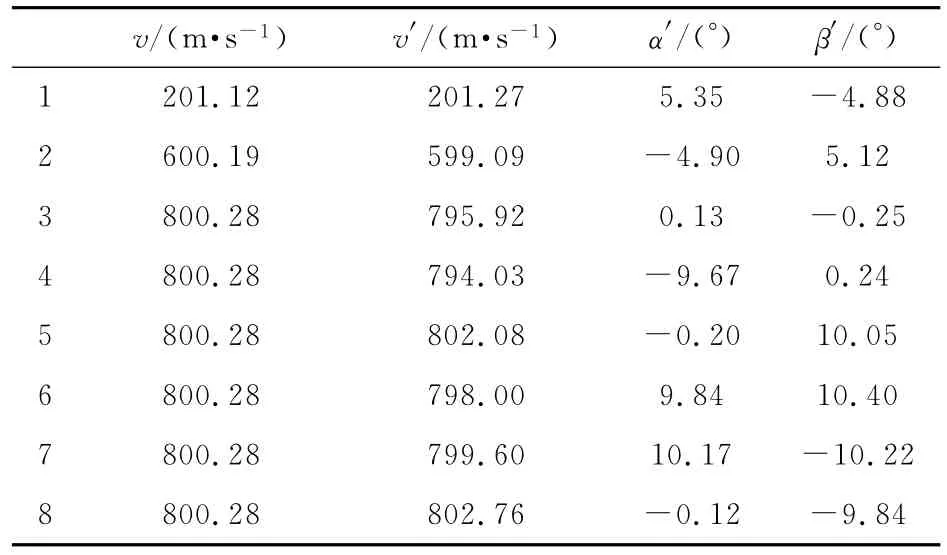
表3 彈丸速度與姿態參數測量值

由表3的測量結果對比表1可知，合速度的相對測量誤差小于2%，姿態的測量最大誤差小于0.4°，平均偏差為0.20°.

4 結論與展望

在本文的測量方法中，彈丸目標的初始時刻在測量坐標系中的位置Xo、Yo、Zo，并不是待求參數，但是為了能夠從嚴格投影方程的角度來分析彈丸的運動和姿態，該參數向量的引入是有必要的.

本文利用成像方程和從目標表面選取的若干個特征點建立了以目標的初始位置、速度和姿態參數共8個未知量的非線性方程組.通過將方程組的求解問題進行最優化建模和求解，實現了各參數的測量.在求解過程中，首先利用了方程組中大量參數是線性的這一特性，以Powell搜索為基礎，同時利用原方程對線性參數進行求解，得到了方程組的一組近似解；然后進一步使用Gauss－Newton迭代法對待求參數進行精確求解.本文方法的優勢體現在：①將線陣像機的嚴格成像方程引入彈丸姿態參數的測量中，使測量方法有嚴格的理論依據；②在嚴格成像模型下，給出了基于特征點坐標的彈丸目標初始位置、速度和姿態參數的解算方法.

考慮到像機鏡頭的光學畸變，在圖像預處理的過程中根據像機標定所得的徑向與切向畸變系數進行預先矯正，因此本文在對像機成像模型的討論中并未涉及畸變模型.

在具體的靶場實踐中采用本文測量方法，可能為測量引入較大的誤差的因素主要有：①目標在經過線陣像機視平面過程中的勻速特性；②像機成像中的積分時間帶來的圖像點模糊；③人工拾取特征點的不確定性.量化研究并盡量消除上述因素對測量精度造成的影響是下一步需要研究的重點內容.此外，本文測量方法只針對具有旋轉體結構的彈丸目標而設計，而對于一般結構的三維目標，由于其空間姿態需要3個空間旋轉進行描述，在使用本文測量基本原理的情況下，需要為之設計新的解算方法.

[1]高昕，王建軍，湯陽.利用狹縫相機實現彈丸攻角高精度測量研究[J].飛行器測控學報，2004，23（1）：69－72.GAO Xin，WANG Jian－jun，TANG Yang.Precision measurement of nutation angle using slit cameras[J].Journal of Spacecraft TT ＆ C Technology，2004，23（1）：69－72.（in Chinese）

[2]張三喜，薛以輝，盧宇.狹縫攝影膠片圖像運動參數測量和處理[J].光子學報，1999，28（12）：1 117－1 121.ZHANG San－xi，XUE Yi－hui，LU Yu.The measuring and processing of streak camera’s image motion parameters[M].ACTA Photonica Sinica，1999，28（12）：1 117－1 121.（in Chinese）

[3]LI J K，CHEN L Y.A slit photography system based on linear CCD[J].Laser ＆Infrared，2009，39（3）：300－303.

[4]SONG W D.Software design for measurement of bullet attitude based on linear CCD[C].9th International Conference on Electronic Measurement and Instruments.Xi’an：CIE，2007：521－524.

[5]HUGHETT P.Projectile velocity and spin rate by image processing of synchro－ballistic photography[C].Ultrahigh－and High－Speed Photography，Videography，Photonics and Velocimetry.San Diego：SPIE，1990：237－248.

[6]RADU H，ROGER M，BOGUSLAW L.On Single－scanline camera calibration[J].IEEE Transactions on Robobtics and Automatic，1993，9（1）：71－75.

[7]LUNA C A，MAZO M，LAZARO J L.Calibration of line－scan camera[J].IEEE Transactions on Instruementation and Measurement，2010，59（8）：2 185－2 190.

[8]馮文灝.近景攝影測量——物體外形與運動狀態的攝影法測定[M].武漢：武漢大學出版社，2007：72－73.FENG Wen－hao.Close－range photogrammetry（measurement of object’s facade and motion）[M].Wuhan：Wuhan University Press，2007：72－73.（in Chinese）

[9]WANG Zhi－zhuo.Principles of photogrammetry[M].Press of Wuhan Technical University of Surveying and Mapping ＆Publishing House of Surveying and Mapping of Beijing，1990：18－19.