空投雷彈斜入水初始彈道數值分析

王永虎，石秀華

（1.中國民航飛行學院，四川 廣漢618307；2.西北工業大學 航海學院，西安710072）

自從上世紀20年代末水上飛機的水面降落問題提出以來，結構物入水沖擊的理論與試驗研究得到了飛速發展，例如，水上飛機和宇宙飛船水面著陸、衛星海面回收、空投雷彈入水沖擊、船舶在風浪中砰擊和救生艇的海上拋落等[1，2].由于理論分析入水初始彈道比較困難，忽撲行為的研究也只局限于定性分析，所以入水初始彈道和忽撲在空投雷彈入水沖擊問題中的研究就顯得尤為重要.20世紀60年代，WAUGH J G在假雷和實雷實驗基礎上，對空投雷彈入水彈道和忽撲行為進行了研究[2，3].為了研究空投水雷的入水以及水下運動行為機理，達到更準確地布雷，MANN J L采用蒙特卡羅法獲得三維水雷模型 MINE6D的運動軌跡[4].CHU P C等建立時域3DOF運動方程以及回歸模型，對圓柱體跌落入水進行了理論分析和實驗研究[5，6].PARK Man－sung等[7]利用面元法數值計算了正切尖拱體以任意角度入水的沖擊載荷，然后對尖拱體的忽撲行為進行了數值計算分析，但是在數值計算中忽略了入水空泡對入水彈道的影響，計算結果不可避免地存在誤差.由于空投雷彈斜入水的復雜性和特殊性，必須對其入水初始彈道進行準確分析以確保斜入水的航行安全性.

1 入水沖擊顯式動力模型

用數理解析方法和數值方法研究入水初始彈道問題時，必須把結構動力學方程和流體動力學方程耦合起來求解，解析方法只適應于簡化模型，而數值模擬應用范圍更廣.LS－DYNA是以顯式為主、隱式為輔的非線性動力有限元仿真軟件，程序中的單元采用拉格朗日列式增量解法，特別適合求解各種二維、三維非線性動力沖擊問題，并與實驗進行無數次的對比，證實了模擬計算的可靠性[8].下面首先根據多物質流固耦合方法，建立斜入水沖擊顯式動力模型；然后數值模擬入水沖擊過程，最后應用到入水初始彈道問題的研究中.

1.1 固體域網格劃分

在入水沖擊的顯式動力模型中，采用有限元方法離散入水結構體（固體域），其有限元方程為

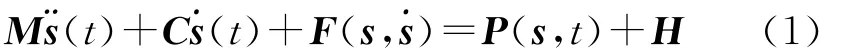
式中，M為總質量矩陣；C為結構阻尼系數；P為總體載荷矢量；F為單元應力場等效節點力矢量組；H為總體結構沙漏粘性阻尼力（t）為總體節點加速度矢量（t）為總體節點速度矢量.

為了真實模擬入水沖擊的液面隆起現象，并提高數值計算速度，求解算法上采用LS－DYNA程序中的多物質ALE算法.由于無反射邊界只能施加到實體單元上，入水結構體采用LS－DYNA單元庫中的六面體SOLID164體元模擬.為了與水域、空氣域耦合，固體域的網格劃分采用Lagrange網格算法.如果結構體外形特殊（例如尖拱體），需采用布爾運算劃分網格，對尖拱體進行了八節點體元網格劃分.同時，為了節省計時，采用沙漏粘性阻尼方式控制單點積分引起沙漏模式，這對模擬液面隆起和飛濺等大變形現象十分有效.由于只討論入水初始彈道，所以將空投雷彈結構外形簡化為圖1所示的數值模型.

在數值計算過程中，采用LS－DYNA的中心差分時間積分的顯式方法，計算系統各節點在第n時間步時刻的加速度a、速度v和位移s分別為

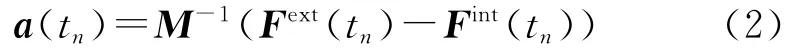
式中，Fext為節點外力和體力矩陣，Fint為節點內力矩陣.

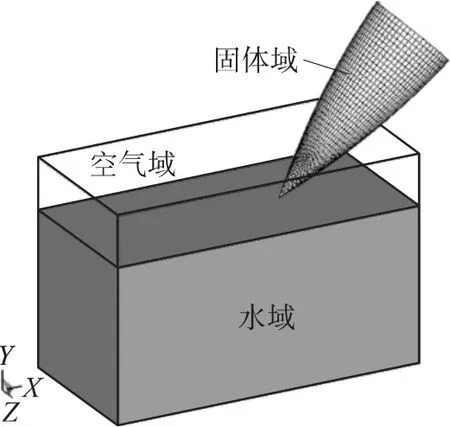
圖1 空投雷彈斜入水沖擊數值模型及計算域

1.2 流體域網格劃分

空投雷彈入水沖擊涉及到三相介質：固體域、空氣域和水域.空氣域和水域均采用LS－DYNA中的空材料模式＊MAT＿NULL來描述，即用本構模型和狀態方程來同時描述流體材料，通過Gruneisen狀態方程確定壓力－體積的關系式：

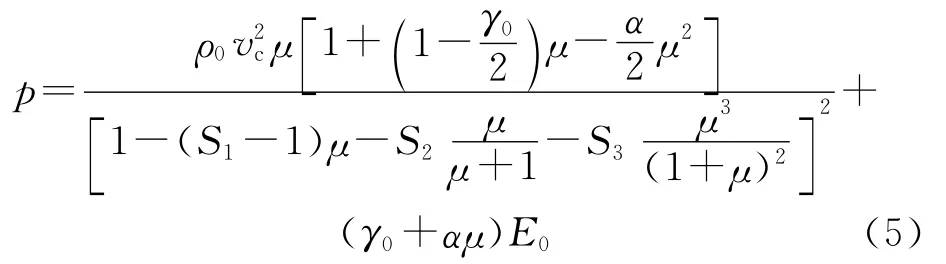
式中，ρ0為材料密度；vc為沖擊波速度；E0為單位體積內能；S1、S2、S3、γ0為材料常數；μ為密度變化率；α為一階體積修正.在LS－DYNA中采用＊EOS＿GUNEISEN關鍵字定義，其中水和空氣2種流體采用Euler網格建模，建模時水和空氣介質均使用映射方法劃分網格.流體材料本構模型和狀態方程具體參數分別見表1，本文數值模型采用cm－g－μs單位制，流體材料本構模型和狀態方程具體參數分別見表1.

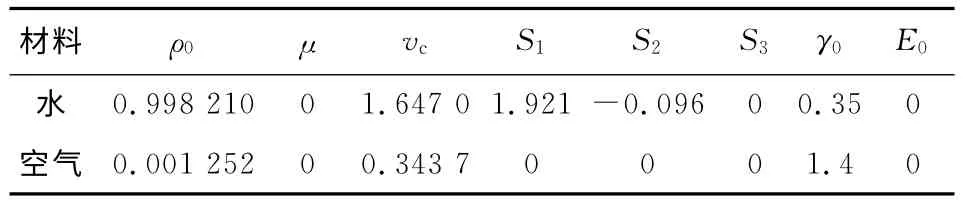
表1 流體材料的本構模型和狀態方程的相關參數

1.3 流固耦合ALE算法

本文采用ALE算法，結合Euler算法與Lagrange算法的優點，結構采用Lagrange單元算法，流體采用Euler/ALE多物質單元算法.ALE算法先執行一個或幾個Lagrange時步計算，單元網格隨材料流動而產生變形.然后，為了保持變形后的物質邊界條件，對內部單元重新劃分網格，將變形網格中的單元變量（密度、能量、應力張量等）和接點速度矢量輸運到重分后的新網格中，最后執行ALE時步計算.特點是耦合面隨著Lagrange單元和Euler單元形成的共同邊界產生運動變形，Euler單元也就可以隨著結構大范圍移動，保證了數值計算順利進行，且大大節約計時.

LS－DYNA程序中的多物質ALE－Lagrange算法可以傳遞ALE網格中的流體材料和Lagrange結構體間的接觸力，能方便地通過＊CONSTRAINED＿LAGRANGE＿IN＿SOLID關鍵字把流體和固體單元進行耦合，且建模時流體網格和固體網格可以交叉重疊.通過＊SECTION＿SOILD＿ALE關鍵字來定義單元算法類型并標識相關單元算法.為了更接近模擬無限水域的分析情況，在流體單元的邊界上定義無反射邊界條件來簡化入水沖擊模型.

1.4 網格劃分尺寸控制

流體網格密度對數值結果是有影響的，理論上講網格劃分越細，數值計算結果越接近真實值，但實際中細密的網格劃分會造成數值計算中誤差累積、結果偏離和計時延長.考慮到計算機允許的計算能力和工程應用的精度要求，合理確定網格密度和計算規模是非常必要的.

為了確定最佳的網格密度，并捕捉應力場的最大梯度變化，這里采用一個無量綱參量來描述網格密度，定義Euler－Lagrange單元網格尺寸比為

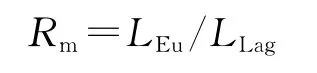
式中，LEu為Euler單元網格特征尺寸；LLag為Lagrange單元網格特征尺寸.一般而言，尺寸比的選取以在仿真過程中數值收斂性好，計算結果較精確為準.這里對Rm＝0.4～0.9的情況進行了數值計算，計算結果見圖2，圖中Cd為入水沖擊阻力系數.

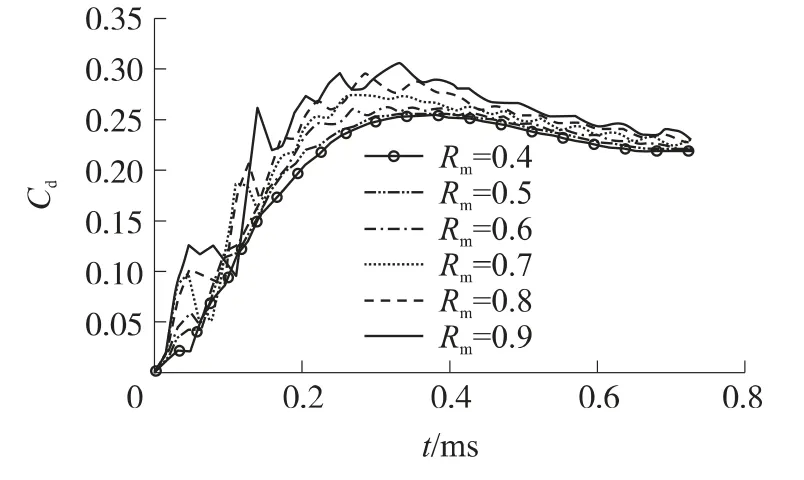
圖2 不同Rm的計算精度曲線

由圖2可以看出，隨著尺寸比的減少，曲線震蕩明顯減弱，而且入水沖擊載荷峰值也在減少，當Rm＝0.6時曲線趨于平穩，當Rm＝0.4時得到最穩定的曲線.數值計算效益和經濟性不僅要考慮結果的精確度，而且要看計算消耗的機時和存取容量.雖然Rm＝0.4的結果較精確，但計時較長和存儲容量驟然增大.因此，這里在空投雷彈入水沖擊數值計算中，Rm取0.5～0.6較合理，故本文后續的彈道分析均采用Rm＝0.6.

2 計算結果與分析

為了便于模型的建立和高效的數值求解，這里主要分析空投雷彈二維入水運動學行為，即入水初始彈道，將結構體定義為剛性體以減少自由度的數量，每次數值仿真的固體域的尺寸和網格劃分方法都不變.為了保證入水彈道軌跡和射流飛濺大部分出現在流體域中，根據入水初始彈道時間和水平距離確定流體域尺寸，這樣會導致每次數值計算中網格數量不一致，但不影響數值仿真結果的準確性.

尖拱體斜入水的初始條件和物理參數為：根據空投雷彈的實際質量，設定尖拱體質量為18.4kg，局部坐標系中質心的轉動慣量在K文件中設定為＊DIM，Ivert，ARRAY，6，1，1，，，、＊SET，IVERT（1，1，1），5189233、＊SET，IVERT （4，1，1），2312606、＊SET，IVERT（6，1，1），5189233，單位為cm－g－μs.數值計算得到各情況下的入水初始彈道，并通過二維圖來表示.

首先，為了研究入水角對忽撲行為的影響，在初始入水速度為100m/s，初始攻角為0，對入水角分別以10°、20°和30°的初始彈道進行模擬.采用尖拱頂點運動軌跡來形象顯示水下初始彈道，見圖3所示.可以看出，入水角越小，運動軌跡越偏離初始軌道；也表明入水角越小，尖拱體越容易產生忽撲行為甚至彈跳，與文獻[7]采用面元法的數值結果吻合，究其原因是入水角小的尖拱體在入水過程中受到的縱傾力矩大.

然后，對質量為18.4kg尖拱體以固定的30°入水角且零攻角情況下的斜入水進行數值仿真，選擇入 水 初 速 度v0分 別 為 30.48 m/s，60 m/s 和100m/s，分析初始速度對入水初始彈道的影響，見圖4所示，圖中顯示的是二維Oxy坐標系中頂點運動軌跡.可以看出，雖然入水速度不同，但只要攻角和入水角不變，尖拱頂點的運動軌跡是相同的，即入水角對入水初始彈道的影響微乎其微.圖5給出了不同質量的尖拱體在v0＝100m/s和相同時間情況下的入水初始彈道二維圖，可以看出，隨著入水體質量的增加，在相同時間內，質量小的尖拱體入水初始彈道曲率較大，從而很容易產生忽撲或彈跳行為.

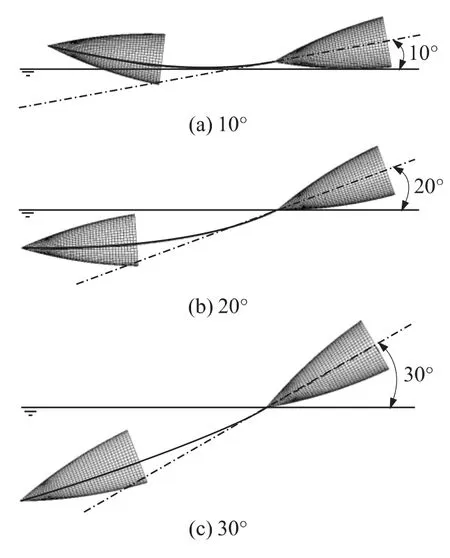
圖3 以相應入水角入水的初始彈道

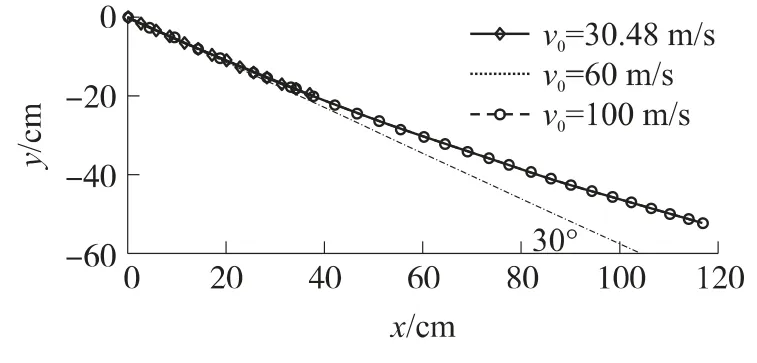
圖4 入水速度不同的入水初始彈道

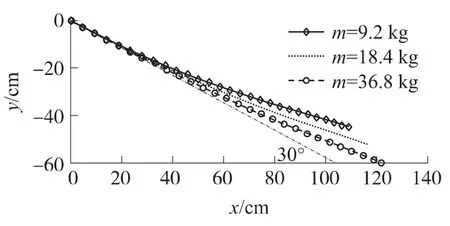
圖5 質量不同的入水初始彈道

最后，空投雷彈與流體剛剛接觸的時候具有一定的入水攻角，這里數值分析了初始攻角對入水運動初始軌跡的影響，見圖6所示.分別選取了3種情況進行模擬仿真，即入水攻角α0分別為－5°、0°和5°，入水初始速度為100m/s，入水角為固定的30°.

從仿真結果可以看出，在入水初速度和入水角速度一定的條件下，入水初始攻角對入水初始運動軌跡和姿態角變化影響較大.正攻角入水使雷彈往拉平方向運動，加劇忽撲甚至出現彈跳行為；負攻角入水使雷彈具有俯沖下潛的趨勢，起到抑制的作用.所以，在小角度斜入水過程中應注意入水攻角的影響作用.

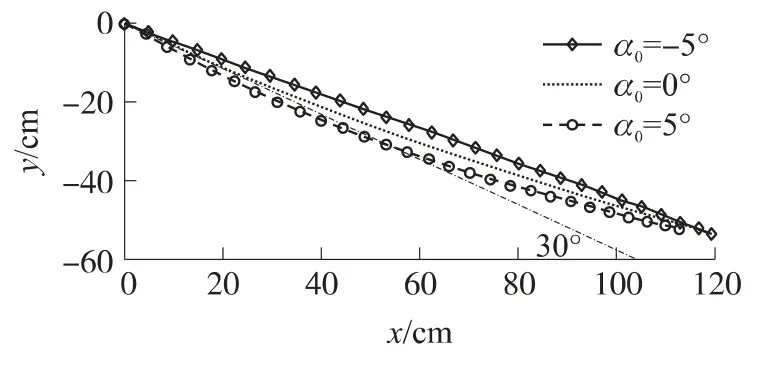
圖6 初始攻角不同的水下初始彈道

3 結論

采用ANSYS/LS－DYNA大型非線性顯式動力程序進行空投雷彈斜入水初始彈道模擬研究，實現入水空泡生成和擴展現象以及不正常入水造成的忽撲行為模擬，考慮了初始條件和物理條件對斜入水初始彈道的影響，得到以下結論：①入水角對入水初始彈道影響很大，如果入水角很小可能產生忽撲行為甚至彈跳行為，這對空投雷彈而言是不利的影響因素；②入水初速度對入水初始彈道幾乎沒有什么影響，空投雷彈都是沿著近似相同的彈道運行；③空投雷彈自身的質量對入水初始彈道也有影響，在其他條件相同的條件下質量越小越容易產生忽撲行為；④對帶有攻角姿態而言，攻角大小對初始彈道有不同的影響，特別針對小角度斜入水情況，可以考慮采用適當攻角來彌補小角度帶來的負面影響，此入水初始彈道規律將指導后續的入水彈道定性或定量分析.

[1]WANG Y，SHI X，WANG P.Dynamical response analysis of incautious water entry of UUV based on exact body shape approach[C].7th World Congress on Intelligent Control and Automation.Chongqing，China：IEEE，2008：4 870－4 875.

[2]WAUGH J G.Water－entry pitch modeling[J].Journal of Hydronautics，1968，2（2）：87－92.

[3]WAUGH J G，STUBSTAD G W.Hydroballistics modeling，AD A007529[R].1975.

[4]MANN J L.Deterministic and stochastic modeling of the water entry and descent of three－dimensional cylinderical bodies[D].USA：Massachusetts Institute of Technology，2005.

[5]CHU P C，FAN C W.3Drigid body impact burial prediction model[J].Advances in Mechanics，2004，5：43－52.

[6]CHU P C，FAN C W.Pseudo－cylinder parameterization for mine impact burial prediction[J].Journal of Fluids Engineering，2005，127：1 515－1 520.

[7]PARK Man－sung，JUNG Young－rae.Numerical study of impact force and ricochet behavior of high speed water－entry bodies[J].Computers ＆ Fluids，2003，32：939－951.

[8]HALLQUIST J O.LS－DYNA theoretical manual[M].Livermore，California：Livermore Software Technology Corporation，2006.