變后掠翼航彈滑翔彈道優化設計

李偉明，孫瑞勝，吳軍基，劉鵬云

（南京理工大學 能源與動力工程學院，南京210094）

變后掠翼航彈與固定翼航彈相比具有更強的生存和突防能力，其彈翼后掠角可根據飛行條件及作戰任務的不同而變化，這使航彈可在更大的空域和速域內飛行[1]，以實現亞、跨、超音速，大包線、低能耗的作戰要求.為了充分發揮變后掠翼航彈飛行性能的優勢，對變后掠翼航彈進行彈道優化具有重要的實際意義.

目前變后掠翼技術在導彈設計中的應用研究是國內外的熱點方向，文獻[2～5]分別從作動機構、理論分析和數值計算等角度深入研究了變后掠翼對飛行器氣動特性的改善問題.在彈道優化方面，文獻[6]針對導彈爬升－轉彎段彈道優化問題，提出了一種利用具有動態初始化策略的粒子群算法對攻角指令進行優化的設計方案；文獻[7]將彈道問題轉化為最優控制問題，采用遺傳算法對高超音速導彈的最優攻角控制律尋優以達到增程的目的；文獻[8]采用縱向加速度優化指令來減小由重力引起的視線角速度誤差，從而提高尋的制導精度.然而傳統的彈道優化多為通過單變量控制來實現彈道增程，本文針對航彈在不同后掠角時的氣動特性，提出了通過攻角及后掠角雙控制量優化滑翔段彈道的方案，同時，為防止陷入局部最優，采用粒子群算法對控制量進行全局尋優.仿真結果表明，增程效果明顯且彈道特性得到相應的改善，可見該方法是合理的、有效的.

1 變后掠翼航彈滑翔彈道模型

1.1 彈道模型

在無風、忽略地球自轉影響、對稱飛行的情況下，航彈在縱向平面內的彈道方程為

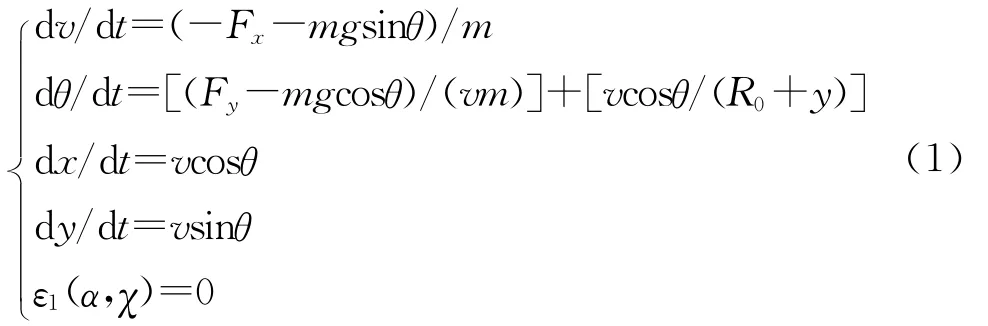
式中，速度v＝Mac，Ma為馬赫數；c為聲速；R0為地球半徑；θ為彈道傾角；阻力Fx＝qSCx，升力Fy＝qSCy，它們由動壓q、參考面積S和氣動特性決定，阻力系數Cx、升力系數Cy是攻角α、后掠角χ和Ma的函數，其值可由吹風試驗和數值計算獲得；ε1（α，χ）＝0為控制方程.

1.2 變后掠翼氣動特性分析

圖1、圖2分別給出了Ma＝1.4時，Cx、Cy隨α和χ的變化關系.可以看出，當α取定值時，Cx隨χ遞減，與χ近似成線性關系；而當χ取定值時，Cx隨α遞增，與α近似成線性關系.Cy是χ的二次函數，在0°≤α≤4°的條件下，Cy的最大值取在χ＝55°處，即可變后掠彈翼處于半展開狀態；而在4°≤α≤8°時，Cy的最大值隨著α的增大向小后掠角狀態偏移.

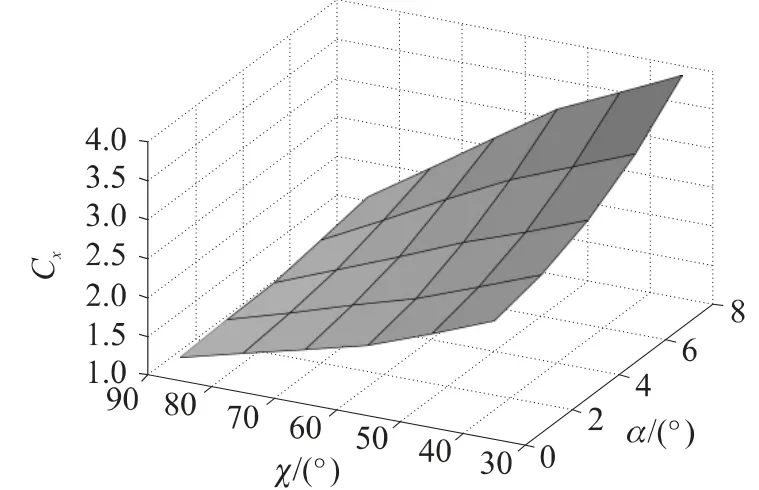
圖1 阻力系數曲面圖（Ma＝1.4）

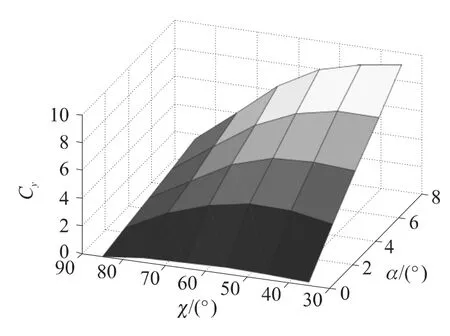
圖2 升力系數曲面圖（Ma＝1.4）

圖3、圖4分別給出了Ma為0.8和1.8時，航彈升阻比隨α和χ的變化關系.可看出，升阻比隨α和χ成非凸域分布，最大升阻比隨Ma遞減，且Ma越大，升阻比非線性程度越明顯.另外，在Ma與α為定值時，最大升阻比與χ呈開口向下的拋物線關系.

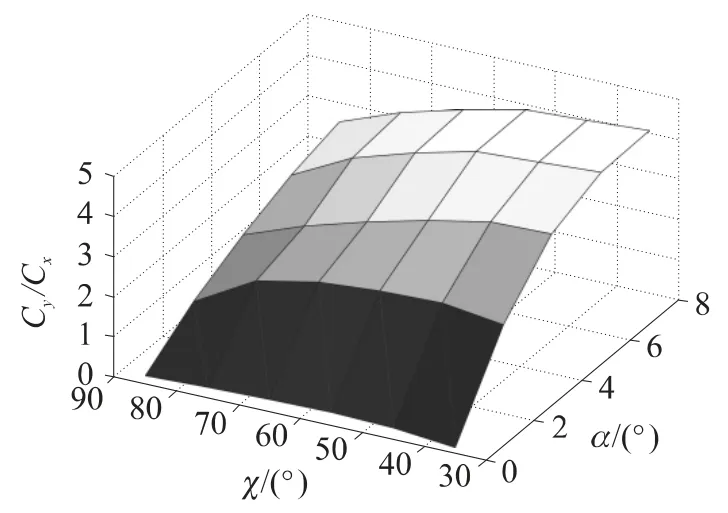
圖3 升阻比曲面圖（Ma＝0.8）

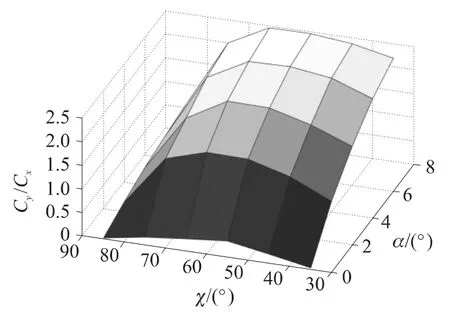
圖4 升阻比曲面圖（Ma＝1.8）

2 彈道優化算法

2.1 性能指標及Hamilton函數

依據滑翔段彈道優化原理，航彈滑翔段飛行彈道距離最遠問題是在飛行初始、末端狀態已知的情況下，如何確定α（t）與χ（t）的控制律問題.因此，航彈滑翔段彈道優化的目標函數為滑翔段的水平飛行距離最大，數學描述為

該性能指標可通過優化算法對α（t）及χ（t）全局尋優的方法來實現.

根據式（1）和式（2）構造對應的Hamilton函數為

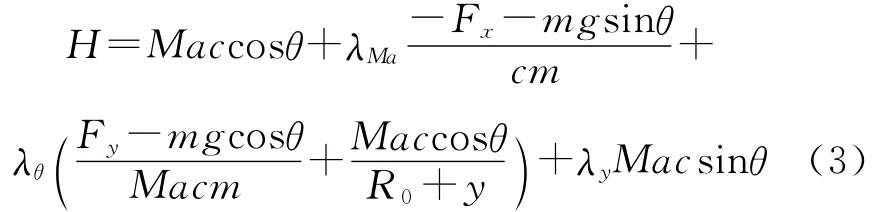
式中，λ為待定拉格朗日乘子.其歐拉方程為

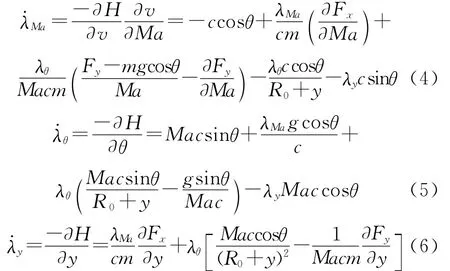
式中，

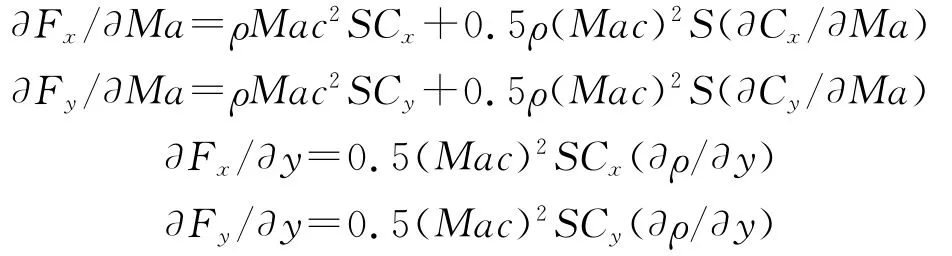
式中，?Cx/?Ma、?Cy/?Ma可通過吹風試驗數據及數值計算擬合得到；密度ρ＝ρ0（1－2.032 3×10－5y）4.83，地球表面大氣密度ρ0＝1.225kg/m3.

由Hamilton方程（3）可得：

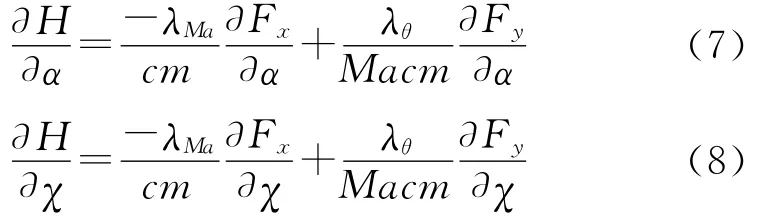
式中，

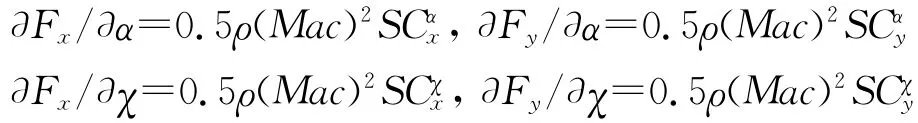
分別為阻力系數、升力系數關于攻角的導數分別為阻力系數、升力系數關于后掠角的導數.以上各值可通過吹風試驗數據及數值計算擬合得到.

由極值條件?H/?α＝0和?H/?χ＝0，可得：

式（9）、式（10）可作為優化算法對α（t）、χ（t）尋優的目標函數.

邊界約束條件為

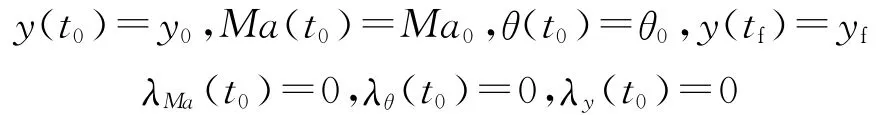
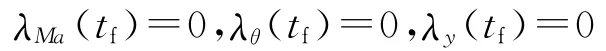
2.2 粒子群（PSO）優化算法

粒子群算法（PSO）[9]是一種基于群體智能的非數值并行算法，實現容易且精度高，克服了局部尋優方法的優化結果對初值敏感的缺陷，可全局尋優.

設N維目標搜索空間Xi中的群體由M個粒子構成，粒子的進化方程為

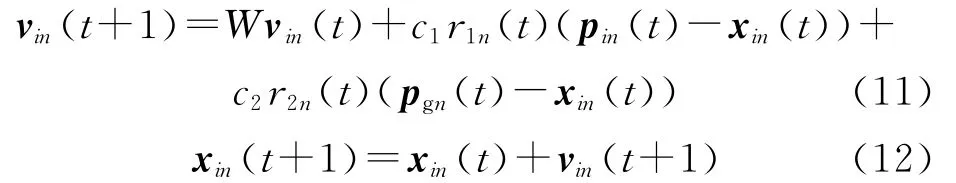
式中，n＝1，2，…，N；t為迭代次數；W為慣性權重；r1n、r2n為[0，1]之間的隨機數；c1、c2為學習因子；xin為第i個粒子的位置矢量；vin為粒子i的飛行速度；pin為個體極值；pgn為最優極值.

為確保對極值條件式（9）、式（10）中的α（t）和χ（t）同時尋優，本文引入權重系數σ1、σ2，將適應度函數改寫為

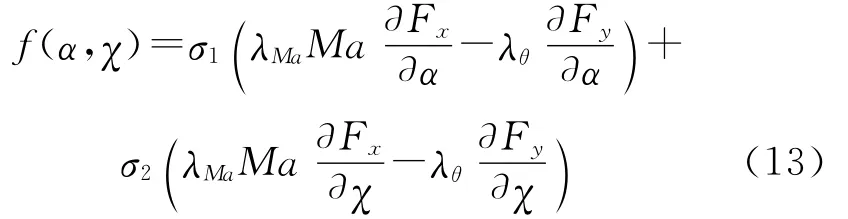
式中，σ1＋σ2＝1.

3 仿真算例

以某變后掠翼航彈為例進行滑翔彈道優化設計，給定初始高度y0＝12km，初始馬赫數Ma0＝2，初始彈道傾角θ0＝0°，滑翔段末端高度yf＝5km.由于該航彈后掠角變化范圍為[35°，85°]，在使用上述算法進行優化時，以χ/10、α為2維粒子變量，取M＝20，N＝2，最大迭代次數為500，W＝2，c1＝c2＝1.628.為防止粒子離開搜索空間，將搜索空間Xi限定在[0，9]內，粒子進化速度vi限定在[－9，9]內.

圖5～圖9分別給出了采用本方法實現的最優控制算法和2種次優算法的滑翔段彈道對比曲線.次優方案①為固定外形：定后掠角χ（t）＝35°、攻角α（t）單變量控制；次優方案②為單變量可變后掠外形：定攻角α（t）＝2.5°、后掠角χ（t）單變量控制.從圖中可看出，在同樣的初始條件和約束條件下，最優方案所優化出的彈道飛行距離較次優方案①多13.809km，較次優方案②多6.27km，具有明顯的增程效果.相對于攻角α（t）單變量控制，雙變量優化使得攻角變化較平緩且能始終保持在小角度范圍內變化.從圖6、圖7可看出，采用最優方案對α（t）及χ（t）尋優時，其結果符合變后掠翼航彈升阻比最大的分布規律，充分挖掘了航道動力學潛能，尋優結果正確，方法可行.

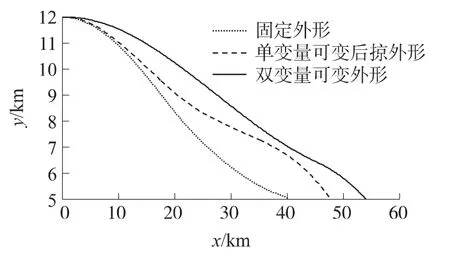
圖5 滑翔段彈道軌跡比較圖

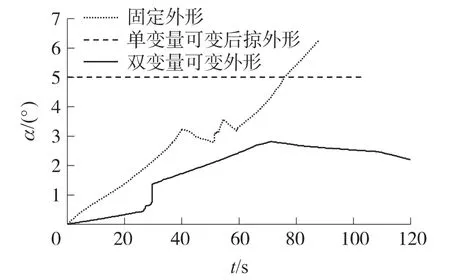
圖6 攻角變化曲線

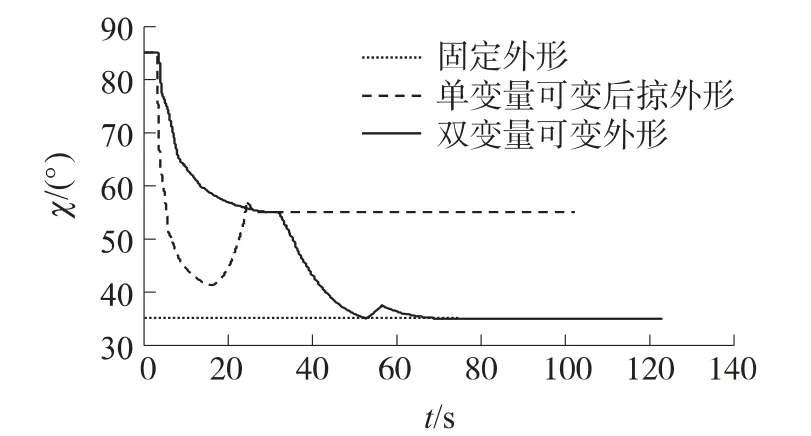
圖7 后掠角變化曲線

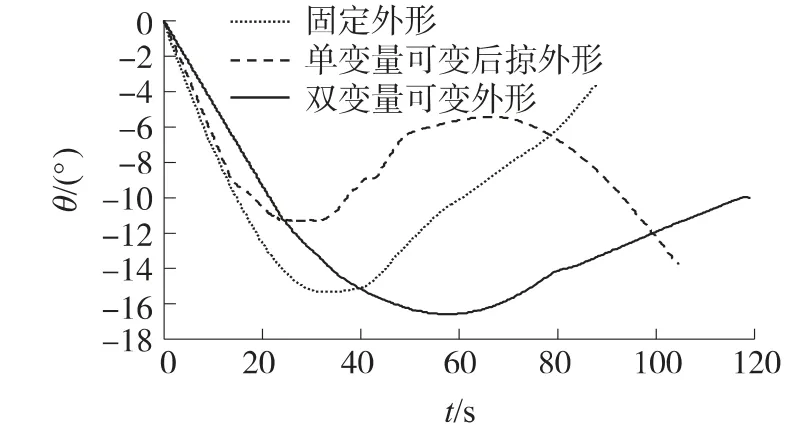
圖8 彈道傾角變化曲線

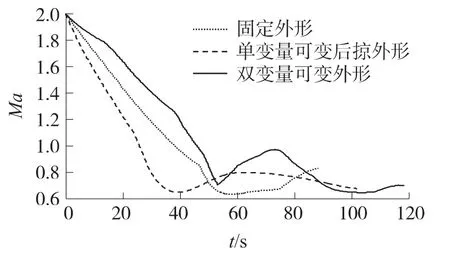
圖9 飛行速度變化曲線

4 結束語

本文以某機載變后掠翼航彈滑翔增程段彈道為研究對象，結合最優控制與PSO算法進行彈道優化，分析了氣動力系數隨后掠角和攻角的變化規律，給出了后掠角及攻角控制量在增程中的控制規律，通過數值仿真驗證了該增程優化方案的正確性和可行性，可為變后掠翼航彈的總體設計提供理論參考.

[1]TAKAHASHI T T，SPALL R J.A multi－disciplinary assessment of morphing aircraft technology applied to tactical cruise missile configuations，AIAA 2004－1725[R].2004.

[2]MARMIER P，WERELEY N M.Morphing wings of a small scale UAV using inflatable actuators sweep control，AIAA 2003－1802[R].2003.

[3]TAKAHASHI T T，SPALL R J，TUMER D C，et al.A multidisciplinary survey of advanced subsonic tactical cruise missile configurations，AIAA 2005－0709[R].2005.

[4]SNYDER M P.Vibration and flutter characteristics of a folding wing[J].Journal of Aircraft，2009，46（3）：791－799.

[5]TANG L，BARTEL R E.Simulation of transonic limit cycle oscillations using a CFD time－marching method[C].42th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics and Materials Conference ＆ Exhibit.Seattle，WA：AIAA，2001：1 263－1 265.

[6]郭杰，唐勝景，李響，等.基于改進粒子群算法的方案飛行彈道優化設計[J].北京理工大學學報，2010，30（6）：688－692.GUO Jie，TANG Sheng－jing，LI Xiang，et al.Optimum design of the project trajectory based on an improved particle swarm optimization[J].Transactions of Beijing Institute of Technology，2010，30（6）：688－692.（in Chinese）

[7]孫瑞勝，薛曉中，沈堅平.一種乘波外形導彈增程段彈道的最優控制解法[J].彈道學報，2008，20（4）：57－60.SUN Rui－sheng，XUE Xiao－zhong，SHEN Jian－ping.Trajectory optimization for a hypersonic waverider missile in extended range period by means of optimal control[J].Journal of Ballistics，2008，20（4）：57－60.（in Chinese）

[8]王紅偉，唐碩，方慧，等.尋的防空導彈的一種彈道優化方法[J].彈道學報，2006，18（3）：22－25.WANG Wei－hong，TANG Shuo，FANG Hui，et al.A method of trajectory optimization for homing antiaircraft missle[J].Journal of Ballistics，2006，18（3）：22－25.（in Chinese）

[9]KENNEDY J，EBERHART R.Particle swarm optimization[C].Proc of IEEE Int Conf on Neural Networks.Piscataway，NJ：IEEE，1995：1 942－1 948.