周期性壓力對T型微管內二元流體混合效果的影響*

華 碩， 李 霞， 許友生， 吳鋒民

(1．吉林化工學院 理學院，吉林 吉林 132000，2．浙江師范大學 數理與信息工程學院，浙江 金華321004)

0 引言

二元微流動的混合問題是微流動領域最基礎的問題之一．這個問題廣泛存在于醫藥學、生物學、化學等各個專業領域．

湍流和混沌流的混合效果遠遠高于一般的層流．混沌對流的顯著特征是接觸面的增長及層流厚度的相應減少，其中最簡單的就是漩渦模型．文獻［1］通過實驗研究了彎曲的微管道內的漩渦流和混沌混合，并且展示了簡單的彎曲管道可以引導混沌對流．Simonnet和Groisman［2］完成了微管道內能使層流產生混沌式混合的實驗，并宣布他們提出的微管道能提供更快更有效的混合，并且簡單易行．Pereira［3］研究了可變的滑移邊界條件對非牛頓流體的壓力傳遞的影響，提出了一個方便的方法：通過使用滑移邊界條件結合正弦時間梯度壓力來增加橫流．Ian和Nadine［4］模擬了兩入口呈90°夾角的微管內的二元流體的混合，并發現當流體的入口速度隨時間呈正弦梯度變化時可提高流體混合效果．

本文提出一種新的T型微管道混合器，該混合器僅僅通過流體速度隨時間呈正弦梯度變化來制造混沌流，從而達到促進混合的目的;同時，研究了該混合器在相位差不同、雷諾數不同及速度變化周期不同情況下的混合效果．

1 二元混合物的格子玻爾茲曼模型

本文采用文獻［5-6］的模型模擬二元流體的混合．對于二元流體系統內的2種物質，能得到2個玻爾茲曼方程［6］：

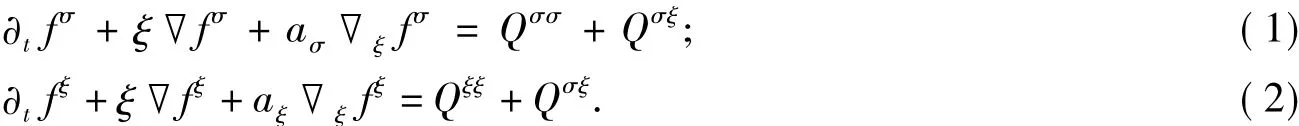
式(1)～式(2)中：f是概率分布函數;ξ是粒子速度;σ和ξ代表2種物質;Qσξ是由于2種物質相互作用的碰撞項;Qσσ和Qξξ是自碰撞項．格子玻爾茲曼方程可被離散為如下形式：

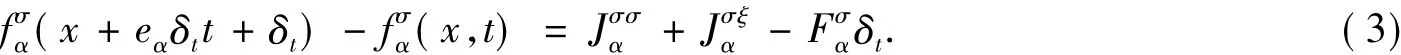
自碰撞項的得出類似于單流體LBM(Lattice Boltzmann Method)，并且也采用BGK(Bhatnagar-Gross-Krook)模型．在等溫線系統的假設中，互碰撞來源于兩流體理論．碰撞方程的右邊項分別是：

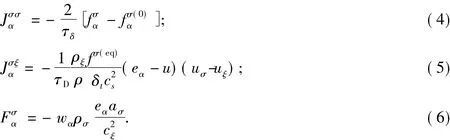
式(4)～式(6)中：Fσα代表外力;ρσ和ρξ，uσ和uξ分別是2種流體σ和ξ的質量密度和流動速度;eα是速度矢量;aσ是加速度;ρ和u是流體的密度和速度，它們的定義分別為 ρ=ρσ+ρξ和 ρu=ρσuσ+ρξuξ．在二元流體混合模型中，兩組分的黏性由松弛因子τσ和τξ調節．對于不可互溶的混合物，τD應該小于0．5，此時，兩流體間有明顯的接觸面．相反，對于模擬可互溶的混合物，τD應該大于0．5．平衡態分布函數 fσ(0)α被定義為：

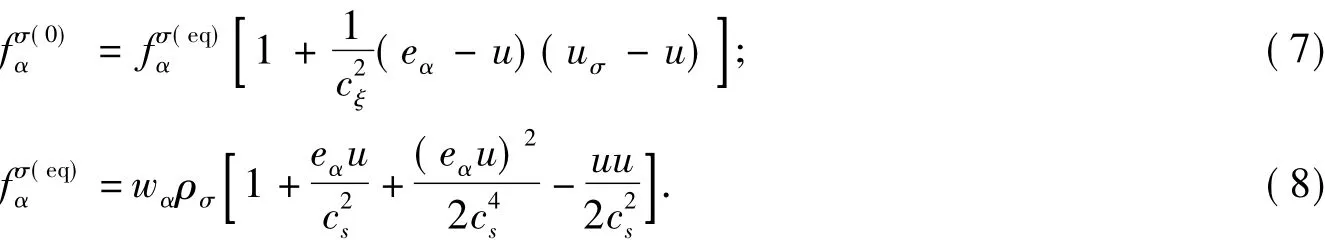
式(8)中：w0=4/9;w1，2，3，4=1/9;w5，6，7，8=1/36．各種類的黏性等對D2Q9模型，速度矢量

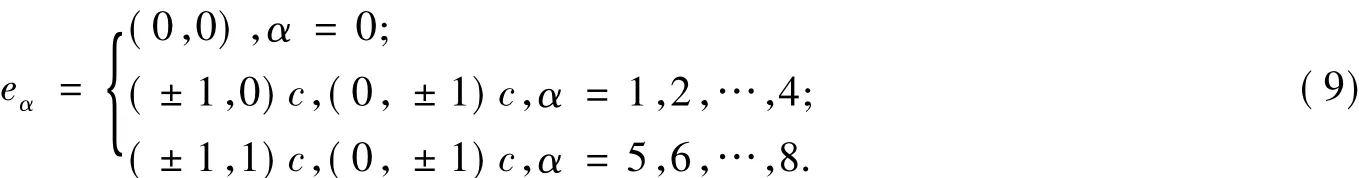
2 初始狀態設置

本文中，每個單元格對應實際長度為1 μm，每計算步對應時間為8．65×10－5s．如圖1所示，本文采用T型微管道混合器，微管的長寬分別為520 μm和120 μm單元格，入口寬度為20 μm．流體A和流體B將以變化的速度分別流入管口，而流速隨時間呈正弦曲線變化，兩入口處速度分別為 va=vmsin(ωt)，vb= －vmsin(ωt+kπ)，其中 k=0，不永遠是正的，當速度值隨時間變為負值時，相當于在管口加一負壓力，即抽吸力．下文將研究入口速度公式中3個可變參數(最大速度vm，速度變化周期T，相位差kπ)的變化對混合效果的影響．

3 計算結果及分析

當兩流體以恒定不變的速度流入T型管時，兩流體趨于層流，混合僅僅通過兩流體接觸面上的分子的自由擴散，效果微弱．為了比較和衡量新型微混合器的混合效果，筆者用黑白兩色分別代表A，B兩流體．由圖2可以明顯看出，A，B兩流體已均勻混合，效果較好．

3．1 相位差對混合效果的影響

圖3顯示的是最大速度 vm=3．0×10－7m/s2種流體基本上都以層流的方式流動．令人驚奇的是，當k=1，即兩入口速度相位差為π時，由圖3(d)可見，兩流體竟然發生了劇烈的攪動——漩渦式的流動．漩渦流是典型的混沌流，而混沌混合是微混合方式中混合效果比較好的一種．

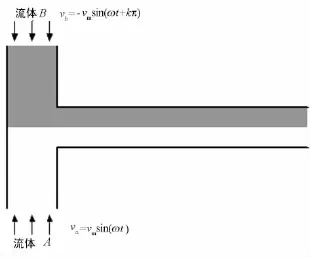
圖1 入口速度隨時間呈正弦梯度變化的T型管示意圖

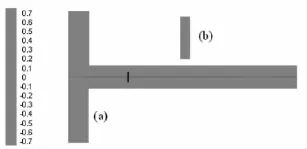
圖2 兩流體勻速流入T型管時的混合效果圖

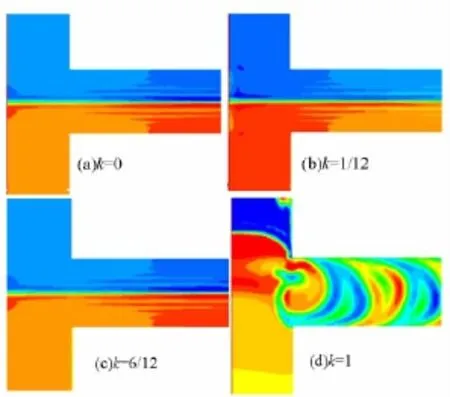
圖3 vm=0．3 ×10－7m/s時，兩入口速度的相位差分別為(0，1/12，6/12，1)π 時的密度圖

產生這一效果的原因其實并不復雜：根據正弦函數的變化規律，當相位差為0，即k=0時，兩流體的入口速度隨時間變化總是大小相等，方向相反．這樣，當兩不可互溶流體以方向相反的速度相遇時，由于自由擴散率低，將對相對交錯流動的排斥力產生極大的阻礙(例如油和水不管如何攪拌，兩組分之間不盡相同，所以也很難交錯流動，而最終只能涇渭分明地平行流過微管道．而k=1，即二流體速度的相位差為π時，兩流體的入口速度總是大小方向均相同．這就造成了一種“你進我退”的共同運動的趨勢．而當兩流體進入主流道時，兩者速度共同發生偏轉，于是就產生了漩渦．

由此可以看出，2種不可互溶流體以相同方向的速度流動時，更容易混合在一起，而不會由于速度方向相反而產生斥力進而影響混合．這就為混合的方式提供了新的思路．以往對流混合總是讓兩流體產生相對的運動速度，使兩者對流、交匯，這使得不可互溶的2種流體產生了較大的速度耗散，且混合效果不明顯．而筆者提出的方法是讓兩流體產生相同方向的速度，并一起震蕩，最終可獲得良好的混合效果．

3．2 速度對混合效果的影響

速度對微流動的影響是非常重要且明顯的．本節將計算當速度最大值 vm分別為 0．3 ×10－7，1．5 ×10－7，3．0 ×10－7m/s時的混合效果．

從圖4可以看出，當最大速度為0．3×10－7m/s時，兩流體僅在交匯處發生輕微擾動，然后涇渭分明地平行流動，其間并未有任何交錯擾動的趨勢．隨時間的變化，混合效果未見提高．這和勻速流體的流動相似．可見，當雷諾數太小時，該混合器將受制于黏滯力的影響，發揮不了作用．

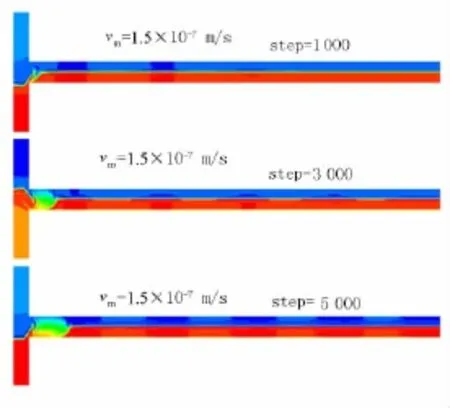
圖 5 vm=1．5 ×10－7m/s，計算步數分別為1 000，3 000，5 000 時流體的密度圖

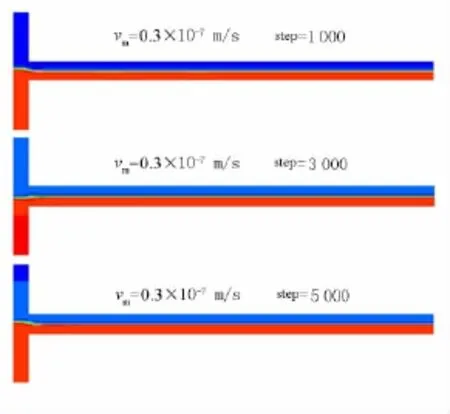
圖 4 vm=0．3 ×10－7m/s，計算步數分別為1 000，3 000，5 000 時流體的密度圖

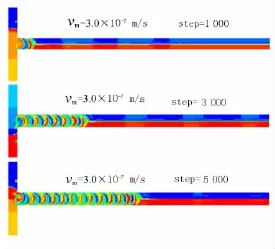
圖6 vm=3．0 ×10－7m/s，計算步數分別為1 000，3 000，5 000 時流體的密度圖

從圖5可以看出，當最大速度達到1．5×10－7m/s時，隨著時間的推移，兩流體間接觸面增大且層流厚度大大減少，混合效果均勻明顯．只是由于慣性力較小，混合進度較慢．

從圖6可以看出，當最大速度達到3．0×10－7m/s時，隨著時間的推移，兩流體混合速度明顯加快，混合效果較均勻．

至此，可以得出結論：當最大速度達到1．5×10－7m/s時，黏性力與慣性力的比例恰好可以使混合較為均勻，但是，混合速度較慢．隨著速度的增大，慣性力增大，發生混沌混合的速度明顯加快，但混合效果變得越來越不均勻．總之，速度對該混合器的混合效果和混合速度有重要影響．

3．3 速度變化快慢對混合效果的影響

管道兩入口速度va=vmsin(ωt)，vb=－vmsin(ωt+kπ)，其中：ω=2π/T;T是衡量速度變化快慢的物理量，數值上等于單位時間步的n倍，而單位時間步對應的實際時間為8．65×10－5s．為了研究速度隨時間變化的快慢對混合效果的影響，下面將模擬當vm=3．0×10－7m/s時，不同的速度變化周期下兩流體的混合效果(見圖7)．

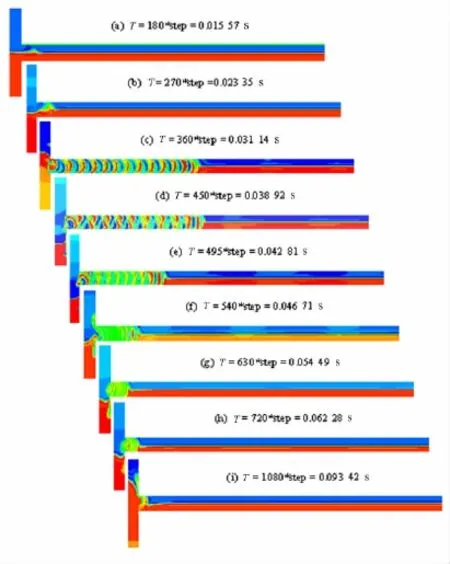
圖7 速度變化周期不同情況下的混合效果

從圖7(a)，(b)可以看出，當速度變化周期過小時(T＜0．023 35 s)，速度變化過快，僅在管道兩入口的交匯處有局部的混合，混合效果不明顯．

當 T ＞0．023 35 s，混合速度明顯加快和混合效果明顯提高．從圖 7(c)，(d)，(e)，(f)，(g)，(h)看到，當T=360*step=0．031 14 s左右時，混合效果明顯且相同時間內混合區域最長．而隨著周期T變長，相同時間內，管道內的混合區域逐漸縮短，但混合效果更均勻．

從圖7中的(i)看出，當周期T＞0．062 28 s，由于速度變化過慢，而兩流體A，B又存在相位差，這就導致兩流體在相當長的時間內速度相差很大，造成管道內一種流體多、另一種流體少，從而影響了混合，混合器失效．

由此可以得出結論：兩流體速度變化的快慢對混合效果有著至關重要的影響，速度變化過快或過慢都有可能導致混合器失效，最適宜的周期長度區間為0．023 35 s＜T＜0．062 28 s．

4 結論

本文提出了一種可以簡單地通過控制入口流速促進二元流產生混沌式混合的T型管混合器，并且研究了該混合器發揮效用的幾個必要條件：

1)兩流體分別以隨時間呈正弦函數變化的速度流入T型微管道的兩入口，兩流體流速的相位差為π．

2)兩流體入口最大速度vm不能過小或過大：過小時，將很難產生波動;過大時，混合速度快，混合效果有所降低．對混合效果來講，存在著最佳的vm值范圍．

3)速度變化周期T的長短也影響著混合效果，T過大或過小都無法令兩流體混合．當最大速度vm=3．0 ×10－7m/s，且0．023 35 s ＜T ＜0．062 28 s時，混合效果最好．

［1］Jiang Minxi，Wang Xiaonan，Ouyang Qi，et al．Spatiotemporal chaos control with a target wave in the complex Ginzburg-Landau equation system［J］．Phys Rev E，2004，69(5)：056202．

［2］Simonnet C，Groisman A．Chaotic mixing in a steady flow in a micro channel［J］．Physical Review Letters，2005，94：134501．

［3］Pereira G G．Effect of variable slip boundary conditions on flows of pressure driven non-Newtonian fluids［J］．J Non-Newtonian Fluid Mech，2009，157(3)：197-206．

［4］Ian G，Nadine A．Enhancement of microfluidic mixing using time pulsing［J］．Lab on a Chip，2003，3：114-120．

［5］Luo Lishi，Girimaji S S．Lattice Boltzmann model for binary mixtures［J］．Phys Rev E，2002，66(3)：035301．

［6］Luo Lishi，Girimaji S S．Theory of the lattice Boltzmann method：Two-fluid model for binary mixtures［J］．Phys Rev E，2003，67(3)：036302．