不含特殊短圈平面圖的無圈邊染色*

鄭麗娜

(浙江師范大學數理與信息工程學院，浙江金華 321004)

0 引言

本文僅考慮有限簡單圖．給定一個圖G，用V(G)，E(G)，Δ(G)，δ(G)分別表示它的頂點集、邊集、最大度、最小度．若uv∈E(G)，則稱點u為點v的鄰點，并用N(v)表示點v的鄰點集合．點 v的度d(v)=|N(v)|;k-點(k+-點，k--點)表示度是k(至少為k，至多為k)的頂點．若能將圖G畫在平面上，使得它的邊僅在端點處相交，則稱G是可平面圖．圖的這種平面圖上的畫法稱為圖的平面嵌入，或稱為平面圖．

圖G的正常k-邊染色是指映射c：E(G)→{1，2，…，k}使得相鄰的邊染不同的顏色;若G有一個k-邊染色，則稱圖G是k-邊可染的;無圈k-邊染色是指圖G的一個正常的k-邊染色，使其不產生雙色圈;無圈邊色數a'(G)是指使得圖G有一個無圈k-邊染色的最小整數k．

無圈邊染色的概念最早是由 Fiamcˇík［1］提出的．Alon 等［2］證明了：對任何圖 G 有 a'(G)≤64Δ(G);Molloy和 Reed［3］將這個界改進到 a'(G)≤16Δ(G);2005 年，Muthu等［4］證明了當 g(G)≥220 時，a'(G)≤4．52Δ(G)．2001 年，Alon 等［5］提出了如下著名的無圈邊染色猜想：

猜想1 對任意圖G，有a'(G)≤Δ(G)+2．

猜想1至今還未得到證實，僅知道一些特殊圖類滿足猜想1．Alon等［6］證明了確定任意圖G的無圈邊色數是一個NP-問題．Cohen等［7］還提出了如下猜想：

猜想2 設G是一個平面圖，則存在一個整數Δ0，使得當Δ(G)≥Δ0時，就有a'(G)=Δ(G)．

對于不含特殊短圈的平面圖，文獻［8］證明了：若G不含4到8-圈，則a'(G)≤Δ(G)+2;文獻［9］證明了：若G不含4-圈，5-圈或G不含4-圈，6-圈，則a'(G)≤Δ(G)+2;文獻［10］證明了：若G不含4到11-圈且Δ(G)≥10或G不含4到9-圈且Δ(G)≥11，則a'(G)≤Δ(G)+1．

本文主要研究了不含特殊短圈平面圖的無圈邊染色問題，得到了以下結果：

定理1 設G是一個平面圖，如果G不含4到8-圈，那么a'(G)≤Δ(G)+1．

1 結構引理

本節討論的全部是平面圖，且假設它們已經嵌入到平面上．設圖G是平面圖，通常用F(G)表示面集;對于f∈F，用d(f)表示面 f的度數;若一個k-面沿著某個方向的點依次為u1，u2，…，uk，則稱這個面為(d(u1)，d(u2)，…，d(uk))-面;k-面(k+-面，k--面)表示度是 k(至少為 k，至多為 k)的面;(i，j，k+)-面表示i-點，j-點和 k+-點相連的3-面，其中i≤j≤k;對G的一個邊染色c和頂點v∈V(G)，設 C(v)={c(uv)|u∈N(v)}．

設圖G是滿足定理1條件的一個邊數極小反例，那么G是2-連通的．否則，設v是G的一個割點，G1，G2，…，Gt(t≥2)是 Gv的連通分支．由 G 的極小性知，對任意1≤i≤t，G'i=Gi∪{v}都有無圈 k-邊染色ci．若點v相關聯的邊出現相同顏色，則通過每個ci進行色置換，使得點v相關聯的邊染不同色，從而可得G的一個無圈k-邊染色，與G的極小性矛盾．

設 k=Δ(G)+1，為方便討論，令顏色集 C={1，2，…，k}．此外，簡記 Δ =Δ(G)．

首先給出一些定理1證明中需要用到的引理．

引理1 若d(v)=2，則v不與3--點相鄰．

證明 假設v與一個3--點u相鄰．設w≠u是v的另一鄰點，G'=G-uv．由G的極小性知，G'有無圈 k-邊染色 c，染色集 C={1，2，…，k}，不妨設 c(vw)=1．

1)若1?C(u)，則用a0∈C(C(u)∪{1})染 uv．因|C(C(u)∪{1})|≥k-3≥1，故這樣的顏色a0存在，且染色c仍是無圈的．

2)1∈C(u)．若存在 a1∈C(C(u)∪C(w))，則用 a1染 uv．否則，設 d(u)=3，u1≠v，u2≠v是 u 的另外 2 個鄰點，c(uu1)=1，c(uu2)=2，A1=C{1，2}．若存在 b0∈A1，使得 G'中不含(1，b0)(u1，w)-雙色路，則用 b0染 uv．否則，假設對于任意 i∈A1，G'中均有(1，i)(u1，w)-雙色路，則 A1?C(w)∩C(u1)．又因d(w)≤Δ，d(u1)≤Δ，故C(w)=C(u1)=C{2}，因此可用2改染vw．與前面討論類似，可設對于任意i∈A1，G'中均有(2，i)(u2，w)-雙色路且 C(u2)=C{1}．此時交換 uu1和 uu2所染的色，再用 3 染 uv，從而可得G的一個無圈 k-邊染色，與G的極小性矛盾．所以，v不與3--點相鄰．引理1證畢．

引理2 若d(v)=d≥4，則v至多與d-2個2-點相鄰．

證明 假設存在一個 d-點v與d-1 個2-點相鄰．設N(v)={u1，u2，…，ud}，d(ui)=2，N(ui)={v，wi}，i=1，2，…，d-1，G'=G-u1v．由 G 的極小性知，G'有無圈 k-邊染色 c，染色集 C={1，2，…，k}，不妨設 c(uiv)=i，i=2，3，…，d．

1)若 c(u1w1)?{2，3，…，d}，則用 a2∈C({2，3，…，d}∪{c(u1w1)})染 u1v．因|C({2，3，…，d}∪{c(u1w1)})|≥k-d≥1，故這樣的顏色a2存在，且染色c仍是無圈的．

2)若 c(u1w1)∈{2，3，…，d-1}，不妨設 c(u1w1)=2，則用 a3∈C({2，3，…，d}∪{c(u2w2)})染u1v．因|C({2，3，…，d}∪{c(u2w2)})|≥k-d≥1，故這樣的顏色 a3存在，且染色 c仍是無圈的．

3)c(u1w1)=d．若存在 a4∈{1，d+1，d+2，…，k}C(w1)，則用 a4染 u1v．否則，{1，d+1，d+2，…，k}?C(w1)．又因為 d(w1)≤Δ 且 d∈C(w1)，所以至少存在1個顏色 j∈{2，3，…，d-1}C(w1)．此時，用 j改染u1w1，用a5∈C({2，3，…，d}∪{c(ujwj)})染u1v，可得G 的一個無圈k-邊染色，與G 的極小性矛盾．所以，v至多與d-2個2-點相鄰．引理2證畢．

引理3 在3-面的邊界上沒有2-點與4-點相鄰．

證明 假設一個2-點u與一個4-點v相鄰在一個3-面uvw的邊界上，G'=G-uv．由G的極小性知，G'有無圈 k-邊染色 c，染色集 C={1，2，…，k}，不妨設 c(uw)=1，c(vw)=2．

1)若1?C(v)，則用 a6∈C(C(v)∪{1})染 uv．因|C(C(v)∪{1})|≥k-4≥1，故這樣的顏色 a6存在，且染色c仍是無圈的．

2)1∈C(v)．設 v1，v3是 v的另外2 個鄰點，c(vv1)=1，c(vv3)=3，A3=C{1，2，3}．若存在 b1∈A3，使得 G'中不含(1，b1)(v1，w)-雙色路，則用 b1染 uv．否則，假設對于任意 j∈A3，G'中均有(1，j)(v1，w)-雙色路，則 A3?C(w)∩C(v1)．又因 d(w)≤Δ，故 C(w)=C{3}．進一步，可假設對于任意 j∈A3，G'中均有(3，j)(v3，w)-雙色路，則 A3?C(w)∩C(v3)．

只需考慮 d(v1)=d(v3)=Δ．顯然有|{1，2，3}∩C(vi)|=2，i=1，3．此時，先抹去 uw 的色．

①若2∈C(v1)∩C(v3)，則交換vv1與 vv3所染的色，用3染uw，再用4染uv．

②若2?C(vi)，i∈{1，3}，即 3∈c(vv1)，1∈c(vv3)，則 C(v1)=C(v3)=C{2}．若 w 到 v1無(2，4)-雙色路，則分別用 2，1 改染 vv1，vw，用3 染 uw，再用4 染uv．若 w 到v1有(2，4)-雙色路，則分別用2，1改染vv3，vw，用3染uw，再用4染uv．由雙色路的唯一性知，w到v3無(2，4)-雙色路．

③若2∈C(v1)，且2?C(v3)，則分別用 3，2，1 改染 vv1，vv3，vw，用3 染 uw，再用 4 染 uv．

綜上，可得G的一個無圈k-邊染色，與G的極小性矛盾．所以，在3-面的邊界上沒有2-點與4-點相鄰．引理3證畢．

引理4 若d(v)=4且v相鄰2個2-點，則v不會關聯3-面．

證明 假設v關聯一個3-面uvw．設x，y是與 v相鄰的2個2-點，x1，y1分別是2-點 x，y的另一鄰點，G'=G-vx．由 G 極小性知，G'有無圈 k-邊染色 c，染色集 C={1，2，…，k}．

1)若 c(xx1)?C(v)，則用 a7∈C(C(v)∪{c(xx1)})染 vx．因|C(C(v)∪{c(xx1)})|≥k-4≥1，故這樣的顏色a7存在，且染色c仍是無圈的．

2)c(xx1)∈C(v)，不妨設 c(vy)=1，c(vw)=2，c(uv)=3，A4=C{1，2，3}．考慮到 u，w 的對稱性，故只需考慮以下2種情形：

①若 c(xx1)=1，則用 a8∈C(C(v)∪{c(yy1)})染 vx．因|C(C(v)∪{c(yy1)})|≥k-4≥1，故這樣的顏色a8存在，且染色c仍是無圈的．

②c(xx1)=2．若存在a9∈C(C(v)∪C(w))，則用a9染vx．否則，可斷言對于A4中的任一個顏色i都有x1到w的(2，i)-雙色路，故A4?C(w)∩C(x1)．進一步，若1?C(x1)，則用1改染 xx1，轉至情形①．若1∈C(x1)，C(x1)=C{3}，則可假設對于A4中的任一個顏色i都有x1到u的(3，i)-雙色路，故A4?C(u)∩C(x1)．考慮uw邊的染色情況，可分以下2種情況加以討論：

i)當c(uw)=1時，C(w)=C{3}，C(u)=C{2}，可斷言 x1到 w 和 x1到 u無(2，1)-雙色路．此時，可用 C({1，2，3}∪{c(yy1)})中的某一色改染 vy，再用1染 vx．

ii)當 c(uw)∈A4時，C(w)=C{1}，C(u)=C{1}，可斷言 x1到 w 和 x1到 u 無(2，1)-雙色路．此時，可用C({1，2，3}∪{c(yy1)})中的某一色改染vy，再用1染vx，從而可得G的一個無圈k-邊染色，與G的極小性矛盾．所以，v不會關聯3-面．引理4證畢．

引理5 在3-面的邊界上沒有2個3-點相鄰．

證明 假設一個3-點u與一個3-點v相鄰在一個3-面uvw的邊界上．設u1≠w，v1≠w分別是u，v的另一鄰點，G'=G-uv．由 G 的極小性知，G'有無圈 k-邊染色 c，染色集 C={1，2，…，k}，設 c(uu1)=1，c(uw)=2．

1)|C(u)∩C(v)|=0．不妨設 c(vw)=3，c(vv1)=4．

①若 Δ≥4，則用a10∈C(C(u)∪C(v))染 uv．因 |C(C(u)∪C(v))|≥k-4≥1，故這樣的顏色a10存在，且染色c仍是無圈的．

②下設 Δ =3，w1是 w 的另一鄰點，染色集 C={1，2，3，4}．若3?C(u1)，則用3 改染 uu1，再用1 染uv;若2?C(v1)，則用2改染vv1，再用4 染uv．設3∈C(u1)，2∈C(v1)．考慮到c(ww1)的對稱性，不妨設c(ww1)=1．若 u1到 w1無(1，4)-雙色路，則用4 改染 uw，再用 2 染 uv．否則，設 u1到 w1有(1，4)-雙色路，且 4∈C(u1)，4∈C(w1)，C(u1)=C{2}．此時，用 4 改染 uw，2 改染 uu1，再用1 染 uv．

2)|C(u)∩C(v)|=1．

①c(uu1)=c(vw)或c(vv1)=c(uw)．由于這2種情況的證明過程相同，故不妨設c(uu1)=c(vw)=1，c(vv1)=3，A5=C{1，2，3}．可斷言對于 A5中的任一個顏色 i都有 u1到 w 的(1，i)-雙色路，故 A5?C(w)∩C(u1)，且 C(w)=C{3}．若 u1到 v1無(1，3)-雙色路，則用3 改染 uw，再用2 染 uv．否則，設 u1到 v1有(1，3)-雙色路，且3∈C(u1)，C(u1)=C{2}，1∈C(v1)．又若 A5C(v1)≠?，不妨設 4?C(v1)，則用4改染vv1，再用3染uv．所以設A5?C(v1)=C{2}．此時，用2改染vv1，再用3染uv．

②c(uu1)=c(vv1)．不妨設 c(uu1)=c(vv1)=1，c(vw)=3，A5=C{1，2，3}．可斷言對于 A5中的任一個顏色i都有u1到v1的(1，i)-雙色路，故A5?C(u1)∩C(v1)．若3?C(u1)，則用3改染uu1，轉化至情形①．因此，3∈C(u1)，C(u1)=C{2}．若2?C(v1)，則用 2 改染 vv1，轉化至情形①．因此，2∈C(v1)，C(v1)=C{3}．又若 A5C(w)≠?，不妨設4?C(w)，則用4改染 vw，再用3染 uv．所以下設 A5?C(w)=C{1}．此時，用3改染vv1，用1改染vw，再用4染 uv．

3)|C(u)∩C(v)|=2．若 c(uu1)=c(uw)，c(vv1)=c(vw)，不妨設 c(uu1)=c(uw)=1，c(vv1)=c(vw)=2，則用a11∈CC(w)染uv，從而可得G的一個無圈k-邊染色，與G的極小性矛盾．所以，在3-面的邊界上沒有2個3-點相鄰．引理5證畢．

引理6 若d(v)=5且v相鄰3個2-點，則v不與2-點關聯在一個3-面中．

證明 假設v與一個2-點u關聯在一個3-面uvw中．設x，y是與v相鄰的其他的2個2-點，z是v的另一個鄰點，x1，y1分別是2-點x，y的另一鄰點，G'=G-uv．由G 極小性知，G'有無圈k-邊染色c，染色集C={1，2，…，k}．若 c(uw)?C(v)，則用 a12∈C(C(v)∪{c(uw)})染 uv．否則，c(uw)∈C(v)，不妨設c(vx)=1，c(vy)=2，c(vz)=3，c(vw)=4．

1)若 c(uw)=1，則用 a13∈C(C(v)∪{c(xx1)})染 uv．2)若 c(uw)=2，則用 a14∈C(C(v)∪{c(yy1)})染 uv．3)c(uw)=3．因 d(w)≤Δ，故可記 C(w)中未出現的色為 c0，c0∈C{3，4}．當 c0=1時，用1改染uw，轉至情形1);當c0=2時，用2改染uw，轉至情形2);當c0∈CC(v)時，直接將c0染uv，從而可得G的一個無圈k-邊染色，與G的極小性矛盾．所以，v不與2-點關聯在一個3-面中．引理6證畢．

2 定理1的證明

設圖G是滿足定理1條件的一個邊數極小反例．以下將運用Discharging方法導出完成定理1證明所需要的矛盾．

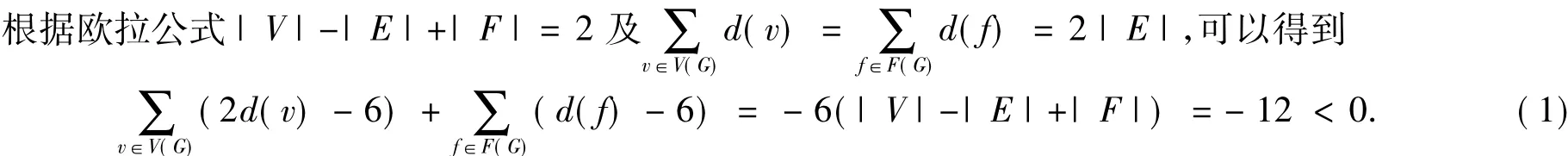
對任意 x∈V(G)∪F(G)，構造一個權函數 ω(x)．其中：當 v∈V(G)時，ω(v)=2d(v)-6;當 f∈F(G)時，ω(f)=d(f)-6．通過權轉移，得到一個新的權函數ω'(x)，使得總的權和不變．但對任意的x∈V(G)∪F(G)，有ω'(x)≥0．因此得到-12≥0，即得到了證明定理1所需要的矛盾．．

設v∈V(G)，n2(v)表示與點v相鄰的2-點個數，f3(v)表示點v關聯的3-面個數．

權轉移規則如下：

首先驗證 ω'(v)≥0，v∈V(G)．

情形1 v為2-點．由引理1和(R1)知，ω'(v)=2×2-6+1×2=0．

情形2 v為3-點．由權轉移規則知v既不轉出權也不接受權，故ω'(v)=2×3-6=0．

其次驗證 ω'(f)≥0，f∈F(G)．

［1］Fiamcˇík I．The acyclic chromatic class of a graph［J］．Math Slovaca，1978，28(3)：139-145．

［2］Alon N，McDiarmid C，Reed B．Acyclic coloring of graphs［J］．Random Structures Algorithms，1991，2(3)：277-288．

［3］Molloy M，Reed B．Further algorithmic aspects of Lovász local lemma［C］//Proceedings of the 30th Annual ACM Symposium on Theory of Computing held in Dallas．Dallas：ACM，1998：524-529．

［4］Muthu R，Narayanan N，Subramanian C R．Improved bounds on acyclic edge coloring［J］．Discrete Math，2007，307(23)：3063-3069．

［5］Alon N，Sudakov B，Zaks A．Acyclic edge colorings of graphs［J］．Graph Theory，2001，37(3)：157-167．

［6］Alon N，Zaks A．Algorithmic aspects of acyclic edge coloring［J］．Algorithmica，2002，32(4)：611-614．

［7］Cohen N，Havet F，Müller T．Acyclic edge-colouring of planar graphs，Extended abstract［J］．Eletronic Notes in Discrete Math，2009，34(5)：417-421．

［8］Sun Xiangyong，Wu Jianliang．Acyclic edge colorings of planar graphs without short cycles［C］//Proceedings of the 7th International Symposium on Operations Research and Its Applications held in Lijiang．Lijiang：APORC＆CAS，2008：325-329．

［9］Hou Jianfeng，Liu Guizhen，Wu Jianliang．Acyclic edge coloring of planar graphs without small cycles［J］．Graphs andCombinatorics，2011：10．1007/s00373-011-1043-0．

［10］Gao Yunshu，Yu Dongxiao．Acyclic edge coloring of planar graphs without cycles of specific lengths［J］．Appl Math Comput，2011，37(2)：533-540．