組合導航中抑制自適應濾波發散的研究*
宋 杰,晉 帆
(昆明理工大學信息工程與自動化學院,昆明 650500)
0 引言
現代主要的導航系統有捷聯慣導系統(SINS)、衛星全球定位系統(GPS)、無線電導航和組合導航系統等。其中SINS有誤差積累的問題,而GPS的信號容易受到遮蔽和干擾。對于高速運動和長時間飛行的載體,用單一的導航系統,很難達到理想的導航精度。為了提高導航的精度,采用將幾種導航系統組合起來,能有效提高導航的精度,更好的滿足載體對導航系統的要求[1-2]。
在組合導航系統中,如何將數據進行有效的融合成為一個關鍵問題。常用的方法是卡爾曼濾波(Kalman filter,KF),卡爾曼濾波是一種最小方差估計的方法。比較常用的還有Sage-Husa自適應卡爾曼濾波,利用觀測數據進行濾波遞推的同時,通過時變噪聲估值器,實時估計和修正系統噪聲和量測噪聲的統計特性。Sage-Husa自適應卡爾曼濾波的濾波精度要優于卡爾曼濾波,但是Sage-Husa自適應卡爾曼濾波容易出現濾波發散,其中穩定性和收斂性不能完全保證。文中主要針對Sage-Husa自適應卡爾曼濾波的發散進行研究,采用一種改進的自適應卡爾曼濾波抑制濾波發散,并且通過與卡爾曼濾波器的比較來驗證濾波效果。
1 SINS/GPS組合導航原理
捷聯慣性導航系統(SINS)的核心是用計算機來實現的慣性平臺。SINS用捷聯陀螺儀測量的載體角速度解算姿態矩陣,從姿態矩陣的元素中提取載體的姿態和航向信息;并用姿態矩陣把加速度計的輸出從載體坐標系變換到導航坐標系,然后進行導航解算[1]。在SINS中,對于高速運行和長時間的飛行后,其積累誤差越來越大,使精度降低。在組合導航系統中,需要借助GPS的輸出來提高組合導航系統的精度。
在文中,導航坐標系采用東-北-天地理坐標系。在組合導航系統中,其組合方式是采用位置速度組合的方式,用GPS和SINS輸出的位置和速度信息的差值作為觀測量,經組合的濾波器估計慣性導航系統的誤差,然后對慣性導航系統進行校正。SINS/GPS組合導航系統的結構圖如圖1。

圖1 SINS/GPS組合導航系統的結構圖
2 抑制濾波發散
2.1 常規卡爾曼濾波
組合導航系統離散數學模型的狀態方程和量測方程:

式中:Xk為k時刻的18維狀態向量,也是被估計向量;Zk為k時刻的6維量測向量;φk為k-1到 k時刻的系統一步轉移矩陣(18×18階);Wk-1為k-1時刻的系統噪聲;Гk-1為系統噪聲矩陣;Hk為k時刻的量測矩陣(6×18階);Vk為k時刻的6維量測噪聲。系統噪聲是不相關的高斯白噪聲。卡爾曼濾波是一種基于誤差方差最小準則的遞推線性最小方差估計算法,其離散卡爾曼濾波方程如式(2)~式(6):
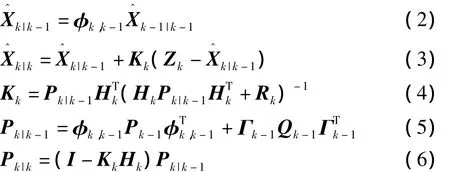
其中式(2)和式(5)是時間修正方程,其余3個方程是量測修正方程。式中:Rk和Qk分別稱為系統噪聲和量測噪聲的方差矩陣;Kk為濾波增益矩陣;Pk為估計均方差矩陣,而Pk|k-1為一步預測均方差誤差矩陣。
2.2 自適應Sage-Husa濾波算法的改進
自適應Sage-Husa濾波是在卡爾曼濾波算法的基礎上改進的一種算法,為了提高估計值的精度。在這種濾波方式中,Sage-Husa自適應卡爾曼濾波算法的濾波流程與卡爾曼濾波的方式是一樣的。只是在隨著濾波的遞推算法中,實時的估計系統噪聲和量測噪聲[2-3]。其中時變噪聲統計遞推估值器為:
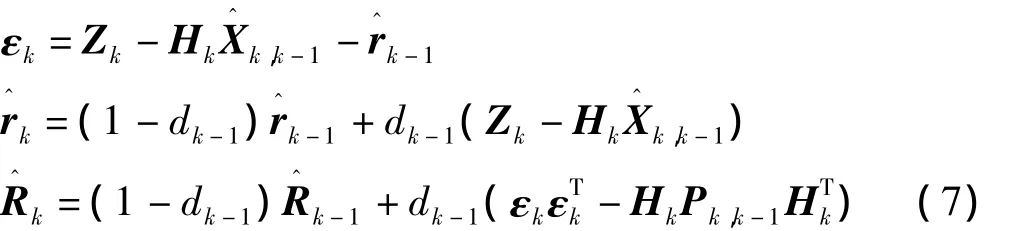

其中,dk-1=(1-b)/(1-bk),0<b<1為遺忘因子。通常取b的范圍為0.95<b<0.995。在對系統噪聲統計特性的計算過程中,由于系統噪聲和量測噪聲的方差矩陣在遞推的過程中,方差矩陣變得越來越大,造成Pk趨向無窮大,使得濾波發散,不能再修正系統噪聲和量測噪聲。
為了抑制濾波的發散,對自適應Sage-Husa濾波中的Rk和Qk進行改正來解決濾波發散的問題。改進濾波算法后,其時變噪聲統計遞推估值器變為:

改進后的自適應Sage-Husa算法是實時計算濾波過程中的系統噪聲和量測噪聲,然后用獲得的系統噪聲和量測噪聲求出當前時刻的系統噪聲和量測噪聲的方差矩陣,并通過與以前時刻的系統噪聲和量測噪聲的方差矩陣計算出總體的方差矩陣。這樣可以使得方差矩陣Rk和Qk比較穩定,使Pk變得越來越大,起不到修正的作用,造成濾波發散。
3 仿真結果與分析
文中仿真的過程中,慣性導航系統的陀螺隨機常數為 0.1°/h,隨機漂移均方差為0.1°/h,一階馬爾可夫噪聲驅動白噪聲均方差為0.1°/h,相關時間為200s;加速計一階馬爾可夫噪聲驅動白噪聲的方差為0.5m/s,相關時間為100s。GPS接收機隨機偽距測量誤差為50m,隨機偽距測量誤差為5m/s。初始位置為北緯30°、東經30°,海拔高度為1000m。飛行航跡在前100s內以90m/s的速度飛行,在后100s內以60m/s的速度飛行。
經過仿真之后得到的結果如圖2~圖6。
通過仿真結果圖可以看出在前20s內,改進后的自適應濾波器在各項導航參數的變化范圍比較大;如果采用自適應Sage-Husa濾波器的方法進行濾波,很容易造成濾波的發散。但是改進后的自適應濾波在后續的時間內沒有表現出發散現象。比較在經度、緯度和高度的位置誤差,可以明顯看出,改進后的自適應濾波器的濾波精度要高于卡爾曼濾波器,而且比較穩定。在東、北和天向速度的濾波過程中,在速度變化時刻第100s,可以看出自適應濾波在此時刻,東、北和天向速度都有明顯的變化,而在卡爾曼濾波器中則看不到這種變化,符合卡爾曼對方差總體的估計。
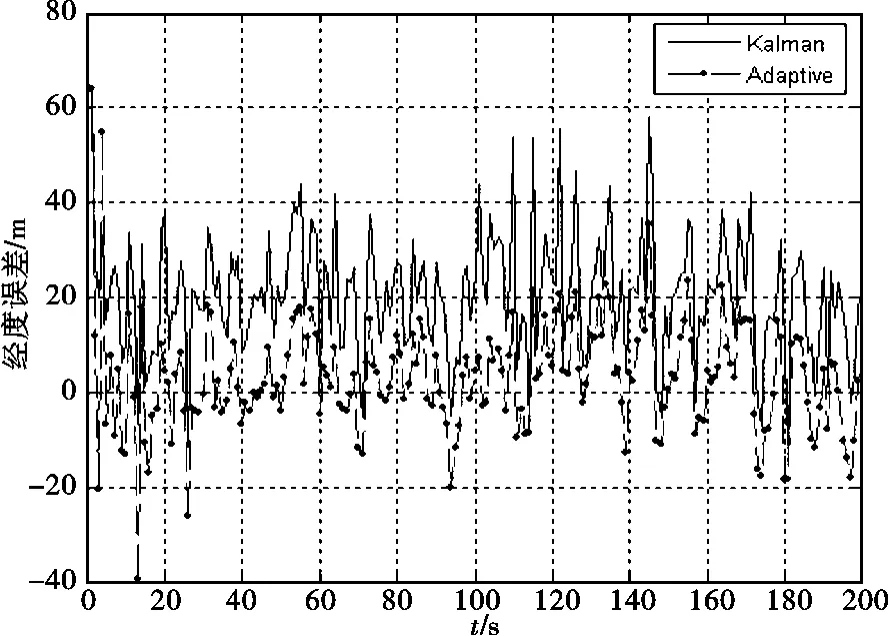
圖2 經度誤差曲線
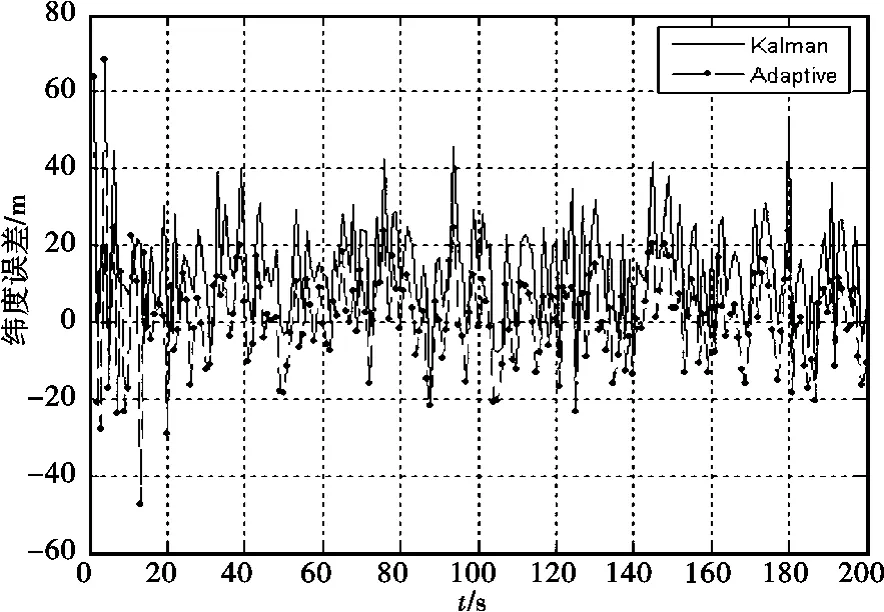
圖3 緯度誤差曲線
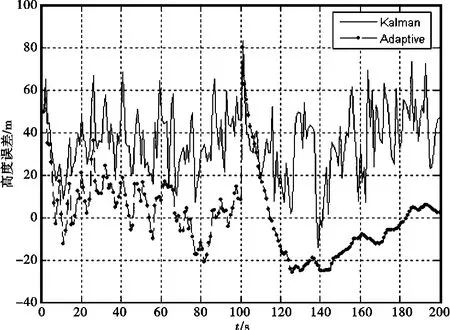
圖4 高度誤差曲線

圖5 東向速度誤差曲線
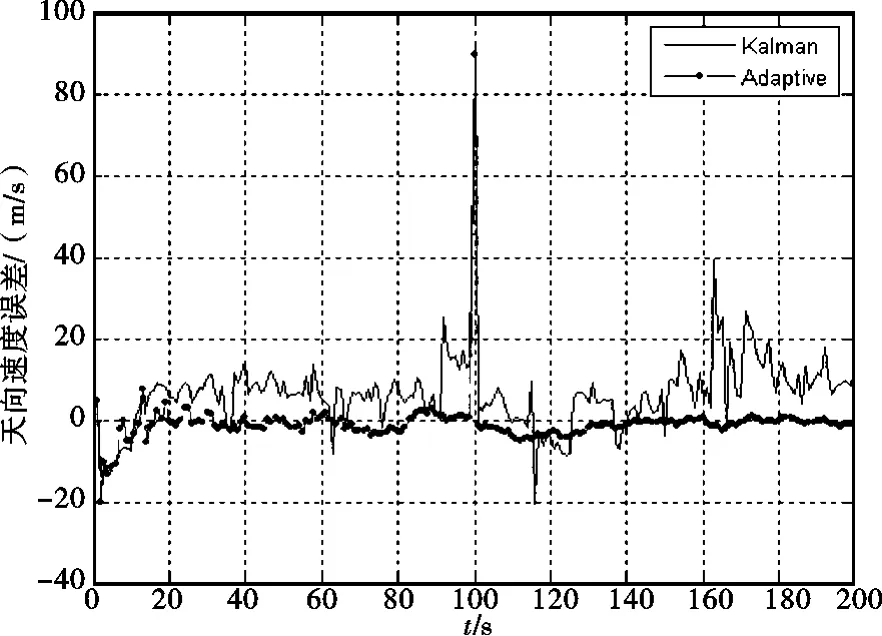
圖6 天向速度誤差曲線

圖7 天向速度誤差曲線
4 結論
通過以上的仿真實驗結果可以看出,經過改進的自適應Sage-Husa濾波器能夠避免濾波的發散,通過與卡爾曼濾波的比較,能夠獲得較高的精度和比較穩定的狀態。但是在狀態發生變化時,會引起各項導航參數精度的波動。
[1]劉建業,曾慶華,趙偉,等.導航系統理論與應用[M].西安:西北工業大學出版社,2010.
[2]趙俊梅.GPS/SINS組合導航系統濾波算法研究[D].太原:中北大學,2006.
[3]周媛媛.基于非線性模型的組合導航濾波算法研究[D].上海:上海交通大學,2008.
[4]宋迎春,陳正陽.GPS/INS組合導航中的自適應濾波算法[J].湘潭大學自然科學學報,2006,28(2):95-98.
[5]周愛軍,任光,郭模燦,等.一種新的自適應估計方法在組合導航系統中的應用[J].中國造船,2009,50(1):69-74.

