γ-矩陣構(gòu)成的3-李代數(shù)的結(jié)構(gòu)

白瑞蒲，周恒，李佳倩

（河北大學(xué) 數(shù)學(xué)與計算機(jī)學(xué)院，河北 保定 071002）

研究報告

γ-矩陣構(gòu)成的3-李代數(shù)的結(jié)構(gòu)

白瑞蒲，周恒，李佳倩

（河北大學(xué) 數(shù)學(xué)與計算機(jī)學(xué)院，河北 保定 071002）

γ-矩陣是物理上有重要應(yīng)用的矩陣，且γ-矩陣與3-李代數(shù)之間有著緊密的關(guān)系.證明γ-矩陣按照通常的換位運(yùn)算不構(gòu)成李代數(shù)，但γ-矩陣可構(gòu)成復(fù)數(shù)域上的單的3-李代數(shù).研究γ-矩陣構(gòu)成的3-李代數(shù)的結(jié)構(gòu)性質(zhì)、度量結(jié)構(gòu)及3-Hom李代數(shù)結(jié)構(gòu).

3-李代數(shù)；γ-矩陣；3-Hom-李代數(shù)；度量3-李代數(shù)

MSC 2010：15A69；17B05

n-李代數(shù)［1］的研究之所以受到越來越多的數(shù)學(xué)家及物理學(xué)家的關(guān)注，是因?yàn)槿藗儼l(fā)現(xiàn)多元李代數(shù)在很多領(lǐng)域都有著廣泛的應(yīng)用.特別是3-李代數(shù)的應(yīng)用更為廣泛.3-李代數(shù)被廣泛地應(yīng)用到幾何學(xué)、力學(xué)系統(tǒng)、弦論及 M2-膜理論［2-4］.例如，Bagger-Lambert理論的重要模型就是建立在度量3-李代數(shù)的結(jié)構(gòu)上.因?yàn)?Hom-代數(shù)理論與向量場的形變理論及微分計算有很密切的關(guān)系，Hom-李代數(shù)中的Jacobi等式利用線性映射進(jìn)行了扭轉(zhuǎn)，或是形變.所以在多元代數(shù)理論中也被廣泛的研究.

關(guān)于有限維n-李代數(shù)及n-Hom李代數(shù)的例子還很少，在文獻(xiàn)［5-6］中研究了特征零域上低維n-李代數(shù)的分類，及3-李代數(shù)的實(shí)現(xiàn)，為研究n-李代數(shù)的結(jié)構(gòu)提供了很多依據(jù).目前利用矩陣的基本運(yùn)算直接構(gòu)成n-李代數(shù)的實(shí)現(xiàn)問題及n-Hom李代數(shù)的實(shí)現(xiàn)，一直是人們在探討的問題.在數(shù)學(xué)物理中，γ-矩陣（γ1，γ2，γ3，γ4）也稱為Dirac矩陣，有著非常重要的應(yīng)用.γ-矩陣構(gòu)成了時間空間中反變向量的一組正交基的矩陣值表示，且γ-矩陣與3-李代數(shù)之間有著緊密的關(guān)系.本文利用γ-矩陣的乘積運(yùn)算構(gòu)造的3-李代數(shù)的結(jié)構(gòu)，且討論構(gòu)造的3-李代數(shù)的度量結(jié)構(gòu)及3-Hom李代數(shù)結(jié)構(gòu).本文假設(shè)所討論的代數(shù)是復(fù)數(shù)域上的代數(shù).首先介紹要用到的定義及符號.

3-李代數(shù) A是具有3-元運(yùn)算［，，］的域F上的線性空間，且滿足下列恒等式：?x1，x2，x3，y2，y3∈A，

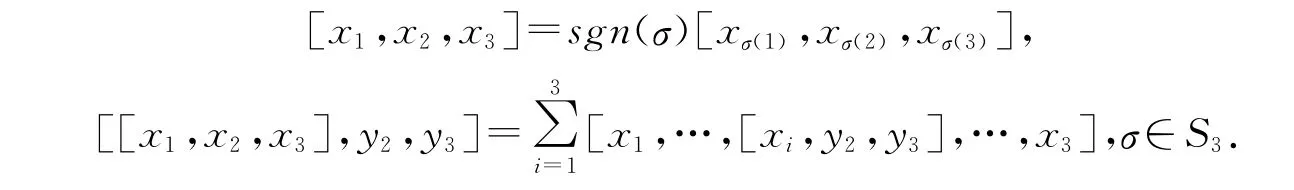
γ-矩陣γ1，γ2，γ3，γ4（也稱為Dirac矩陣）分別為：γ4＝diag（1，1，-1，-1），

記Λ為由γ1，γ2，γ3，γ4張成的復(fù)數(shù)域上的線性空間.直接計算可知，

從上面的計算可知，線性空間Λ按李代數(shù)的換位運(yùn)算不能構(gòu)成1個李代數(shù).

定義矩陣

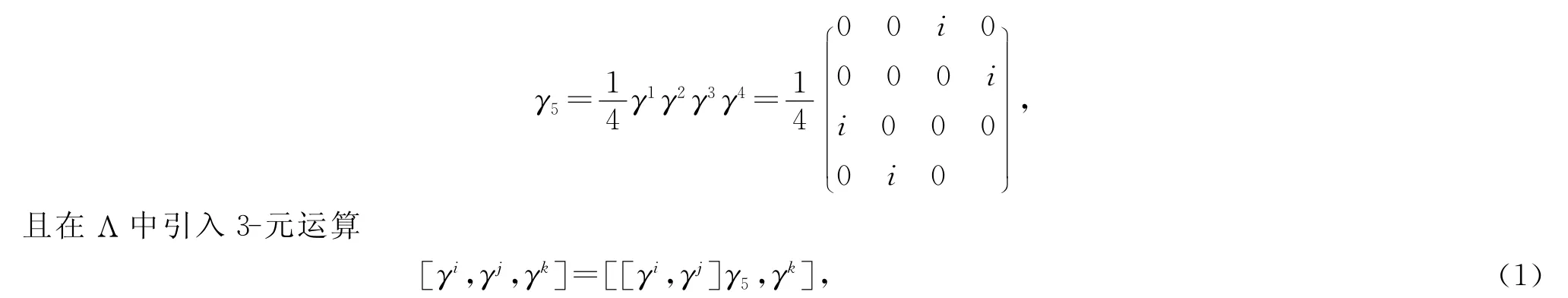
其中［γi，γj］＝γiγj-γjγi為換位運(yùn)算，則有下列定理.

定理1［6］線性空間Λ按運(yùn)算（1）構(gòu)成1個3-李代數(shù)，且具有乘法表

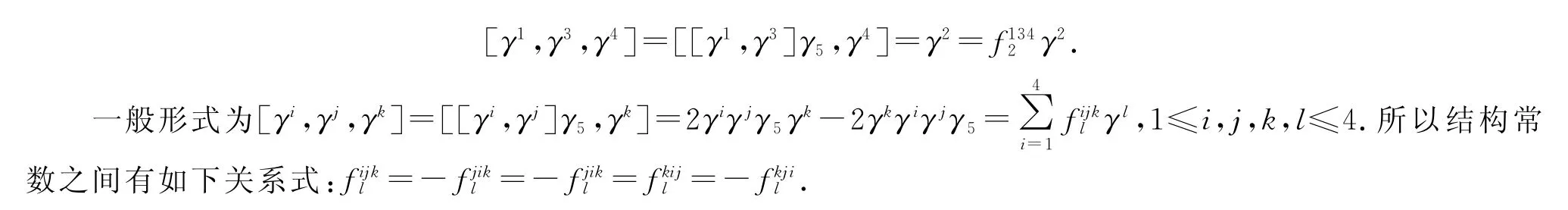
為進(jìn)一步研究3-李代數(shù)Λ的性質(zhì)，引進(jìn)下面的概念.

定義1 設(shè)L是域F上的3-李代數(shù)，μ：L?L→F是線性空間L上的非退化的對稱雙線性型，如果μ滿足

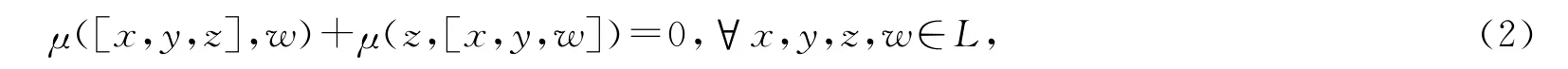
則稱μ是L上的一個度量，（L，μ）是度量3-李代數(shù).

3-李代數(shù)L上的雙線性型μ如果滿足等式（2），則稱μ是具有不變性的雙線性型.

定義2 設(shè)L是域F上的線性空間，［，，］：L∧L∧L→L是L的斜對稱的3-元線性運(yùn)算，α：L→L是線性變換滿足α（［x，y，z］）＝［α（x），α（y），α（z）］，?x，y，z∈L.如果α滿足對任意x，y，z，u，v∈L，有

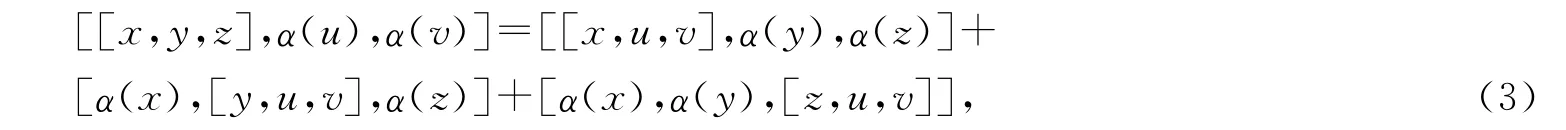
則稱（L，［，，］，α）為3-Hom-李代數(shù).如果α＝idL，則稱（L，［，，］，idL）是平凡的3-Hom-李代數(shù).

下面首先研究3-李代數(shù)Λ的度量結(jié)構(gòu).

定理2 設(shè)μ是由γ-矩陣構(gòu)成的3-李代數(shù)Λ的不變雙線性型，H＝（hij）是μ在基γ1，γ2，γ3，γ4下的度量矩陣，即hij＝μ（γi，γj）∈F，1≤i，j≤4.則hij滿足

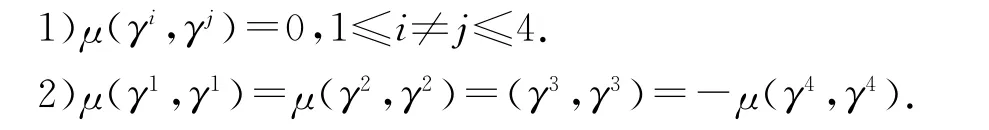
證明根據(jù)定理1及式（3），如果

綜合上述討論可得到μ的度量矩陣為H＝diag（λ，λ，λ，-λ），λ＝μ（γ1，γ1）.

推論由γ-矩陣構(gòu)成的3-李代數(shù)Λ上的對稱不變雙線性型μ非零的充要條件μ是Λ的一個度量，且在基γi，i＝1，2，3，4下的度量矩陣為diag（λ，λ，λ，-λ），λ∈F，λ≠0.

最后研究3-李代數(shù)Λ的Hom結(jié)構(gòu).

定理3 設(shè)Λ是由γ-矩陣按式（1）構(gòu)成的3-李代數(shù).α∶Λ→Λ是非零線性變換.則（Λ，［，，］，α）是-3-Hom-李代數(shù)的充要條件是α＝idΛ，即Λ按式（1）定義的3-元運(yùn)算構(gòu)成的3-Hom-李代數(shù)結(jié)構(gòu)僅有平凡結(jié)構(gòu).

證明由定理1可知，Λ的乘法表為：

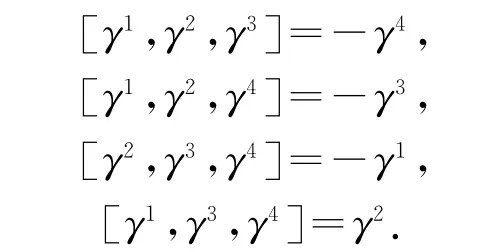
設(shè)α是3-李代數(shù)Λ的非零代數(shù)同態(tài)，且滿足式（3）.因?yàn)棣菃蔚?-李代數(shù)，所以α是3-李代數(shù)同構(gòu).因?yàn)棣淖酝瑯?gòu)群Aut（Λ）的李代數(shù)為Der（Λ）＝ad（Λ），所以Λ的代數(shù)同構(gòu)都為內(nèi)自同構(gòu).記：

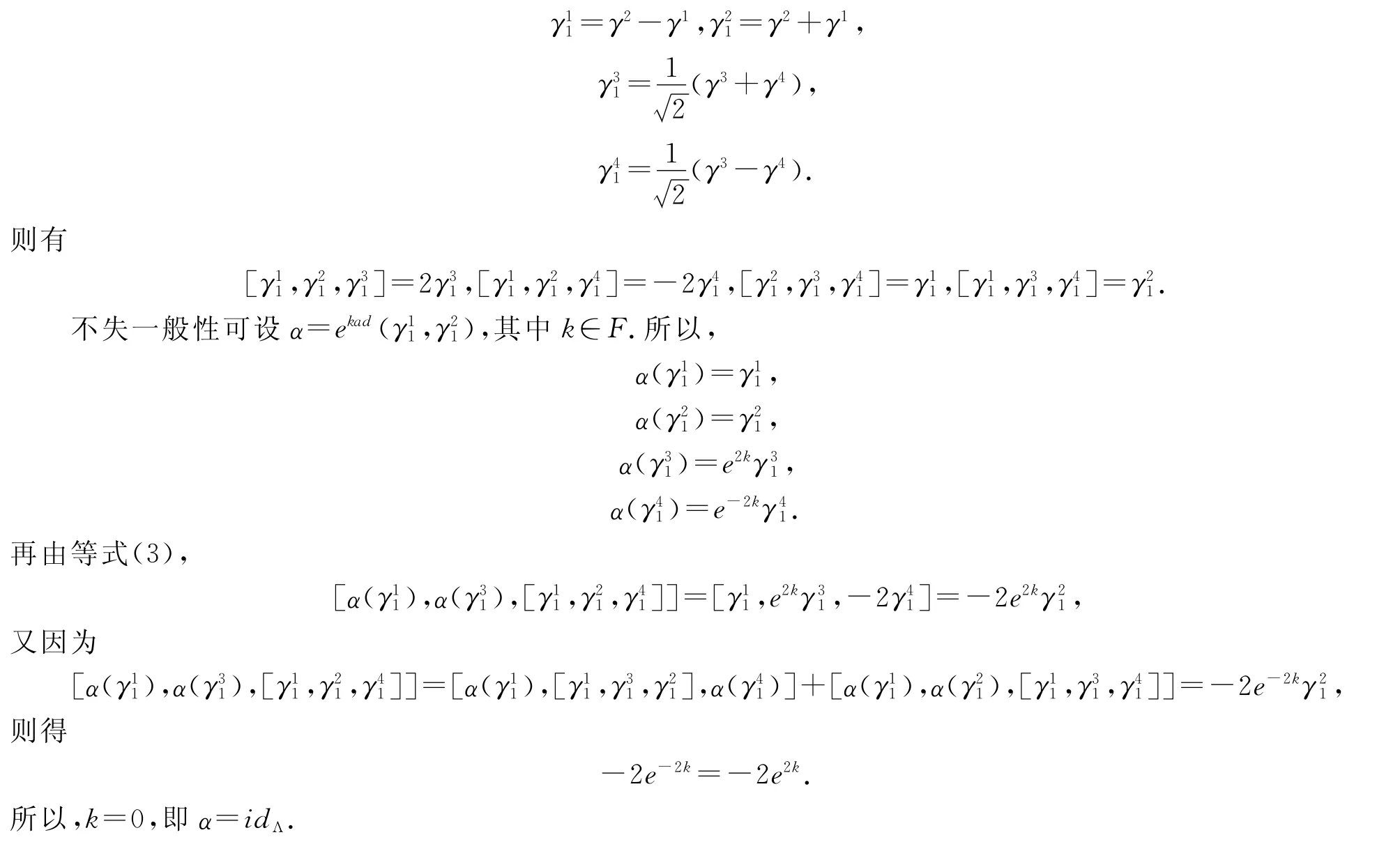
［1］ FILIPPOV V T.n-Lie algebras［J］.Sib Mat Zh，1985，26（6），126-140.

［2］ NAMBU Y.Generalized Hamiltonian dynamics［J］.Phys Rev D，1973（7）：2405-2412.

［3］ TAKHTAJAN L.On foundation of the generalized Nambu mechanics［J］.Comm Math Phys，1994（160）：295-315.

［4］ BAGGER J，N LAMBERT.Gauge symmetry and supersymmetry of multipleM2-branes［J］.Phys Rev D，2008（77）：065008.

［5］ LING Wuxue.On the structure ofn-Lie algebras［D］.Siegn：University-GHS-Siegn，1993.

［6］ BAI Ruipu，BAI Chengming，WANG Jinxiu.Relations of 3-Lie algebras［J］.J Math Phys，2010，51：063505.

［7］ 白瑞蒲，沈彩虹.一類低維可解3-李代數(shù)［J］.河北大學(xué)學(xué)報：自然科學(xué)版，2009，29（2）：126-128.

BAI Ruipu，SHEN Caihong.A class of solvable 3-Lie algebras of low dimension［J］.Journal of Hebei University：Natural Science Edition，2009，29（2）：126-128.

Structures of 3-Lie algebras generated byγ-matrices

BAI Ruipu，ZHOU Heng，LI Jiaqian
（College of Mathematics and Computer Science，Hebei University，Baoding 071002，China）

γ-matrix is impotant in physics，and it has close relaships with 3-ary algebras.The paper proved that the vector spaceΛofγ-matrices is non a Lie algebra in the multiplication defined by commutators.The simple 3-Lie algebra constructed on the vector space，metric structures and the Hom-structures are studied.

3-Lie algebra；γ-matrix；3-Hom-Lie algebra；metric 3-Lie algebra

O152.5

A

1000-1565（2012）05-0449-04

2012-03-27

國家自然科學(xué)基金資助項目（10871192）；河北省自然科學(xué)基金資助項目（A2010000194）

白瑞蒲（1960-），女，河北保定人，河北大學(xué)教授，博士，主要從事李群、李代數(shù)方面的研究.

E-mail：bairuipu＠hbu.cn

王蘭英）