塊修正插值技術在超聲波溫度場測量中的應用*

張華宇，謝鳳芹，李 強

(1.山東科技大學 機械電子工程學院，山東青島266590;2.兗礦集團股份有限公司濟三煤礦，山東濟寧273500)

0 引言

與常規的溫度測量方法相比，超聲測溫技術具有測量溫度原理簡單、非接觸、測溫范圍寬(0～1 900℃)、可在線測量等優點，現已廣泛應用于火箭、熔融液、汽缸氣體燃燒、核反應堆等處的測溫［1］。目前，大多數超聲測溫是基于對反射超聲進行分析或者是對超聲路徑上的平均溫度進行測量［2，3］。然而，在實際溫度測量過程中，燃燒過程具有瞬態變化、隨機湍流、環境惡劣等特點，如何獲得實際燃燒過程的熱物理量場參數是燃燒調整的可靠依據，其中溫度場的測量更加困難。因此，尋找一種簡單、快捷的方法進行溫度場的測量顯得尤為重要。本文利用聲波在媒質中的傳播速度的相關性為基礎，通過檢測聲速確定聲波在其中傳播的氣體溫度，建立了聲波在給定溫度場中傳播路徑的模型，在建立速度場的基礎上，對溫度場進行重建，并利用塊修正技術對重建結果進行修正。

1 超聲波測溫原理

超聲波測溫方法的基本原理是基于聲波在氣體介質中的傳播速度是該氣體組成成分和絕對溫度的函數［4］。在理想氣體下，聲波的傳播可以看成快速絕熱過程［5，6］，從而可得到其關系表達式為

式中 v為聲波的傳播速度，m/s;γ為氣體絕熱指數(等于定壓比熱容與定容比熱容之比);對于單原子氣體γ=1.67，對于雙原子氣體γ=1.40;三原子氣體γ=1.33。R為摩爾氣體常數，R=8.314J/(mol·K);M為氣體相對分子質量，kg/mol;T為氣體熱力學溫度，K。

如果γ，R，M已知，則通過檢測聲速就可確定聲波在其中傳播的氣體溫度，則式(1)可表示為

由于實際氣是混合氣體，所以，必須對上式進行修正。令Tc為超聲波傳播路徑上氣體介質的平均溫度(℃)，Z=，則由公式(2)可得

對于特定氣體，Z為常數。在實際的應用過程中，由于兩聲波接收器間的距離d是固定的已知常數，則可通過測定2只聲波接收器間聲波的渡越時間(time of flight，ToF)來確定聲波在傳播路徑上的平均溫度。

2 基于塊修正技術的溫度場重建

溫度場重建的算法有基于最小二乘法的重建算法、傅立葉正則化重建算法、基于雙線性模型的重建算法等多種方法。應用這些算法在實際的測量過程中，雖然能夠在某種程度上達到一定的測量精度，但是由于受傳感器布置和網格劃分個數的限制，在更復雜的環境中或精度要求更高的場合常常不能達到測量要求。而基于塊修正技術的溫度場重建法在傳感器布置狀況相同的情況下對溫度場的重建結果更加準確，能夠符合實際測量現場的參數，實際應用方法如下文所述。

假設在一個圓形的被測溫度場周圍均勻安裝n只超聲波發射/接收器，考慮到超聲波發射器的發射角最大不超過90°，每個超聲波發射/接收器發出的超聲波信號被其他接收器所接收，除了與發射器相鄰的2只接收器不能被接收，則共有k條聲波路徑。

聲波在任一條被測路徑上的渡越時間D可表示為

式中 s為路徑距離;D為聲波沿任一條聲波路徑上的渡越時間;a代表空間性質，其為聲速的倒數。

如果將被測溫度場劃分為N個小區間，將這N個區間從左至右，從上到下依次用數字i表示，i=1→N，每一個小區間的溫度是未知的并假定是均勻的，用Δski表示第k條路徑通過第i個小區間的長度，用ai表示超聲波穿過每個小區間的速度的倒數，則聲波沿第k條聲波路徑的渡越時間Dfly可表示為

通過上式可得超聲波通過每個小區間的平均速度，又有式(3)可得每個小區間的平均溫度，以該平均溫度作為對應小區間中心點的溫度，表示為Txy，如圖1所示。

假設Rx，y為溫度場x，y處的測量溫度值余量，則其絕對值的大小反映了溫度場收斂的程度，則Rx，y可表示為

圖1 塊修正插值技術中中心點的位置Fig 1 Position of center point in the block correction interpolation technology

式中 Tx，y為被測區域(x，y)方格處的中心點溫度，其他以此類推。ax，y，bx，y，cx，y，dx，y，ex，y為當前方格中心點溫度和相鄰方格中心點的溫度修正系數，fx，y為尾項修正系數。

在同一塊中各節點余量之和等于0，則Tx，y+代入同一塊中各節點的余量方程并對y求和

該式反映了在網格x這一豎塊上的整體能量守恒關系式，規定了修正值(x=2，3，…，Y1－1)上應滿足的條件，通過該代數方程組可確定。上式可進一步整理為

其中

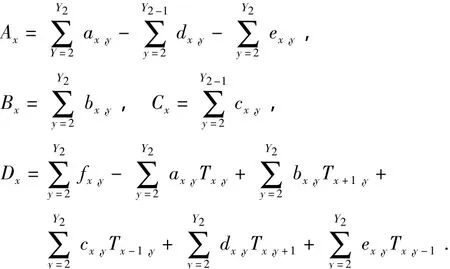
利用式(7)所給定的塊修正插值算法對每一個小方格中心點溫度進行修正，得到每一小區間的平均溫度，以每一個小區間的平均溫度作為對應小區間中心點的溫度進行二維插值，從而重建出整個測量區間的溫度場。

3 實驗與仿真

為了驗證上文所提到的溫度場重建算法，開發了基于虛擬儀器的聲學法溫度場測量裝置如圖2所示，該實驗裝置主要由超聲波收發器、調理電路、數據采集系統、數據采集總站、上位機以及LabVIEW數據采集軟件組成。該系統可控制8只超聲波換能器輪流發射超聲波，并對8只超聲波接收器采集的信號進行同步處理。將每一組超聲波發射/接收換能器按照順時針方向進行編號，分別為T/R1，T/R2，T/R3，…T/R8，每次只有一個發射器發射超聲波信號，當T/R1超聲波收發器發射信號時，對應得出7條路徑上的聲波渡越時間，分別讓T/R1到T/R8收發器依次發射超聲波信號，組成一個測量周期。溫度場測量系統在一個測量周期刷新一次溫度場顯示圖形，對被測量對象的溫度場進行重建。

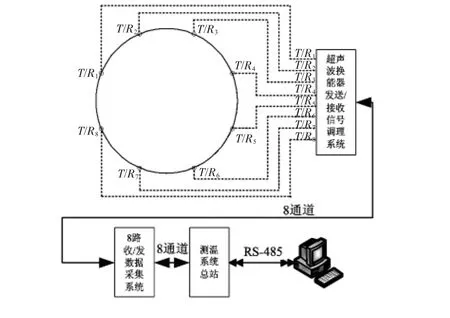
圖2 超聲波溫度場測試實驗裝置Fig 2 Experimental device for ultrasonic wave temperature field test

利用圖2所示的測量系統，對單熱源溫度場進行測量，單熱源采用電阻式加熱頭，熱電偶測量的溫度信息作為反饋，利用溫度控制器(韓國三元SU—105)控制溫度為170℃，熱源位置的相對坐標為(300，400 mm);溫度場測量區域為半徑是500 mm的圓形，采用8只傳感器對稱分布，考慮到超聲波傳感器的發射角限制，在實際測量時只能形成20條測量路徑，即每個傳感器只能形成5條路徑，將被測空間被均勻劃成10×10=100個區域，假定每個區域內的溫度分布是平均的，建立模型溫度場。在模擬計算時取每個區域的平均溫度為中心點的溫度值。

根據本文所述的塊修正插值建模理論，并對實際所測得的每條路徑上的超聲波渡越時間進行采集，結合修正技術重建溫度場，其二維溫度場重建結果如圖3所示;三維溫度場重建結果如圖4所示。

從圖3和圖4中可以看出:在(300，400 mm)的位置處，圓中心直徑1 cm范圍內，溫度為170℃，隨著直徑的擴大，外圍溫度(165，160，150，…，120℃)逐漸降低，并形成了各級溫度過渡的等溫線，符合實際被測量溫度場溫度分布情況。

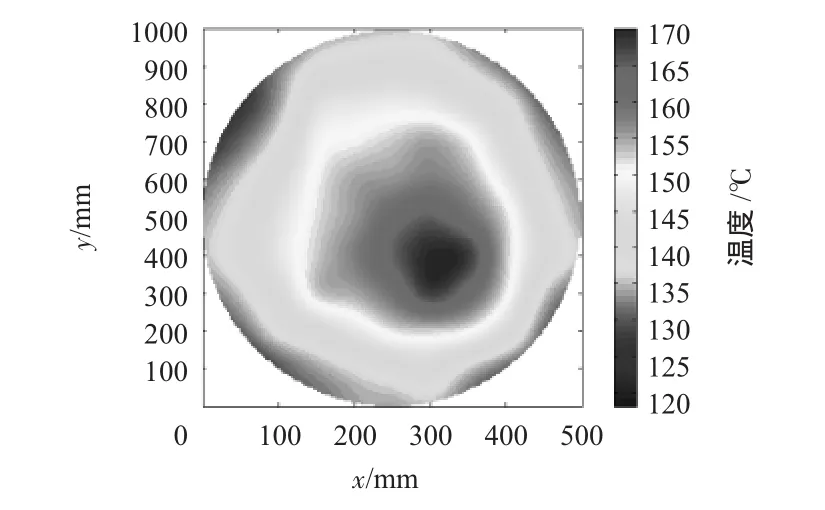
圖3 單熱源溫度場重建二維效果Fig 3 2D effect of single heat source temperature field reconstruction

圖4 單熱源溫度場重建三維效果Fig 4 Three-dimensional effect result of single heat source temperature field reconstruction

4 結論

在被測溫度場周圍布置8只收發一體的超聲波傳感器，并將被測溫度場劃分為100個小區間，利用超聲波通過每個小區間的平均速度，可得到每個小區間的平均溫度，亦即每個小區間的中心點溫度，以此為基礎，對整個網格上各個豎塊進行溫度值的細化和修正，并在此進行二維插值，從余量和計算源項上保證各小區間平均溫度計算的準確性。

基于塊修正插值技術的空氣溫度場重建方法只能在一個平面上的溫度場進行重建，對于不同平面上的溫度場無法使用該方法。在ToF的實際測量過程中，由于噪聲信號的影響和傳感器位置固定精度不夠等原因，導致溫度場中的等溫線并非標準圓形，所以，本實驗系統在精度方面還需要改善。

［1］范洪輝，朱洪錦，柳田裕隆，等.超聲波信號渡越時間參數法測量空氣中溫度分布［J］.應用聲學，2010，29(1):53－57.

［2］楊惠連，徐苓安.超聲相關流量計測量精度的探討［J］.儀器儀表學報，1993，14(1):90－95.

［3］葛萬成，吳鳳萍.兩步相關法高抗干擾超聲波距離測量技術的研究［J］.儀器儀表學報，2002，23(3):253－256.

［4］Tsai Wen-yuan，Huang Chih-feng，Liao Teh-lu .New implementation of high precision and instant-response air thermometer by ultrasonic sensors［J］.Sensors and Actuators，2005，117(4):88－94.

［5］Ohyama S，Takayama J.Temperature distribution and wind vector measurement using ultrasonic CT based on the time of flight detection［J］.Sensors and Actuators，2009，151(6):159－167.

［6］Wong G SK.Speed of sound in standard air［J］.Acoust，1986，79(3):1359－1366.