基于DSmT的機載目標斷續航跡關聯*

高 嵐，江 晶，藍江橋

(1.空軍雷達學院 研究生隊，湖北 武漢430019;2.空軍雷達學院四系，湖北武漢430019;3.空軍雷達學院，湖北武漢430019)

0 引言

機載平臺能夠搭載雷達、ESM等多種異類傳感器對目標進行探測。其中雷達等主動傳感器具有探測距離遠、精度較高，對目標的運動狀態信息掌握全面等優點，通常作為主傳感器完成對目標的跟蹤。然而其固有盲區、遮擋、雜波以及虛警等原因容易造成目標量測的斷續［1］，當目標再次被檢測到后將重新進行航跡起始，產生同一批目標出現多個批號并且短小航跡多等現象，即目標航跡斷續。在目標密集情況下，該問題將變得更加嚴重，給機載數據處理系統造成沉重負擔。因此，必須對中斷前后關于同一目標的航跡進行識別并合并，即進行斷續航跡關聯。

然而目標位置量測的不確定性及其可能進行的機動使得斷續條件下的關聯問題更加復雜。同時，ESM等機載被動傳感器能夠獲取目標的方位和屬性等多特征信息，并且抗雜波性能優良［2］，然而當目標的輻射源發生變化或者不可觀測時即無能為力。因此，機載雷達與ESM協同下的斷續航跡關聯是提高目標航跡連續性的有效途徑。

近年來，綜合利用目標多特征信息提高關聯準確性已經受到廣泛關注［3～7］。其關鍵問題在于如何度量各航跡配對的關聯度，不同的度量準則對應著多種關聯算法。主要的算法有模糊關聯［4］、神經網絡關聯［5］、灰關聯［6］以及 D-S關聯［7］等。其中基于D-S理論的關聯算法能夠處理多傳感器多特征量測的不確定問題，且適用條件更加靈活等優勢。然而其實際應用中存在對于沖突證據的合成效果差和潛在的計算量增大等問題［8］。本文提出一種基于DSmT［9］的斷續航跡關聯算法，該法通過建立中斷前后航跡段配對的關聯統計量，利用機載雷達與ESM的多特征量測計算相應關聯度并將其作為證據進行融合，最后通過設定閾值判斷中斷前后的航跡段是否關聯。

1 斷續航跡關聯問題

假設機載多傳感器(雷達、ESM等)對空中多目標進行觀測，采用分布式結構進行融合，各節點傳感器獲取目標量測數據后即完成本節點的數據配準與本地航跡起始。設融合中心k時刻已經形成關于目標j的穩定航跡，并且完成了節點間的航跡關聯;因此，融合中心得到的目標航跡已具有屬性信息。

根據多傳感器的位置融合結果，初始階段關于某目標的狀態估計為該目標航跡的最后更新時刻，M為目標航跡數，則該類航跡集合記為若由于檢測盲區、遮擋、低檢測概率條件下的大幅機動等因素造成的目標量測中斷時間較長，根據常規終止規則，目標航跡將出現斷續;一定周期后，經過同樣的起始關聯過程，融合中心重新得到了N條航跡，其對應目標的狀態估計記為為該目標航跡的起始時刻，該類航跡集合記為，如圖1所示。定義

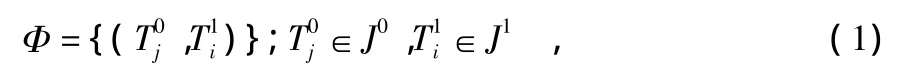
則Φ中的元素為所有可能的中斷前后航跡的組合，為了使目標航跡保持連續，必需確定其中正確的配對。對于多數非合作目標，其狀態的先驗知識是未知的，考慮到雜波、噪聲，以及分合批等問題，即使對于單目標情況，獲得令人滿意的正確關聯率仍是十分困難的。當目標密集且各目標航跡中斷的時間方位等有重疊的情況將更加復雜。

考慮到實際處理問題的方便，同時縮小判別范圍，可將中斷后航跡進行以下處理:對任意中斷后航跡T1i，利用與遞推濾波相似的思想，將其由航跡段末端向始端)進行逆向濾波，并繼續逆向外推至中斷前航跡的消亡時刻)，并根據反向預測波門判斷中斷前航跡是否與其相關。圖1給出了多目標航跡斷續關聯的典型情況。圖中的橢圓表示關聯波門，可以看到，由于沒有有效量測的更新，中斷后航跡T11，T12狀態反向預測的不確定性不斷增加導致波門放大，當重新獲得目標航跡，進行相關判斷的結果為T01，T02與T03均與T12航跡相關，同時T01與T03均與T11相關。顯然，該判斷結果還有待進一步確認。

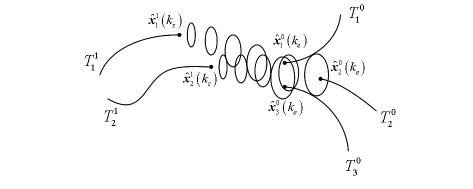
圖1 中斷前后的航跡段關聯示意圖Fig 1 Association of track segments before and after the broken off

2 多特征的基本信度分配

2.1 識別框架定義

對于中斷前后均為多目標情況，式(1)所描述問題的常用解決方法為多假設或多維分配法，然而其求解十分復雜。當N≥3時，N維分配問題為NP-hard問題，難以獲得其唯一解［10］。然而本文將DSmT引入多目標斷續關聯問題中，利用目標航跡中斷前后的多特征信息為依據，試圖尋找既便于求解又能獲得可靠正確關聯率的新途徑。

對于如圖1所示，某關聯門內的中斷前航跡T0j，其在此航跡關聯問題中的身份可以劃分為:正確關聯或者誤關聯，據此將該問題的識別框架Θ定義為

其中，命題θ1表示該中斷前航跡T0j與生成此關聯門的中斷后航跡T1i為同一批目標，命題θ2表示二者非同一批目標。

2.2 基本信度分配

支持命題的各條證據通過基本概率賦值獲得，在本文背景下，可以用來獲得基本信度分配的目標多特征信息包括位置、速度、徑向速度與目標輻射源信息，它們對于各命題的支持程度不同，并且有可能產生錯誤的證據(例如:目標輻射源信息，當航跡中斷前后的輻射源性質發生變化，如波形頻率等調整時，該證據可能出現錯誤)。對于任意，下面介紹各證據基本信度分配的獲取方法。

1)位置信息

其中，估計誤差

其協方差

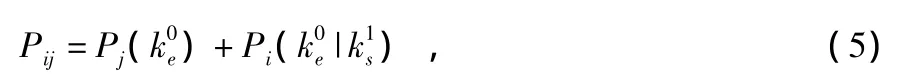
則dij為從自由度為n的χ2分布的母體中抽取的子樣，n為狀態估計的維數的子集。令

其中，Xs～χ2(n)，則稱ps為航跡中斷前后的目標位置的關聯度，將其作為根據位置信息獲得的支持命題θ1的基本信度分配m1(θ1)，支持命題θ2的基本信度分配m1(θ2)=1-ps，這里α為置信度。

2)速度信息

與(1)中的方法相似，取目標狀態向量中的速度分量建立相應的檢驗統計量，得到基于速度信息獲得的支持命題θ1的基本信度分配m2(θ1)=pv，支持命題θ2的基本信度分配 m2(θ2)=1-pv。

3)偽徑向速度

考慮由于徑向速度盲區導致的目標航跡斷續問題［3］(對于機載脈沖多普勒雷達而言，此原因導致的掉點現象十分常見)，由于目標落入機載脈沖多普勒雷達的徑向速度盲區造成的航跡中斷，中斷前后目標的偽徑向速度大小接近(都在門限附近)，則建立檢驗統計量

4)輻射源信息

雖然單個平臺上可能存在多個輻射源，但由于其用途不同會在頻率上產生較大差異，因此，選擇穩定且頻段固定的輻射源信息是可能的。對于輻射源的ESM信息，這里選用載頻(RF)、脈寬(PW)、重頻(PRF)等3個特征參數分別作為屬性向量。

設中斷前后目標載頻、脈寬、重頻均服從均值為零，噪聲標準差分別為σRF，σPW與σPRF的高斯分布。對中斷前后航跡段等間隔采樣l點，將ESM測得的目標航跡中斷前后的輻射源屬性信息視為從不同正態分布母體中抽取的子樣，則中斷前后采樣點的目標載頻、脈寬、重頻分別可表示為PF0(k)，RF1(k)，PW0(k)，PW1(k)，PRF0(k)與PRF1(k)。

這里建立各參數的檢驗統計量

若中斷前后航跡段屬于同一批目標，則tRFij為從服從自由度為l-1的雙尾t分布中抽取的子樣，令

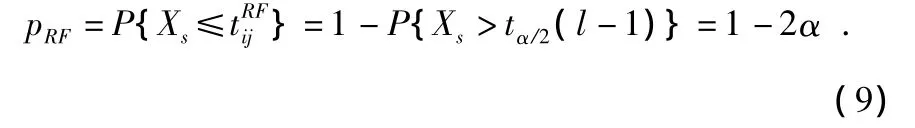
其中，Xs～t(l-1)。

稱pRF為航跡中斷前后的目標載頻信息的關聯度。同理可求得pPW與pPRF。由于3個特征相互獨立，因此，中斷前后的目標輻射源屬性關聯度可定義為:prad=pRFpPWpPRF，則基于輻射源信息獲得的基本信度分配 m4(θ1)=prad，m4(θ2)=1-prad。

3 沖突條件下的關聯規則

3.1 證據融合規則

PCR5規則是一種局部沖突局部分配的規則［11］，認為沖突信息的產生來自于辨識框架中有明確決策的單焦元之間沖突，并集產生的不確定信息不參與產生沖突，并且單焦元產生沖突的作用大小與其本身的信度值呈正比。于是，它將每次合成后產生的沖突信息按照單焦元的信度進行再分配，PCR5規則被定義為?(X≠Φ)∈GΘ。

當信息源數s=2時

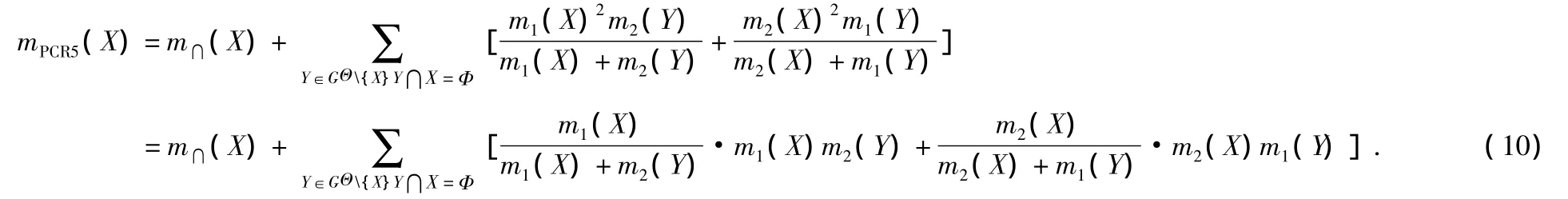
PCR5規則保持了空信度的合成后對結果的中立影響，得到的結果更加準確。在處理2個證據源的證據時，計算量適中，但處理3個或3個以上的信息源的證據時，計算量較大。因此，本文融合過程采取兩兩合成的方式。

3.2 實現步驟

1)根據中斷前后航跡段的數量確定待關聯的航跡配對集合Φ;

2)令i=1，j=1，將中斷后航跡 T1i逆向濾波并外推至最后更新時刻;

4)根據PCR5原則對各條證據進行兩兩合成得到新的證據 mij(θ1)與 mij(θ2);

5)j=j+1，回到步驟(2)，直到j=N;

6)設定不確定性合成信度閾值m0，當mij＞m0時判定識別過程有效，且可以作出決策:ans=max{m11(θq)，m12(θq)，…，m1j(θq)};

7)i=i+1，回到步驟(2)，直到i=M;

8)正確關聯結果輸出，其余未關聯航跡段判定為孤立航跡。

值得說明的是，決策過程中并未限制已經產生正確配對結果的航跡段參加下一輪分配，也就是說，該決策過程同時兼容了目標可能發生的分、合批情況。

4 仿真分析

假設兩平行目標相對于載機切向運動，由于落入機載雷達多普勒盲區，分別與雷達發現目標后的39，41 s量測丟失，由此目標航跡中斷;第55 s時同時發現三批目標并逐漸形成穩定航跡，如圖2所示。同時由機載ESM獲取的目標輻射源信息為(已完成與雷達航跡的關聯):目標1載頻}，脈寬0.5μs，重頻2kHz;目標2的載頻4000 MHz，脈寬1μs，重頻 8 kHz，目標 3 載頻為 5 000 MHz，脈寬0.8μs，重頻10 kHz;量測誤差標準差均為 σRF=5 MHz，σPW=0.02μs，σPRF=0.1 kHz。逆向濾波采用CV模型下的帶徑向速度的EKF進行。

由圖3可以看出:由于目標1，2近距飛行且在分批時進入盲區，因此，僅靠目標運動狀態信息進行相關判斷很容易出現模糊，例如:對于目標1，蒙特—卡洛仿真次數100，閾值為0.7時，根據目標位置、速度、偽徑向速度得出的證據得出的正確關聯率僅為40%;而加入輻射源信息后正確關聯率達到80%，且在另一方面，對于兩航跡段不屬于同一目標的正確識別概率達到100%，避免了航跡段之間的誤關聯。此結論同時也驗證了本文算法的可行性，在包括輻射源信息在內的有沖突的四條證據情況下，與沒有加入輻射源信息時相比已經能夠得出比較準確的結論。

在如圖1所示的多目標情況下，根據本文算法得出的基本信度分配見表1，可見各條證據間的沖突很大。通過PCR5法則進行合成后的結果見表2，由本文算法流程，可判別T01與T11相關，T02與T12相關，同時由于關于目標3的2個命題的識別結果均小于閾值，因此，將其判定為新目標。

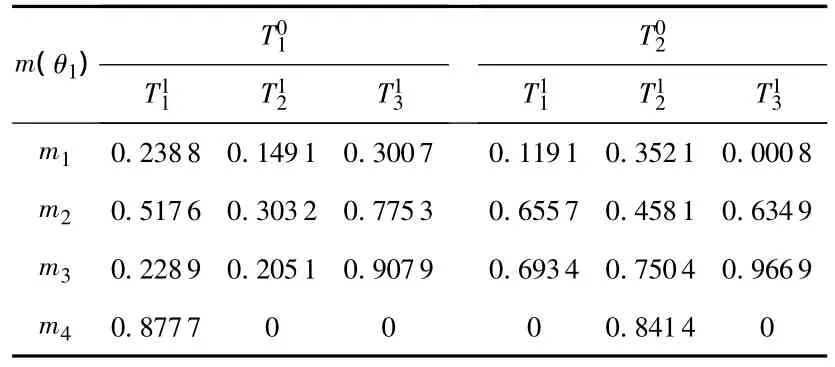
表1 各航跡段配對基本信度分配Tab 1 Basic belief distribution of every pair of track segments

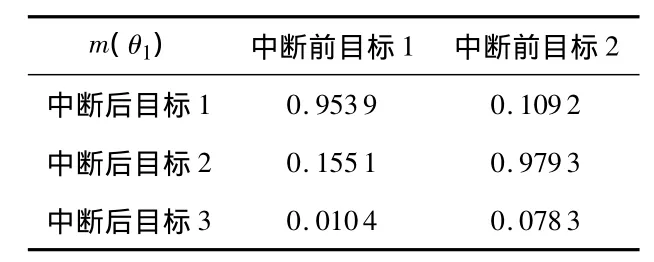
表2 識別結果Tab 2 Identification results

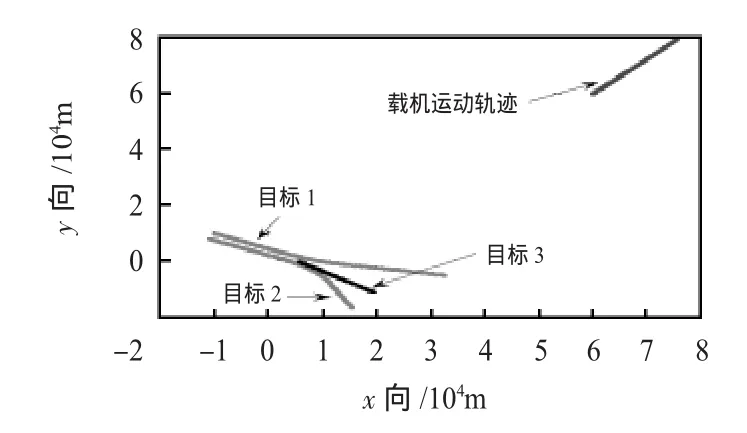
圖2 目標與載機的運動軌跡Fig 2 Moving tracks of targets and the airplane

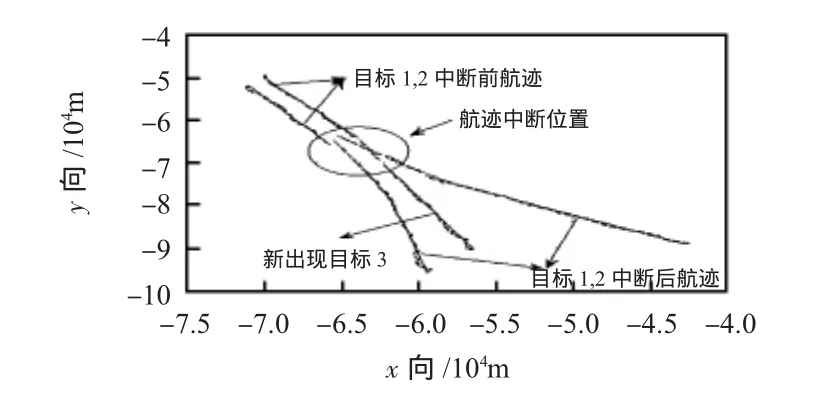
圖3 載機獲取的目標斷續航跡Fig 3 Target track segments obtained by the airplane

5 結束語

針對多目標航跡斷續問題，本文提出了基于DSmT的目標斷續航跡關聯算法。該算法首先將斷續后的航跡段進行反向預測，以確定有可能來自同一目標的中斷前航跡段。將可能來自于同一目標的中斷前后航跡段配對的關聯情況作為DSmT的識別框架，通過建立關聯統計量的方式，利用主被動傳感器獲取的位置、輻射源信息等目標多特征信息得到的關聯度作為各條證據的基本概率賦值，針對證據沖突的問題，利用PCR5規則將沖突再分配，減弱沖突對識別結果的影響，最后通過設定閾值進行關聯結果的判定。仿真結果證明該算法簡單易行，識別正確率高，同時對于一般方法不易識別的情況(例如:目標分合批等)具有適應性，對于工程實現具有指導意義。

［1］Morris G V.Airborne pulsed doppler radar［M］.London:Artech House，1988.

［2］何 友，修建娟，張晶煒，等.雷達數據處理與應用［M］.第二版.北京:電子工業出版社，2009.

［3］Bar-Shalom Yaakov，Kirubarajan T，Gokberk C.Tracking with classification-aided multiframe data association［J］.IEEE Trans on AES，2005，41(3):868-878.

［4］陸強強，章新華，郭徽東.一種利用目標屬性進行態勢關聯的方法［J］.火力與指揮控制，2007，32(9):84-87.

［5］Zaveri M，Merchant SN，Desai U B.Robust neural-network-based data association and multiple model-based tracking of multiple point targets［J］.IEEE Transactions on Systems，Man and Cybernetics，Part C:Applications and Reviews(S1094—6977)，2007，37(3):337-351.

［6］王杰貴，羅景青，靳學明.無源跟蹤中基于灰關聯信息融合的概率數據關聯算法［J］.電子學報，2006，34(3):391-395.

［7］Jiang Jing，Guo Jing，Luo Peng-fei，et al.Multisensor multipleattribute data association［C］∥CIE International Conference of Radar，Beijing，1996:393-396.

［8］Smets P.Data fusion in the transferable belief model［C］∥Proceedings of the 3rd International Conference on Information Fusion，Paris，2000:21-33.

［9］Dezert J.Foundations for a new theory of plausible and paradoxical reasoning［J］.Information and Security，2002，9:90-95.

［10］Zhou Li，Guan Jian，He You.Reseach of multi-dimension assignment algorithm of data association for passive-sensor location system［C］∥Proc of 2005 IEEE International Radar Conference，2005:133-136.

［11］Dezert J，Tchamova A，Smarandache F.Target type tracking with PCR5 and dempster’s rules—A comparative analysis［C］∥Proc of 2006 International Conference on Information Fusion，2006.