一種基于改進混合蛙跳的聚類算法*

韓曉慧，王聯國

(1.甘肅農業大學工學院，甘肅蘭州730070;2.甘肅農業大學信息科學技術學院，甘肅蘭州730070)

0 引言

聚類分析［1］作為數據挖掘在實際應用中的主要任務之一，是數據挖掘領域中一個很活躍的研究課題。近幾十年來得到了快速發展和成功應用。所謂聚類就是按照某個特定標準(一般為距離準則)把一個數據集分割成不同的類或簇，使得在類內的數據點的相似性盡可能大，同時類間的數據點的差異性也盡可能大［2］。

目前聚類算法主要分為:劃分聚類、層次聚類、基于網格的聚類和基于密度的聚類。K—均值算法作為劃分聚類中最經典的聚類算法之一，但它是一個局部搜索的算法，存在一些嚴重不足［3］:K值需要預先確定;聚類結果的好壞依賴于初始簇中心點的選取等。為此，許多研究者提出了基于智能優化算法的聚類方法［4～6］。

混合蛙跳算法作為智能算法的一種優化算法，是2000年由Eusuff和Lanse通過類比青蛙的覓食行為與優化問題求解的相似性而提出了一種新的基于全局協同搜索的智能優化方法。由于具有概念簡單、參數少、求解快速等諸多優點已被應用于許多自然科學與工程科學領域，顯示出強大的優勢和潛力。對求解實優化問題，大量實驗已證實，混合蛙跳算法較遺傳算法收斂速度快、效率高。鑒于此，本文在文獻［7］討論改進混合蛙跳算法的基礎上，提出了一種新的改進混合蛙跳的聚類算法，對算法進行了實驗分析，并與基于傳統混合蛙跳聚類算法、基于遺傳聚類算法和基于蟻群聚類算法進行了比較，仿真實驗證明本文提出的算法性能優于這幾種算法。

1 K—均值聚類算法

K—均值算法是一種基于劃分的方法，假設給定有n個對象的數據庫和聚類數目K。一個劃分方法構建數據的K個劃分(K≤n)，每一個劃分代表一個聚類。聚類依據對象之間的相似度函數，通常用距離來衡量，而距離度量的方式有很多，對于RN空間中的向量，最直觀的距離度量是向量之間的歐氏距離d=‖x－z‖。聚類的結果是達到類間的對象盡可能不同，類內的對象盡可能相似。

K均值聚類算法的過程描述如下:

輸入:數據集 X=(x1，x2，…，xn)，聚類數目 K

輸出:K個簇Cj

K—均值算法步驟描述如下:

1)從{x1，x2，…，xn}中隨機選取K個數據對作為初始簇(聚類)中心 z1，z2，…，zk;

2)計算每一個數據點xi，i=1，2，…，n與這K個簇中心Cj，j∈{1，2，…，k}的距離，如果滿足‖xi－zj‖＜‖xi－zm‖，m=1，2，…K，m≠j則 xi∈Cj

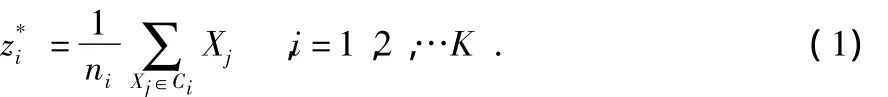
為防止不能滿足步驟(4)的終止條件出現無限循環，一般在算法執行時給一個固定最大迭代次數。

2 混合蛙跳算法

2.1 傳統混合蛙跳算法

混合蛙跳算法(SFLA)是一種受自然生物模仿啟示而產生的基于群體的協同搜索方法。在SFLA中，青蛙群體(解集)由一群具有相同結構的青蛙(解)組成，整個群體被分為多個子群，每個子群有自己的文化，執行局部搜索策略。子群中的青蛙均具有自己的思想，在局部搜索迭代次數結束之后，各個子群之間進行思想交流，實現子群間的混合運算。局部搜索和混合過程一直持續到定義的收斂條件結束為止，全局信息交換和局部深度搜索的平衡策略使得算法能夠跳出局部極值點，向著全局最優的方向進行［7］。

對于S維優化問題，SFLA算法首先從已知可行域中隨機生成P只青蛙組成初始群體，第i只青蛙表示問題的解為Xi=(xi1，xi2，…，xis)，計算每只青蛙的目標函數值f(Xi)，將每只青蛙根據其目標函數值按遞減順序排列，然后將整個青蛙群體劃分為m個子群，每個子群中包含n只青蛙。

對于每一個子群，目標函數值最好的解記為Xb和目標函數值最差的解記為Xc，而群體中目標函數值最好的解記為Xg。在每次迭代中，只對子群中的Xc進行更新操作，其更新策略為

其中，j=1，2，…，s，Dmax≥Dj≥－Dmax，Dj為分量 j上移動的距離，Dmax為青蛙的最大移動步長。

經過更新后如果得到的解newXc優于原來的解oldXc，則取代原來族群中的解。否則，則用Xg取代Xb重復執行更新策略

如果仍然沒有改進，則隨機產生一個新的解取代原來的Xc。重復這種更新操作，直到設定的迭代次數，當所有子群的局部深度搜索完成后，將所有族群的青蛙重新混合、排序和劃分族群，然后再進行局部深度搜索，如此反復直到達到事先設定的混合次數。

2.2 改進混合蛙跳算法

改進SFLA中，在文獻［7］的基礎上，提出了新的移動距離更新方式，每個族群進行局部深度搜索時，除了分量j上移動的距離引入上一次的移動距離，另外也加入了慣性權重系數，用來調節搜索能力。所以，式(2)變為

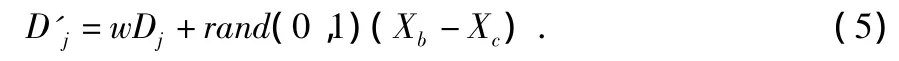
其中，w 為慣性權重系數，設置為0.9～0.4，D'j表示本次更新時分量j上移動的距離，Dj表示上次更新時分量j上移動的距離，群體初始化時，Dj以隨機方式產生。

經過更新后如果得到的解newXc優于oldXc，則取代原來族群中的解，否則，按下式計算移動距離

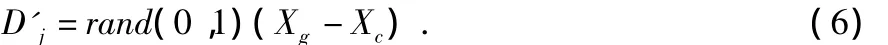
式(6)不包含上次移動距離，因為上次按式(5)更新后的解比原來的解更差，說明上次的移動距離不夠理想，所以式(6)消除了歷史不良影響，使得青蛙快速移動到全局最優解附近，從而可以加快收斂速度。如果newXc仍然沒有改進，則隨機產生一個新的解取代oldXc。改進SFLA中除了移動距離的計算方式與傳統SFLA不同外，其他操作都與傳統SFLA相同。

3 基于改進混合蛙跳的聚類算法

3.1 適應度函數設計

混合蛙跳算法在處理過程中以適應度函數為依據，利用種群中每個個體的適應度值來進行搜索。因此，影響混合蛙跳算法的收斂速度重要的是適應度函數的選取。對于每個個體，進行聚類的劃分和重新計算各聚類的中心采用與K—均值算法相同的方式，然后根據每個聚類中的點與相應聚類中心的距離和作為判斷聚類劃分質量的評價函數，E越小表示聚類劃分質量越好。

混合蛙跳算法的目的是搜索使評價函數最小的聚類中心，因此借助評價函數構造適應度函數如下

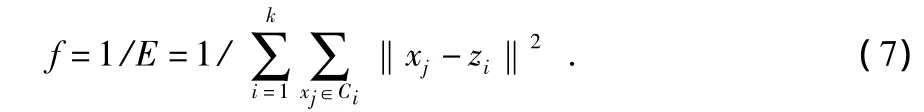
3.2 算法流程

本文提出的基于改進混合蛙跳的聚類算法流程如下:1)設定算法初始參數。

2)初始化種群和K個初始聚類中心。

3)對種群中的青蛙個體執行K-means操作。即，計算待分類集合{x1，x2，…，xn}到青蛙對應的K個中心的距離，根據距離將{x1，x2，…，xn}分類。

4)由分類計算出每只青蛙的適應度，按適應度大小對青蛙種群進行降序排列，隨機生成Dj。

5)將青蛙群體分成m個族群，每個族群包含n只青蛙，確定各個族群中的最優解Xb、最差解Xc以及全局最優解Xg。

6)按式(3)和式(5)更新最差解 Xc得到 newXc，對newXc進行約束處理，若newXc優于oldXc，則取代oldXc;否則，按式(3)和式(6)更新最差解Xc得到新的newXc，再對newXc進行約束處理。更新族群中的最優解和最差解，局部迭代次數加1，重復執行以上過程，直到達到設定的最大局部迭代次數，跳至步驟(7)。

7)將族群合并成一個青蛙群體重新按適應度函數值對青蛙群體進行降序排列，全局迭代次數加1，跳至步驟(5)。重復執行以上過程，直到達到設定的全局最大迭代次數，算法終止，輸出結果。

4 實驗結果

通過UCI數據庫中兩組實際數據集Crude oil和Iris數據集來驗證本文算法的性能。數據集信息概況如表1所示。

表1 Crude oil和Iris數據集的信息Tab 1 Information of Crude oil and Iris data set

為了能進一步驗證本文算法的性能測試，將本文算法與基于傳統混合蛙跳算法(SFLA)、基于遺傳算法(GA)和基于蟻群算法(ACO)［8～10］的聚類結果進行了比較，通過運行多次來比較算法的性能，如表2，表3。

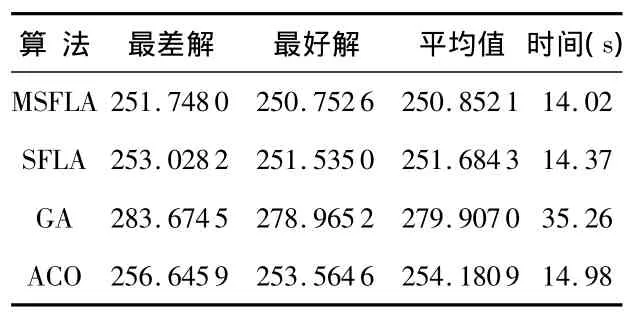
表2 四種算法對Crude oil聚類性能比較Tab 2 Comparison of Crude oil clustering characteristic by the four algorithms

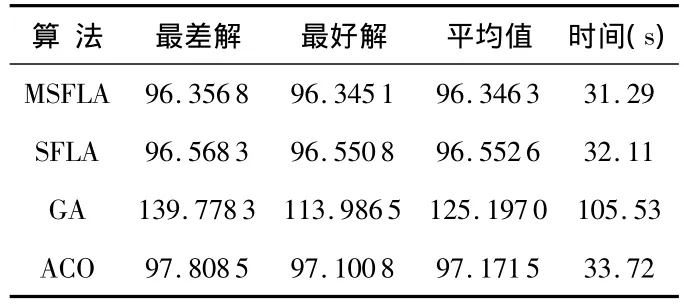
表3 四種算法對Iris聚類性能比較Tab 3 Comparison of Iris data clustering characteristic by the four algorithms

由以上表2、表3可以看出:基于改進混合蛙跳的聚類算法得到的結果，在收斂精度和速度上都能達到較好的聚類效果，優于基于傳統混合蛙跳算法、遺傳算法和蟻群算法的聚類方法。

5 結束語

K—均值聚類算法因其思想簡單而成為聚類分析最常用方法之一，但K—均值法分類的結果依賴于選擇的初始聚類中心，對于有些初始解K—均值法可能收斂于次優解。許多學者提出了基于智能優化算法的聚類方法來解決K—均值算法的這一缺陷。本文提出的基于改進混合蛙跳算法的聚類方法，引入了K—均值操作，提高了算法的局部搜索能力和收斂速度。實驗結果驗證了基于改進混合蛙跳算法的聚類方法的有效性和優越性。

［1］Jain A K，Murty M N，Flynn P J.Data clustering:A review［J］.ACM Computing Surveys，1999，31(3):264－323.

［2］楊小兵.聚類分析中若干關鍵技術的研究［D］.杭州:浙江大學，2005.

［3］Huang Z.Extensions to the K-means algorithm for clustering large data sets with categorical values［J］.Data Ming and Knowledge Discovery，1998(2):283－297.

［4］劉向東，沙秋夫，劉勇奎，等.基于粒子群優化算法的聚類分析［J］.計算機工程，2006，32(6):201－203.

［5］陸林花，王 波.一種改進的遺傳聚類算法［J］.計算機工程與應用，2007，43(21):170－172.

［6］劉 白，周永權.一種基于人工魚群的混合聚類算法［J］.計算機工程與應用，2008，44(18):136－138.

［7］鄭仕鏈，樓才義，楊小牛.基于改進混合蛙跳算法的認知無線電協作頻譜感知［J］.物理學報，2010，59(5):3612－3617.

［8］Amiri B，Fathian M，Maroosi A.Application of shuffled frogleaping algorithm on clustering［J］.International Journal of Advanced Manufacturing Technology，2009，45:199－209.

［9］Krishna K，Murty N.Genetic K-means algorithm［J］.IEEE Trans on SMC，1999，29:433－439.

［10］Shelokar P S，Jayaraman V K，Kulkarni B D.An ant colony approach for clustering［J］.Anal Chim Acta，2004，509:187－195.