眼科病床的設計進程調度方案

白城師范學院(137000) 張淑艷 鄔偉三 楊新宇

本文主要是通過建立合理的數學模型來解決該住院部的病床合理安排問題，以提高對醫院資源的有效利用。

問題的分析

排隊論(Queueing Theory)，又稱為隨機服務系統理論，是通過服務對象到來及服務時間的統計研究，得出這些數量指標(等待時間、排隊長度、忙期長短等)的統計規律，然后根據這些規律來改進服務系統的結構或重新組織被服務對象，使得服務系統既能滿足服務對象的需要，又能使機構的病人的安排指標最優。

排隊系統包括三個組成部分:

1．輸入過程。輸入過程考察的是顧客到達服務系統的規律。它可以用一定時間內顧客到達數或前后兩個顧客相繼到達的間隔時間來描述，本文為隨機型。由于患者到達醫院的時刻是隨機的，且在一定時間間隔［a，a+t］內，來醫院患者的概率與這段時間起始時刻無關，且與時刻a之前顧客數無關，在足夠小的時間內只有一顧客到達，并且到達患者有限，所以在［0，t］時，k個患者來到醫院的概率服從Possion分布，從而患者相繼到達的時間間隔t內必服從負指數分布，即在時間t內到達n個顧客的概率為

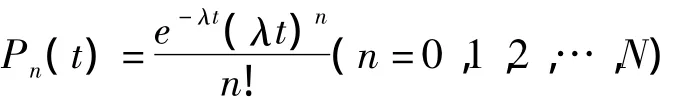
或相繼到達的顧客的間隔時間T服從負指數分布，即

式中λ為單位時間患者期望到達數，稱為平均到達率;1/λ為平均間隔時間。在排隊論中，討論的輸入過程主要是隨機型的。

2．排隊規則。分為等待制、損失制和混合制三種。當顧客到達時，所有服務機構都被占用，則顧客排隊等候，即為等待制。在等待制中，為顧客進行服務的次序可以是先到先服務，后到先服務，或是隨機服務和有優先權服務。如果顧客來到后看到服務機構沒有空閑立即離去，則為損失制。有些系統因留給顧客排隊等待的空間有限，因此，超過所能容納人數的顧客必須離開系統，這種排隊規則就是混合制。從本文提供的數據看為等待制。

3．服務機構。可以是一個或多個服務臺。本文屬于多個服務臺可以是并列排列的。服務時間一般也分成確定型和隨機型兩種。如果服從負指數分布，則其分布函數是 P{v≤t}=1 － e－μt(t≥0)式中μ為平均服務率，1/μ為平均服務時間。

ai(i=1，2，…，5)—各患者比例，i=1，2，…，5 分別代表白內障、白內障(雙眼)、青光眼、視網膜的患者;wi(i=1，2，…，5)—平均住院的時間;Di(i=1，2，…，5)—平均等待入院時間;wi+Di—各類患者的平均逗留時間。

為簡化問題，做出如下模型假設:

(1)假定顧客到達的時間間隔是相互獨立且同分布;(2)系統空間無限，允許白內障、青光眼、眼角膜疾病患者永遠排隊;(3)任意有限時間內到達有限個顧客的概率為1;(4)級別較高的比級別較低的顧客享有優先服務權;(5)外傷患者若在登記的第二日不能入院，則自動離開;(6)假設醫院眼科手術條件比較充分，沒有條件的限制;(7)每種疾病的手術時間都是相同的，即在一天內完成手術;(8)不考慮手術條件的限制。

因為病床始終沒有空閑時間，所以系統內平均逗留時間將是一常值。可將主要指標定為病床有效利用率和公平度。

為了討論方便分別稱白內障、白內障雙眼、青光眼、視網膜和外傷患者為第一類、第二類、第三類、第四類和第五類患者。

模型的初步建立和求解

1．排隊論M/M/C模型

來到醫院的患者服從泊松分布。對有s個服務臺的服務系統，需要用到如下公式:

其中S—服務機構中的服務臺的個數;Lq—系統中的平均排隊長度;Ws—顧客在系統中的逗留時間;Wq—顧客在系統中的平均等待時間;Ls—平均顧客人數;ρ—服務強度;τ—設備使用率;λ—平均到達率;μ—平均服務率;P0—系統的穩態概率。

結 果

(1)目前各個醫院考察病床的安排優劣，一般采用評價指標“病床使用率”。醫院病床使用率至少達90%以上才為合理使用該醫院眼科病床現使用率為56%，所以病床使用不合理，會導致等待住院病人隊列越來越長。且服務強度(有效到達率)ρ=0.0176，相對太低。

由已出院的數據知白內障、白內障(雙眼)、青光眼、視網膜患者的平均服務時間分別為5天、6天、8天和9天，所以在此排隊論系統中，將病人分為4個優先等級，第一優先級為白內障患者，第二優先級為白內障(雙眼)患者，第三優先級為青光眼患者，第四優先級為視網膜患者，同一天內到達的病人優先級高的病人先入住，第i級優先權的病人的到達服從參數為λi(i=1，2，3，4)的 Poisson 分布，同時，系統對任何級別病人的服務時間均服從參數為μ的負指數分布。

當患者的到達過程為參數λ的Poisson過程時，則患者相繼到達的時間間隔T必服從負指數分布，即每位患者接受服務的時間是獨立同分布的，其分布函數為 B(t)=1 －e－μt(t＞ =0)，其中 μ ＞0為一常數，代表單位時間的平均服務率，而1/μ則是平均服務時間。

用MATALAB軟件求解得p0=0.50945，平均到達人數Lq=5.64285，平均到達率λ=0.1547，平均服務時間wq=9.0086，平均服務率μ=0.111，服務強度ρ=0.0247.，隊長 L=7.0365，逗留時間 W=18，病床使用率τ=0.8019，易見病床使用率和服務強度都比醫院原來的安排模型要好很多。

(3)采用自適應區間法，計算出各類病人每日出院人數的統計平均值分別 1.309、1.491、0.709、1.836、1，而這五類患者相應的平均排隊時間為5.23、8.56、12.54、10.49、7.04 。為了讓患者以較高的可靠度得到大致的住院日期，取置信度為95%，對住院時間區間取整。則通過計算可得這5類患者的大致住院時間區間為［4，6］、［6，10］、［11，13］、［8，12］、［6，8］。

(4)白內障、白內障(雙眼)、青光眼、視網膜的患者從住院到手術的平均時間分別為3天、4天、3天、3天，周六，周日不安排手術，所以手術時間應作出相應調整，考慮到白內障(雙眼)需在一周內做完2次手術，其他眼科患者手術時間向后調整。由已有的各類患者的平均逗留時間可擬出剩余病人的入院時間和手術時間及出院時間。

(5)該問題為優化問題，由于病床數只能為整數，且數量較大，故采用分支定界法來建立模型。

由Lingo軟件計算可得各類病人占用病床的比例，其中白內障病人占17.72%;白內障(雙眼)病人占24.05%;青光眼病人占12.66%;視網膜病人占29.11%;外傷病人占16.46%。

白內障、白內障(雙眼)、青光眼、視網膜、外傷的患者在系統內的平均逗留時間(天)分別為16.15，18.07，20.7，22.08，8.036。

模型的評價和改進

該模型充分利用醫院數據，分析和研究了數據規律，實際地解決患者的滿意度情況，并且遵循公平原則、盡可能快的服務和盡可能擴大服務面等優點。

此模型存在一些不足之處:如模型的實際檢測不夠，而且在公平性方面還存在一些漏洞，因此，就這一點還有待于商榷。作為醫院，可以通過引進醫院叫號系統程序，來統計患者到達間隔和服務時間的經驗分布，然后按照統計學的方法進行檢驗，得出可靠結論。

1．王玉升．排隊論模型及其在醫院管理中的作用．中國醫院管理，1995，15(2):58．

2．石磊，賀正才．病床工作效率與經濟效益的關系分析．中國醫院統計，1998，3(1):37．

3．胡德奎，董軍，高筠．病人住院時間分布規律對住院日影響的研究．中華醫院管理，2000(6):362．

4．彭迎春，董斯彬，常文虎．運用排隊論模型測量醫院門診流程效率中國醫院管理雜志，2005，21(12);806-809．

5．梁國業．數學建模．北京:冶金工業出版社，2004．

6．徐玖平，胡知能，李軍．運籌學．北京:科學出版社，2008．

7．姜啟源，謝金星，葉俊．數學模型．北京:高等教育出版社，2003．

8．顧海．現代醫院管理學．中國醫藥科技出版社，2004．

9．崔雷．簡明醫學信息學教程．北京大學醫學出版社，2005．