基于線性回歸-馬爾可夫模型的鐵路客運量預測

李曉東

（沈陽鐵路局 沈陽客運段，遼寧 沈陽 110013）

我國經濟的快速發展、社會的進步改變了人們的工作方式和生活習慣，同時也改變了對運輸的需求。旅客的經濟能力和時間價值觀念逐漸增強，更加關注運輸質量，包括出行的便捷性、旅行的舒適性、旅行時間的縮短、安全性的提高、運輸服務水平等[1]。目前，鐵路運輸面臨著運輸數量和質量的雙重壓力。為解決鐵路運輸的“瓶頸”問題，我國進行了既有線提速和高速鐵路建設，預計 2012年投產新線 6 366 km。“十二五”期間，全國鐵路運營里程將達到12萬 km，其中以高速鐵路為主骨架的快速鐵路網達4.5萬 km，西部地區鐵路達 5萬 km。這將使鐵路既有的優勢得以充分發揮，同時也為鐵路的發展注入新的活力。

1 客運量預測模型的選擇

鐵路客運量既是衡量運營效果的一項重要指標，運輸部門可以根據客運量的變化及時調整戰略部署，同時也是鐵路項目可行性研究中的重點內容，是論證項目建設必要性和經濟性的基礎。國內外采用的鐵路客流量預測方法較多，其中定量預測方法可分為因果關系分析法、產運銷平衡法、四階段法等。這些方法在預測精度上都有待提高，以便為決策者提供更可靠的數據。在鐵路既有線提速前，客運量預測只是針對趨勢客運量。但是，既有線實施提速和高速鐵路建成投入運營，鐵路客運綜合服務質量得到提高，如果照搬某一種方法，預測結果將會出現偏差，并且隨著時間的推移，理論預測值和未來實際運量的誤差也會越來越大[2]。

回歸分析是一種應用極為廣泛的數量分析方法，主要用于確定2種或2種以上變量間相互依賴的定量關系。回歸分析的基本思想是：雖然自變量和因變量之間沒有嚴格的、確定性的函數關系，但可以設法找出最能代表它們之間關系的數學表達形式。因此，可以通過因變量和自變量來確定變量之間的因果關系，建立線性回歸模型，并根據實測數據求解模型的各個參數，然后評價回歸模型是否能夠很好地擬合實測數據，如果能夠很好地擬合，則可以根據自變量作進一步預測[3-4]。

線性回歸預測模型對經濟社會系統預測具有重要的意義，但由于客運量的影響因素復雜，其變化呈現一定的隨機波動特點，因而預測結果會產生誤差。而馬爾可夫鏈是根據系統狀態之間的轉移矩陣來描述一個隨機動態系統未來的發展狀態，轉移矩陣反映了各個狀態之間的規律性。馬爾可夫鏈過程最主要的特征就是無后效性，即t時刻之后的狀態只與 t時刻的狀態有關，而與以前的狀態無關。因此，可以通過對線性回歸預測模型的結果進行馬爾可夫鏈改進來提高其預測的準確性[5]。

2 鐵路客運量預測

2.1 線性回歸模型確定預測值

鐵路客運量的影響因素包括國民生產總值、人口數量、居民消費水平、運價、運輸服務水平、運輸方式結構等。目前，國家制定了“十二五”規劃，但以上因素仍存在一定的不確定性。因此，選取鐵路營業里程這一相對確定的指標進行線性回歸分析。2001—2010年我國鐵路客運量和鐵路營業里程如表1所示[6]。根據數據作散點圖，其趨勢大致呈線性關系，如圖1所示。

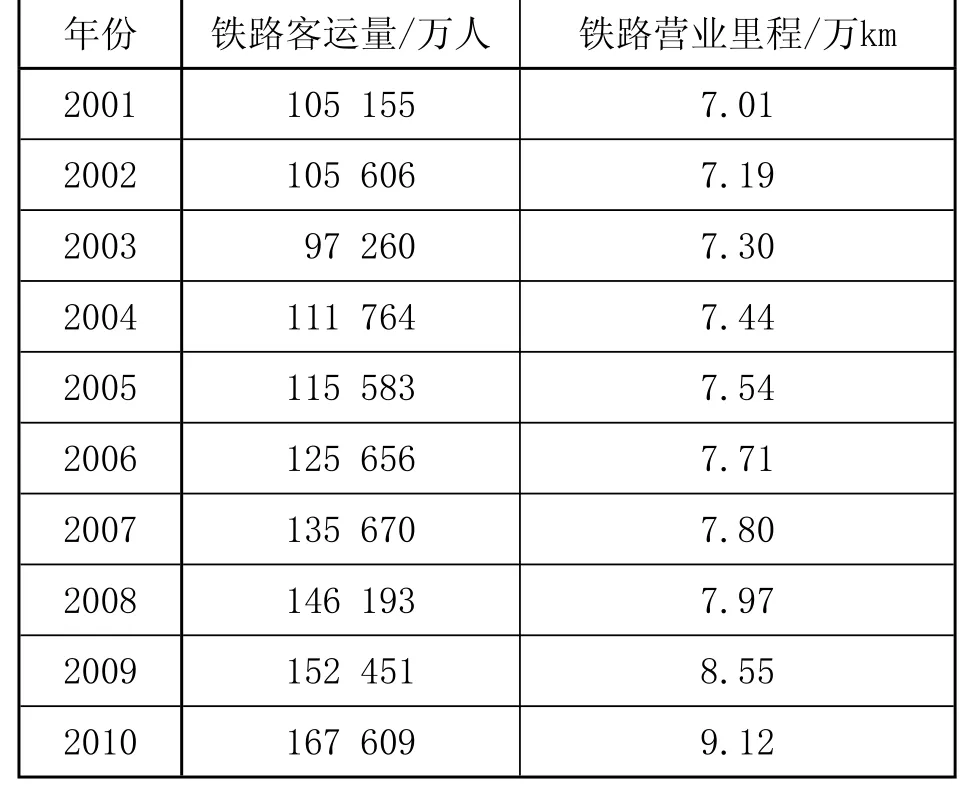
表1 2001—2010年全國鐵路客運量和鐵路營業里程

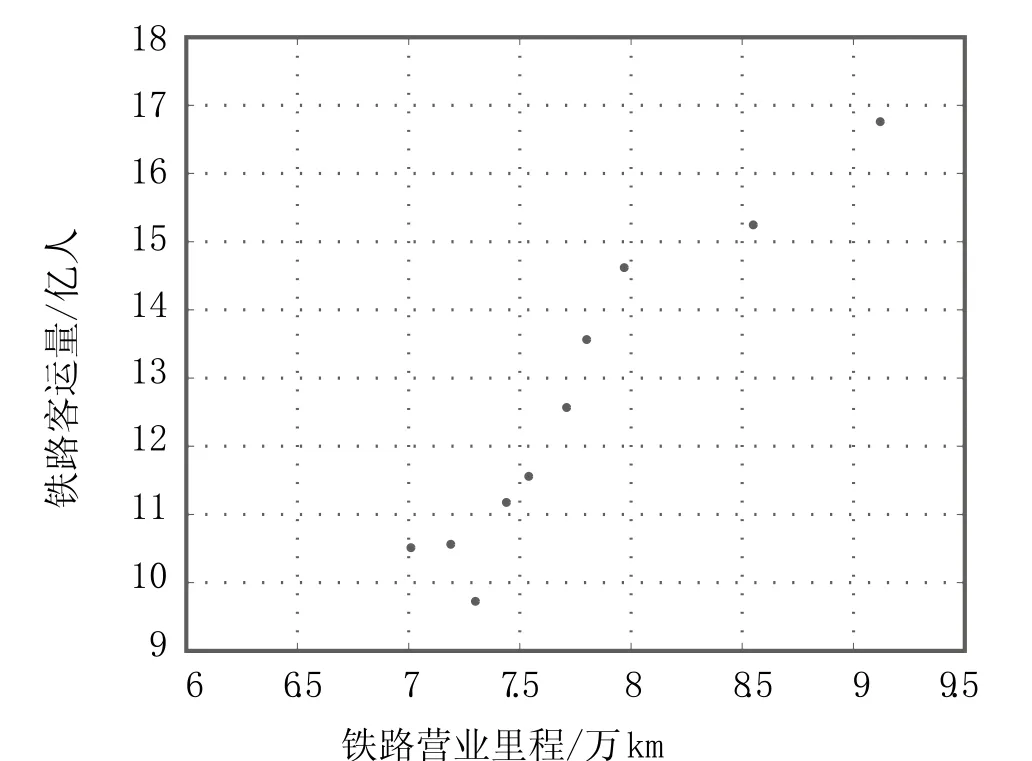
圖1 2001—2010年全國鐵路客運量和鐵路營業里程關系散點圖

按數據趨勢可以建立線性方程，應用 MATLAB 軟件，回歸方程為：

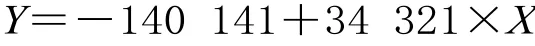
式中：X 為營業里程，萬km；Y 為鐵路客運量，萬人。

回歸模型擬合度檢驗結果顯示，相關系數為0.950，而決定系數 R2為0.903，回歸方程對樣本數據點擬合較好。

根據公布的數據：2011年鐵路新增線路 2 022 km，2012年計劃新增線路 6 366 km，2015年計劃鐵路線路全長達到 12萬 km。根據上述公式可以得到鐵路客運量的回歸預測值及相對誤差，如表2所示。

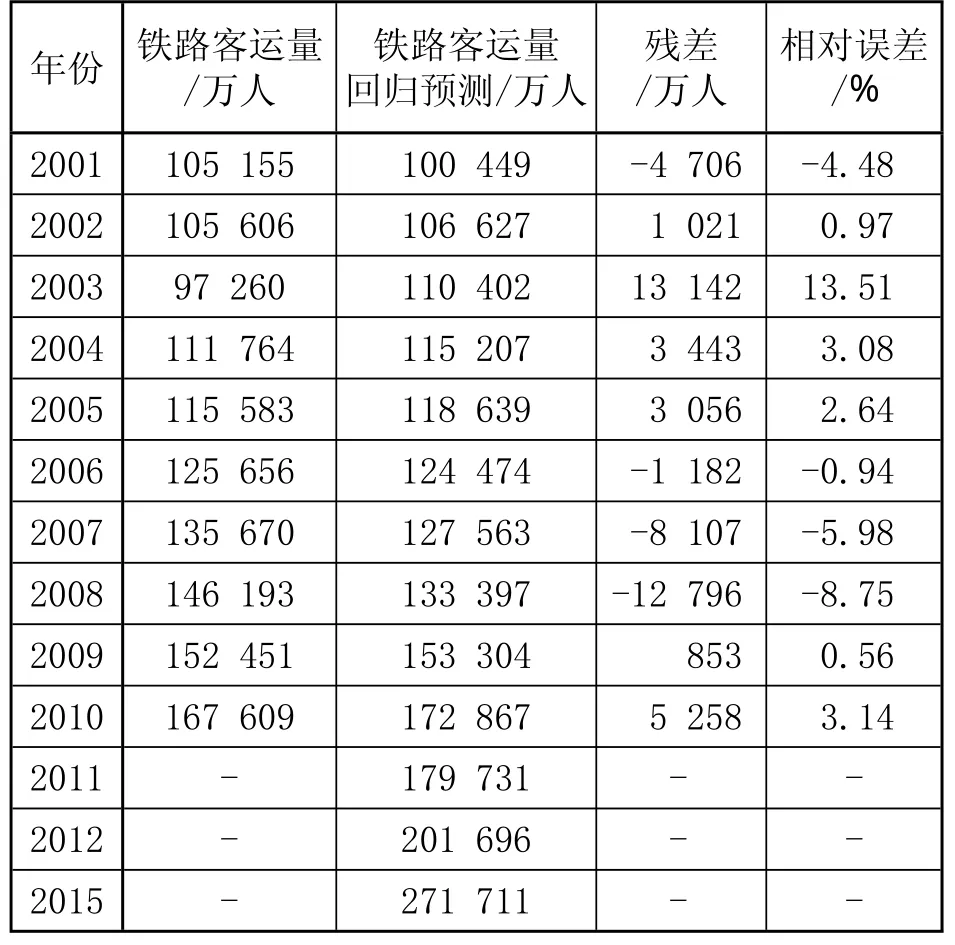
表2 鐵路客運量回歸預測相關數據

2.2 回歸-馬爾可夫預測模型確定預測值

馬爾可夫鏈是根據系統狀態之間的轉移矩陣來描述一個隨機動態系統未來的發展狀況，轉移概率(即在事件的發展變化過程中，從某一種狀態出發下一時刻轉移到其他狀態的可能性) 則反映了各狀態之間某種內在的規律性。其中，n 步狀態轉移矩陣的計算為：

P(n) 描述了 m個狀態相互轉移的概率分布。其中，pij為由狀態 i 轉移到狀態j 的概率[7-8]。如 p12表示由狀態1轉移到狀態2的概率。下一時刻向各狀態轉移的概率 P(E) 為：

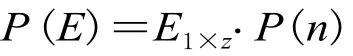
其中 E1×z是一個1行 z 列的矩陣，為當前時刻的狀態矩陣，z 為劃分的狀態區間。

回歸—馬爾可夫預測模型的基本思想是先用回歸預測模型進行預測。然后根據回歸預測數據與原始數據的相對誤差將各原始數據年劃分狀態。再根據各年所處狀態求得狀態轉移矩陣，進行未來相關數據的預測。

2.2.1 狀態劃分

根據表2中的相對誤差列，將原始數據按年劃分為4個狀態，劃分標準如表3所示。例如，2009年的回歸預測相對誤差為 0.56%，則該年屬于狀態 3。

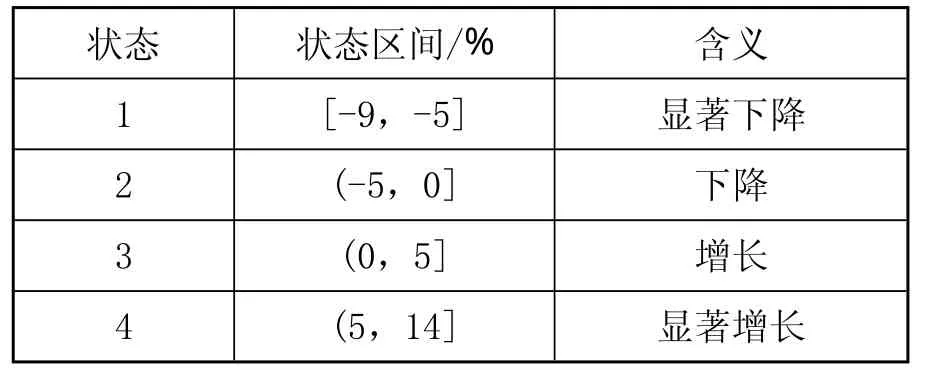
表3 狀態劃分區間及各狀態含義

2.2.2 狀態轉移

鐵路客運量在 2001—2010年中各類狀態的一步轉移情況如表4所示。例如，表4中第二行的數據含義為：由狀態 1一步轉移到狀態1和一步轉移到狀態3的情況各出現了1次，合計為2次。表4中的其他數據依次類推。

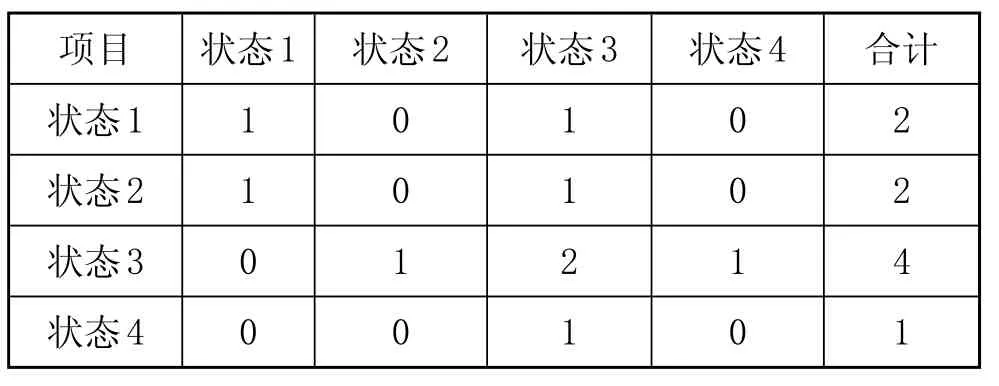
表4 回歸預測結果馬爾可夫狀態轉移

2.2.3 數據預測

根據 2001—2010年鐵路客運量數據，以2010年為當前時間點預測 2011年鐵路客運量，需要計算一步狀態轉移矩陣；預測 2012 與 2015年的鐵路客運量，需要分別計算二步狀態轉移矩陣與五步狀態轉移矩陣。下面以運用回歸—馬爾可夫模型預測2011年鐵路客運量為例，說明該模型的具體計算過程。

從狀態的轉移表可確定馬爾可夫一步狀態轉移矩陣P (1)。

由于 2010年鐵路客運量所處的狀態為狀態 3，對應 2010年的狀態矩陣為 (0，0，1，0)，因而 2011年鐵路客運量轉向各狀態的概率為：

即 2011年鐵路客運量有 0.25 的概率處于狀態2和狀態 4，有 0.5 的概率處于狀態 3。

由各狀態區間的預測中值，分別乘以預測年可能處于該狀態的概率再求和，即：175 238×0.25＋184 225×0.50＋196 806×0.25＝185 124(萬人)，得到 2011年鐵路客運量回歸—馬爾可夫預測值為185 124萬人。同理，計算得到 2012年和 2015年鐵路客運量的預測結果，如表5所示。

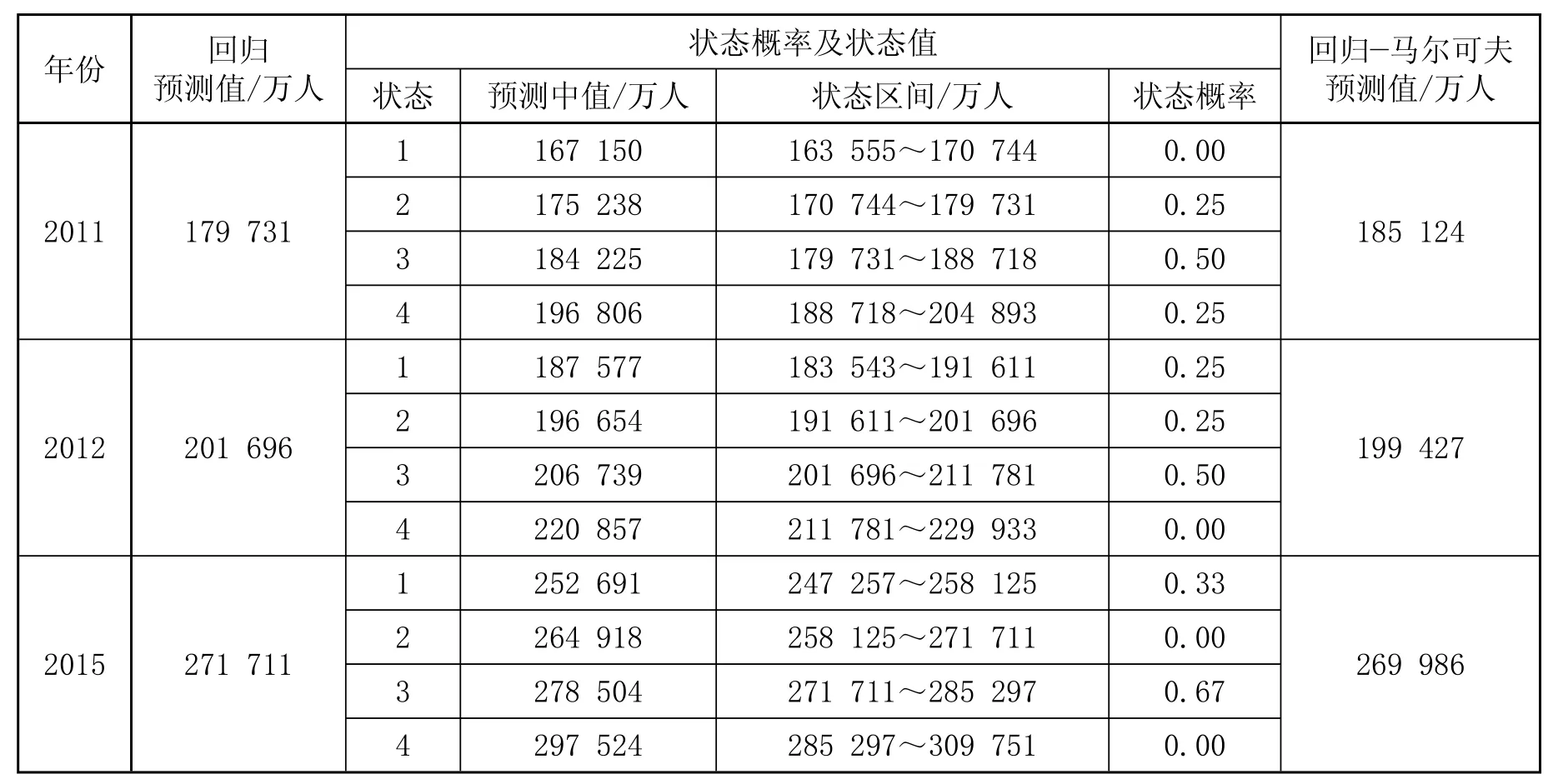
表5 鐵路客運量回歸-馬爾可夫預測值

3 結束語

基于回歸—馬爾可夫預測模型的 2011年、2012年鐵路客運量預測值分別為 185 124萬人和 199 427萬人，與 2011年實際數據和 2012年預計數據的誤差為-0.04% 和 -1.72%。因此，在鐵路客運量預測方面，對線性回歸預測模型結果進行馬爾可夫鏈改進的方法能夠提高預測的準確性。但還需通過更多的實際數據對預測模型的可靠性進行驗證，以不斷完善回歸—馬爾可夫預測模型。

[1]郭孜政. 鐵路客運量影響因素層次結構分析[J]. 交通運輸工程與信息學報，2007(4)：68-71.

[2]王傳峰. 既有線提速后的客運量預測研究[D]. 四川：西南財經大學，2008.

[3]侯麗敏，馬國峰. 基于灰色線性回歸組合模型鐵路客運量預測[J]. 計算機仿真，2011(7)：1-3，30.

[4]謝孝如，蔣惠園，申耀偉. 基于并聯灰色—線性回歸組合模型的客運量預測[J]. 鐵道運輸與經濟，2008(8)：92-94.

[5]田自力，劉碧發. 灰色馬爾可夫鏈預測模型[C]. 臺灣第一屆灰色系統理論與應用研討，1996：157-161.

[6]國家統計局. 中國統計年鑒：1999—2011 [M]. 北京：中國統計出版社，1999—2011.

[7]關 靜. 中國民航旅客吞吐量的灰色馬爾可夫模型預測[J].中國民航大學學報，2010(2)：45-47.

[8]張 誠，張廣勝. 基于優化灰色—馬爾可夫鏈模型的鐵路貨運量預測[J]. 物流技術，2011(13)：129-142.