災難救援應急物資配送問題的研究現狀及發展方向

陳 剛，彭永濤

(西南交通大學 交通運輸與物流學院，四川 成都 610031)

近年來各種災難頻發，無論是 2004年的印度洋海嘯、2008年的汶川地震，還是 2010年的海地地震及 2011年的日本地震海嘯都造成了大量的人員傷亡和財產損失。據統計，全球每年發生的災難達 500次以上，75 000 人因此而死亡，2億人受災[1]。災難的發生導致大量應急物資需求，而快速準確地將應急物資運送到受災點是災難救援的關鍵，因而應急物資的分配和應急車輛路徑的選擇成為災難救援研究的2個核心問題。有關文獻從不同角度或分類對應急物流進行了綜述[1-2]。從問題類型及解決方法的角度，結合災難救援應急物資配送問題分類綜述，探討相關問題研究具有重要的現實意義。

1 應急物資分配問題

1.1 基于數學組合方法

基于數學組合方法的應急物資分配問題實際上是出救點選擇問題，問題的基本數學描述如下[3]：A1，A2，…，An為 n個應急物資出救點，A 為受災點，x 為應急物資需求量，Ai的物資可用量為 xi(xi>0)≥x(i=1，2，…，n)，從Ai到 A 需要的時間為ti(ti>0)，設t1≤t2≤…≤tn，要求給出一方案(確定參與應急的出救點及各自提供的應急資源數量)，在滿足約束條件下使應急開始時間最早。

國內最早開始研究應急物資分配問題的是劉春林等[4-6]，考慮在應急物資連續供應條件下，分別以應急開始時間最早、出救點數目最少、使應急開始時間不遲于限制期 t 的可能度最大的方案等為優化目標，并通過組合優化、模糊規劃、兩階段規劃等方法求解模型。這些研究僅限于單受災點、單物資種類，適合電力供應系統、供暖供氣系統及消防救援系統等連續性應急系統，但不適合大規模突發事件的救援活動。此后，國內學者對這個問題進行了深入研究，增加了總費用最小[7]、損失最小或滿意度最大[8]等目標，應急物資種類由1種擴展到多種[9]，受災點也由1個擴展到多個[10]，出救點選擇問題研究進展情況如表1所示。

表1 出救點選擇問題研究進展情況

1.2 基于模糊聚類方法

Sheu和Chen[11]針對大規模災難應急物資分配問題，提出了一個3階段優化算法，第1階段基于應急物資需求及優先權對災區進行模糊聚類，第2階段根據聚類結果進行物資分配，第3階段根據物資分配結果規劃車輛路徑。在此基礎上，Sheu[12]考慮了時變需求預測和動態供給情形，以臺灣地震為研究背景，提出一個由應急物資商、應急物資配送中心及受災地構成的3層應急物流概念框架，并為關鍵救援時期響應應急救援需求的應急物流共同配送提出了一個混合模糊聚類優化方法。在其最新研究成果中，Sheu[13]提出一個不完整信息條件下大規模自然災害動態應急物資需求管理模型，該模型包含基于數據融合的需求預測、模糊聚類受災區域、對受災區域分組的優先權進行排序3個步驟。

1.3 基于網絡流理論

Haghani和Oh[14]基于時空網絡的概念，把災難救援問題處理為大規模、多商品、多運輸方式帶時間窗的網絡流問題，提出了2種啟發式算法，一種算法利用問題的內在網絡結構和約束條件將模型分解為子問題求解，另一種算法是利用交互式修復和運行方式，即在每次迭代逐步固定整數變量，直到所有整數變量都為定值。Tzeng等[15]考慮到公平性，提出了一個多目標規劃方法，3個目標分別為總成本最小、總運行時間最短及物資需求滿足率最大，前2個目標追求的是效益，第3個目標考慮的是公平，保證應急物資配送到所有的需求點。Yi和 Kumar[16]提出用蟻群優化算法解決應急救援活動中的物流問題，把原來的應急物流問題分解為構建車輛路徑和多種類物資調度2個階段，第1階段在蟻群算法信息素軌跡的引導下建立隨機車輛路徑，第2階段建立了基于求解程序 (Solver) 的網絡流來解決不同車輛流和物資之間的分配問題。Yan和 Shih[17]認為應急物資配送及中斷道路搶修之間是有關聯的，為應急物資配送及中斷道路搶修構建了時空網絡，并以總時間最短為目標建立了一個多目標、多商品的混合整數網絡流模型。

1.4 基于其他理論和方法

大規模突發事件往往會中斷路網，正常的車輛配送無法進行，Barbarosoglu等[18]為災難救援運作中直升機任務計劃建立了一個雙層數學規劃模型，上層為戰術層，決策直升機隊的組合、飛行員的分配及直升機的任務；下層為操作層，決策直升機的路徑、裝卸配送計劃及燃料補充計劃。Chang 等[19]基于情景規劃方法將洪水應急物流問題描述為2個隨機規劃模型，借助地理信息系統提出模型的解決方法，為政府部門洪水災害應急物流提供決策工具。楊繼君等[20]設計了應急資源調度的多模式分層網絡，提出了基于合作博弈的應急資源調度模型與求解算法，將應急資源的合理調度問題轉化為對合作博弈調度模型的核心求解問題。

2 應急車輛路徑問題

車輛路徑問題 (VRP) 一直是網絡優化問題中最基本的問題之一，國內外關于車輛路徑問題的研究已經很多。目前大部分 VRP 問題的研究都是在商業背景下，主要以成本最小為目標，應急背景下的 VRP 問題研究不多，主要以應急時間最短或災區損失最小為目標。Lin 和 Batta[21]結合軟時間窗、多周期及分批配送的車輛路徑問題，為災難救援運作關鍵物品配送問題提出了一個多目標整數規劃模型。陳森等[22]利用物資要素和時延要素之間的轉換，同時考慮搶修路段和車輛配送，建立了路網結構、車輛路徑聯合優化模型，提出基于遺傳算法和動態規劃的求解算法。田軍等[23]借助模糊數學中的三角模糊數描述應急物資需求量，利用聯系速度時間依賴函數模擬真實的動態路網交通狀況，建立應急物資配送動態調度多目標數學模型。徐志宇等[24]建立了分批配送車輛路徑模型 (SDVRP)，實現為滿足需求最小化、總配送時間最短化、各受災點失衡度最低化3大目標，但只是通過簡單的加權平均將多目標轉化成單目標，同時模型也只考慮了單出救點和單物資品種。應急車輛路徑問題目前研究的目標約束及算法如表2所示，在這些模型中受災點的物資需求量都是已知的。

應急車輛路徑問題拓展標準如表3所示。從目標函數來看，單目標研究較多，多目標研究較少；從供應特征來看，目前的研究大多數是單出救點，但多出救點、多品種、多周期是未來研究的發展趨勢；從需求特征來看，目前的研究大多是需求量確定的情況，也有少部分學者開始考慮模糊或時變需求，并在建模的時候考慮時間窗；從車輛特征來看，應急救援一般都考慮車輛數有限、車容量不同的情況；從運輸方式來看，目前還都是以單一的運輸方式為主；從解決方法來看，由于都是 NP-hard問題，沒有人用精確算法，大部分學者考慮用啟發式算法解決問題，仿真研究也相對較少。

3 研究方向

盡管應急物資配送問題的研究已經有了一定的成果，但與大規模突發事件應急救援的實踐需要還有一定的差距，未來應急物資配送問題的研究可以主要集中在以下方面。

（1）考慮應急物資需求不確定的情況。目前大多數文獻都是考慮需求已知的情況，但災難發生后，災區一般都比較混亂，統計工作難以開展，必須通過其他手段來明確各個受災點的物資需求量。

表2 應急車輛路徑問題目前研究的目標約束及算法

（2）建立更符合實際災難救援的應急物資配送模型。目前所查閱到的國內外文獻都只考慮了應急救援的某個階段，未能全面描述應急物資從儲備庫到配送中心再到受災點的配送場景，不能完全用來指導應急救援實踐。

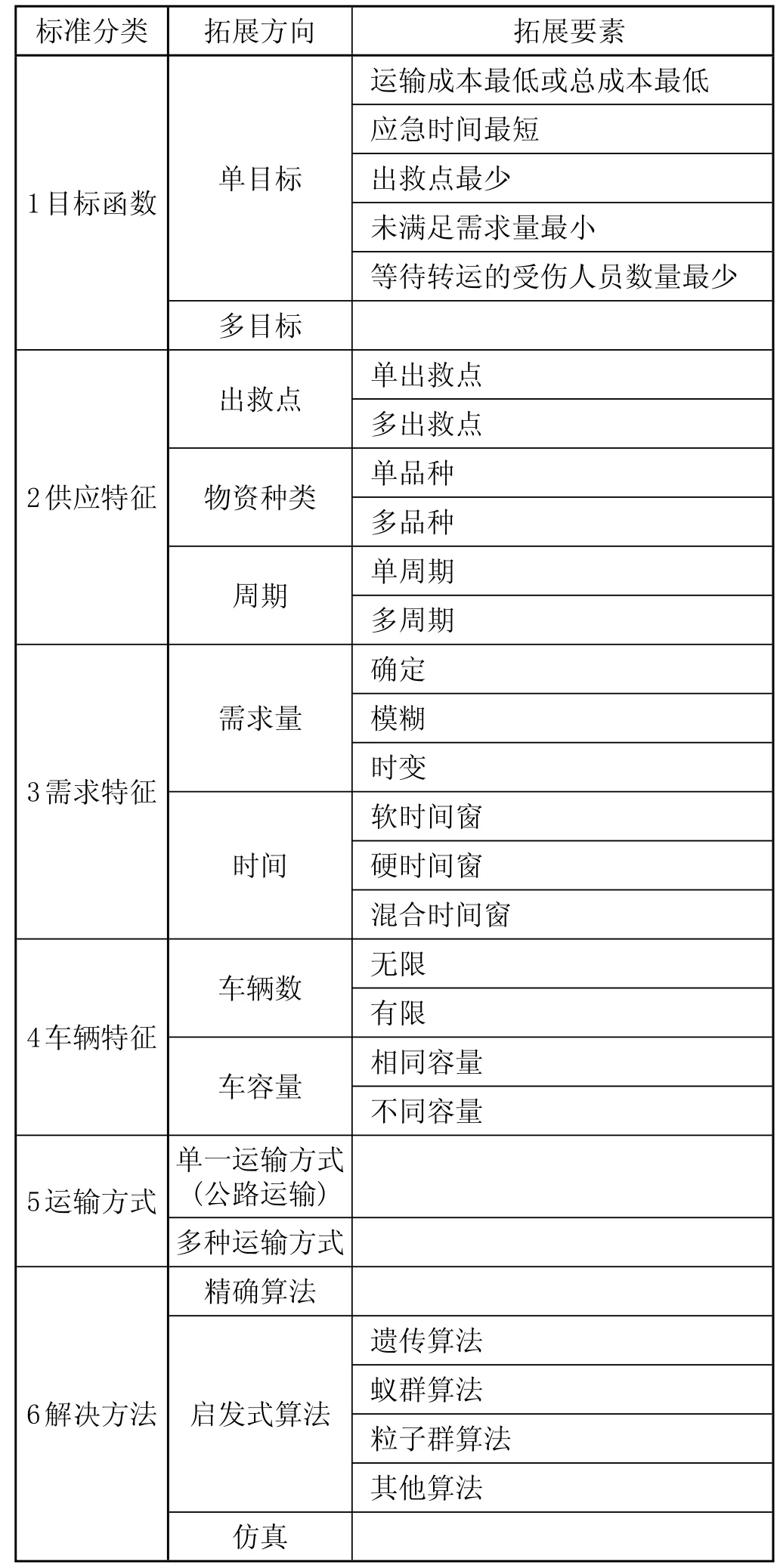
表3 應急車輛路徑問題拓展標準

（3）探索更快速更有效的算法。目前求解應急物流優化模型的算法主要有遺傳算法、蟻群算法、粒子群算法等，在解決多目標模型時遺傳算法具有較好的適應性，而蟻群算法和粒子群算法在解決單純的路徑問題時優勢明顯，因此可以進一步研究這幾種算法的融合，提出更加快速高效的啟發式算法。

（4）結合其他理論研究應急物資分配問題。應急物資分配方案的多利益/多目標沖突決策，與博弈論的最大化個人支出收益思想接近，控制論中的魯棒規劃作為不確定信息處理方法，可以很好地解決應急物資配送問題中的信息不確定性對于決策的影響，這些理論為應急物資配送研究提供了新思路。

[1]Caunhye A M，Nie X，Pokharel S. Optimization Models in Emergency Logistics A Literature Review[J]. Socio-Economic Planning Sciences，2012，46(1)：4-13.

[2]Altay N，Green W G. OR/MS Research in Disaster Operations Management[J]. European Journal of Operational Research，2006(175)：475-493.

[3]劉春林，盛昭瀚，何建敏. 基于連續消耗應急系統的多出救點選擇問題[J]. 管理工程學報，1999， 13(3)：13-16.

[4]劉春林，何建敏，施建軍. 一類應急物資調度的優化模型研究[J]. 中國管理科學，2001，9(3)：29-36.

[5]劉春林，施建軍，李春雨. 模糊應急系統組合優化方案選擇問題的研究[J]. 管理工程學報，2002， 16(2)：25-28.

[6]劉春林，沈厚才. 一類離散應急供應系統的兩目標優化模型[J]. 中國管理科學，2003，11(4)，27-31.

[7]俞武揚. 大規模應急物資中轉運輸問題研究[J]. 計算機工程與應用，2011，47(17)：1-3，30.

[8]潘 郁，余 佳，達慶利. 基于粒子群算法的連續性消耗應急資源調度[J]. 系統工程學報，2007，22(5)：556-560.

[9]葛洪磊，劉 南，張國川，等. 基于受災人員損失的多受災點、多商品應急物資分配模型[J]. 系統管理學報，2010，19(5)：541-545.

[10]王蘇生，王 巖，孫 健，等. 連續性條件下的多受災點應急資源配置算法[J]. 系統管理學報，2011， 20(2)：143-150.

[11]Jiuh-Biing Sheu Y C. A Novel Model for Quick Response to Disaster Relief Distribution[J].Proceedings of the Eastern Asia Society for Transportation Studies，2005(5)：2454-2462.

[12]Sheu J. An Emergency Logistics Distribution Approach for Quick Response to Urgent Relief Demand in Disasters[J].Transportation Research Part E，2007(43)：687-709.

[13]Sheu J. Dynamic Relief-demand Management for Emergency Logistics Operations under Large-scale Disasters[J].Transportation Research Part E，2010(46)：1-17.

[14]Haghani A，Oh S. Formulation and Solution of a Multicommodity Multi-modal Network Flow Model for Disaster Relief Operations[J]. Transportation Research Part A，1996，30(3)：231-250.

[15]Tzeng G，Cheng H，Huang T D. Multi-objective Optimal Planning for Designing Relief Dilivery Systems[J].Transportation Research Part E，2007(43)：673-686.

[16]Yi W，Kumar A. Ant Colony Optimization for Disaster Relief Operations[J]. Transportation Research Part E，2007(43)：660-672.

[17]Yan S，Shih Y. Optimal Scheduling of Emergency Roadway Repair and Subsequent Relief Distribution[J]. Computer&Operations Research，2009(36)：2049-2065.

[18]Barbarosoglu G，Ozdamar L，Cevik A. An Interactive Approach for Hierarchical Analysis of Helicopter Logistics in Disaster Relief[J]. European Journal of Operational Research，2002(140)：118-133.

[19]Chang M，Tseng Y，Chen J. A Scenario Planning Approach for the Flood Emergency Logistics Preparation Problem under Uncertainty[J]. Transportation Research Part E，2007(43)：737-754.

[20]楊繼君，吳啟迪，程 艷，等. 面向非常規突發事件的應急資源合作博弈調度[J]. 系統工程，2008， 26(9)：21-25.

[21]Lin Y，Batta R. A Logistics Model for Emergency Supply of Critical Items in the Aftermath of a Disaster[J]. Socio-Economic Planning Sciences，2011，45(4)：132-145.

[22]陳 森，姜 江，陳英武，等. 未定路網結構情況下應急物資車輛配送問題模型與應用[J]. 系統工程理論與實踐，2011，31(5)：907-913.

[23]田 軍，馬文正，汪應洛，等. 應急物資配送動態調度的粒子群算法[J]. 系統工程理論與實踐，2011，31(5)：898-906.

[24]徐志宇，彭嘉臻，許維勝. 應急物流的分批配送規劃及蟻群優化求解[J]. 計算機工程與應用，2011，47(24)：1-3.