激光散斑的亞像素位移法計算及比較

王希軍

(中國科學院長春光學精密機械與物理研究所，吉林長春130033)

1 引言

數字散斑相關方法(Digital Speckle Correlation Method，DSCM)是一種有效的光學測量手段。與傳統的干涉測量方法不同，它直接從物體表面隨機分布的人工或自然散斑場中提取位移和變形信息，不需要復雜的干涉條紋處理過程，具有全場測量、非接觸等優點，且其光路簡單，對測量環境要求不高，因而被廣泛應用于實驗力學及其他科學研究領域［1-4］。

在數字散斑相關測量中，獲取的數字散斑圖是離散的灰度信息，經相關運算后，得到整像素為單位的位移值，而物體的真實位移值不一定恰好是整像素，因此，亞像素相關測量方法已成為數字散斑相關測量中的關鍵技術和研究重點。

目前，國內外常用的亞像素相關測量方法有插值法［5-6］、曲面擬合法［7］、牛頓-拉夫森法［8］、梯度算法［9-10］、頻域相關算法［10-11］以及遺傳算法［12］等。雖然對這些計算算法的精度分析研究開展得較早，但很少有利用算法分析和計算激光散斑圖并比較各種算法精度的工作，因此，根據不同的測量要求選擇合適的亞像素算法對于提高激光散斑相關測量技術的精度和計算速度等工作顯得尤為重要。

本文逐一比較了插值算法、梯度算法和牛頓-拉夫森迭代算法的精度和效率。分析了處理激光散斑圖時這些算法的特點及適用性，為滿足激光散斑相關測量數據處理和計算精度的特定要求，提供選擇亞像素計算方法的依據。

2 亞像素計算散斑位移圖

散斑場中各點周圍的鄰近區域通常稱為子集或窗口。選取散斑場中某一點為中心的窗口作為該點位移和形變的信息，分析和搜索該窗口的移動和變化，可獲得該點的位移和形變信息。在進行數字散斑相關測量過程中，首先在物體變形前后拍攝兩幅散斑圖，如圖1所示。在變形前的散斑圖(參考圖)中以待測點P為中心取m×m的子區A，當被測物體發生形變后，即在物體變形后所拍的散斑圖中(目標圖)，子區A移至子區B的位置，相應P點移動到P'。由統計學可知，A與B兩個樣本空間的相關系數最大。因此可以根據相關系數的最大值來確定子區B的位置，從而得到P 點的位移［(x'－x)，(y'－y)］。

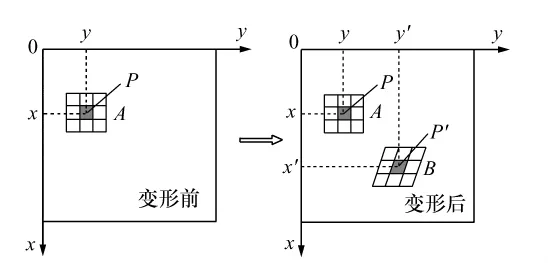
圖1 數字散斑相關方法測量原理示意圖Fig.1 Schematic diagram of digital speckle correlation method

但通過上述方法只能得到整像素位移，而物體實際的位移值往往不是整像素，并且整像素的位移定位精度是遠遠不夠的，需要進行亞像素相關測量。常用的亞像素相關方法有插值法、牛頓-拉夫森法及梯度法。

2.1 相關系數插值法

該方法先用十字搜索法或其它整像素搜索方法算出子區的整像素位移，然后對整像素位移點相鄰9×9點的相關系數矩陣進行二維插值。插值函數可以為雙線性插值、雙三次樣條插值函數等，一般雙三次樣條插值和雙線性插值具有較高的精度［13］。相關系數插值法的算法比較容易實現，但計算量較大。本文主要討論采用雙三次樣條插值計算激光散斑圖的結果。

2.2 梯度算法

基于梯度的亞像素位移算法最初由Davis和Freeman［9］提出，該方法假設物體只發生剛體運動。當物體發生微小變形且選擇的計算子區足夠小時，則該子區即可近似剛體運動。令f(x，y)，g(x*，y*)分別表示物體變形前后子區的灰度，則:

式中:u，v分別為子區在x，y方向上的整像素位移，Δx，Δy分別為子區在x，y方向上的亞像素位移。選取最小平方距離相關函數作為子區匹配的算子，則:

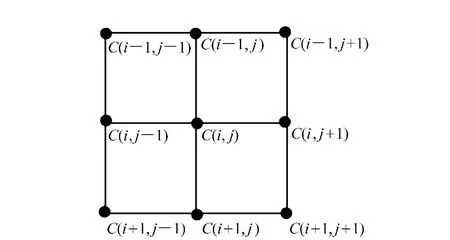
圖2 鄰域相關系數矩陣差值示意圖Fig.2 Schematic diagram of neighborhood correlation coefficient matrix interpolation

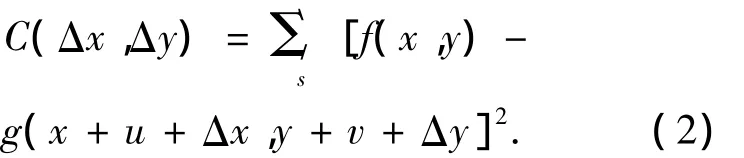
真實的亞像素位移Δx，Δy應使式(2)取得最小值，因此由極值條件:

式中，gx，gy為灰度的一階導數。

2.3 牛頓-拉夫森迭代算法

牛頓-拉夫森迭代法最初由 Bruck［8］提出，由于在算法中引入了位移的一次導數，因此其可以對具有形變的圖像子區進行計算。

令f(x，y)為樣品變形前拍攝的散斑圖的灰度分布，g(x'，y')為變形后對拍攝的散斑圖的灰度分布。對于變形前散斑圖的某一子區灰度分布fs(x，y)，設其在變形后對應于灰度分布 gs(x'，y')，則應有 gs(x'，y')=fs(x，y)，且應有以下對應關系:

式中:u為變形后子區中心(x0，y0)在x方向上的位移，v為變形后子區中心(x0，y0)在y方向上的位移，Δx，Δy為點(x，y)到子區中心(x0，y0)的距離，?u/?x，?u/?y，?v/?x，?v/?y 為位移的一階偏導數。選取最小平方距離相關函數:

由式(6)可見，子區 f(x，y)與 g(x'，y')的相關系數C是關于子區位移和形變參數的函數，令P=(u，v，ux，uy，vx，vy)T，即 C=C(P)。顯而易見，當P取得子區真實的位移和形變參量時，相關系數應為最小值。因此可以通過式(6)的極值條件:

求出子區的位移和形變參數。式(7)可以用迭代法求解。令P0為迭代初值，P'為式(7)的解，對相關系數C(P')在P0點做泰勒級數展開，得:

牛頓-拉夫森迭代法需要用其他算法獲得整像素位移值作為迭代初值，否則將嚴重影響收斂速度。

3 計算結果及討論

采用數值模擬的仿真散斑圖對上述3種算法的精度進行了比較。激光散斑圖來自于磁流體干燥過程實驗，如圖 3所示［14］。

圖3 磁流體干燥實驗中的激光散斑圖Fig.3 Typical laser speckle diagram of the magnet fluid drying

在相關搜索算法中需要首先選擇模板窗口，選取大模板窗口可以降低噪聲的影響，提高計算精度，但大的窗口意味著要計算更多的點，因此計算效率會降低。

Zhang在文獻［15］中分析了窗口大小對計算精度和計算效率的影響，他指出窗口選取在31 pixel×31 pixel到51 pixel×51 pixel之間可以在精度和效率之間獲得較好的平衡。本文選取窗口為 41 pixel×41 pixel。

類似文獻［9］方法，截圖以512×512為參考，不失一般性地模擬出平移0.01～0.09 pixel(行方向上)，間隔0.01 pixel的 9幅散斑圖和平移0.1～0.9 pixel(列方向)，間隔為0.1 pixel的9幅位移散斑圖，共模擬出1幅基準散斑圖和18幅位移散斑圖。

然后，分別用3種算法計算18幅相對于基準散斑圖的位移散斑圖，得到了3種亞像素算法偏差均值圖如圖4所示和標準差圖如圖5所示。

從圖4中可以看出，在這3種算法中梯度算法的偏差均值在整個預設位移范圍0.01～0.9 pixels內絕對值都是最小的，在±0.001 pixels之內;牛頓-拉夫森迭代算法在位移為0.01～0.1 pixels時較插值算法的均值誤差小，在位移為0.1～0.9 pixels時，牛頓-拉夫森迭代算法和插值算法的平均誤差相當，達到±0.003 pixels。但就處理激光散斑圖的算法而言，梯度算法處理精度最好，插值法的處理精度最差，牛頓-拉夫森迭代算法的處理精度居中。標準差表示數據的誤差分布，標準值越小，誤差分布越小，故可用它來評價算法的穩定性。從圖5標準差曲線可以看出，梯度算法在3種算法中標準差值最小，但在0.5 pixel位移圖計算時是個例處，插值算法的標準差最大。因此，在3種算法中，梯度算法最穩定，而插值算法最不穩定。至于梯度算法在位移0.5 pixels處產生了較大的標準差，潘兵在文獻［16］給出的解釋:式(3)在做泰勒展開時的截斷誤差為o(h)2，這是位移為0.5 pixel時達到最大值所致。

圖4 3種算法的均值誤差Fig.4 Means bias error of three methods

圖5 3種算法的標準差Fig.5 Standard deviation of three methods

表1 3種算法的計算時間(以插值算法的用時為歸一單位)Tab.1 Computing consuption of three methods

表1給出了3種算法的相對時間比較，3種算法是用Matlab編程實現的，計算機的CPU為Intel Pentium D，主頻2.8 GHz，內存2 G。通過比較中可以看出，梯度算法和插值算法的用時相當，略高于插值算法;而牛頓-拉夫森迭代算法用時最長，約是插值算法的9倍。這是由于牛頓-拉夫森算法中每次迭代都要對相關系數矩陣進行插值運算，而在插值算法和基于梯度的算法中只進行了一次插值運算。綜合比較3種算法的精度、穩定性和用時，可以看出，在處理激光散斑圖時，梯度算法優于其它兩種算法。

4 結論

本文介紹了數字散斑圖像相關法的位移測量原理以及較常用的插值算法、梯度算法和牛頓-拉夫森迭代算法3種亞像素位移算法及特點。同時利用算法得到了激光散斑圖計算的偏差均值曲線和標準差曲線。利用偏差均值的物理意義，比較出梯度算法在亞像素計算散斑圖時的精度較高。通過標準差曲線得出梯度算法在亞像素計算散斑圖時的穩定性較好。盡管梯度算法用時略高于插值法，但對于激光散斑測量小位移實驗或連續剛性位移實驗，梯度算法比較有效，應作為優先考慮的算法。

當像素位移量高達0.5時，梯度算法產生了較大誤差。此時牛頓-拉夫森迭代法和插值法在0.5～0.9 pixels區間的偏差均值較小，對于激光散斑測量大位移或振動實驗，它們的標準差在0.003 pixels之內。

［1］ PETERS W H，RANSON W F.Digital imaging techniques in experimental stress analysis［J］.Opt Eng.，1981，21:427-431.

［2］ 邢冬梅，李鴻琦，李林安，等.梯度功能材料穩態溫度場下的熱應力分析［J］.功能材料，2002，33(5):505-507.XING D M，LI H Q，LI L A，et al..Study on thermal strain field of functional gradient material in steady temperature［J］.Functional Material，2002，33(5):505-507.(in Chinese)

［3］ 云禮寧，馬少鵬，李霞鎮，等.用數字散斑相關方法研究竹材在拉伸載荷下的斷裂行為［J］.北京理工大學學報，2011，31(3):258-261.YUN L N，MA SH P，LI X ZH，et al..Experimental study of the fraxturc behavior of bamboo under tension based on digital speckle correlation method［J］.Transactions of Beijing Institute of Technology，2011，31(3):258-261.(in Chinese)

［4］ CHU T C，RANSON W F，SUTTON M A，et al..Applications of digital image-correlation techniques to experimental mechanics［J］.Exp.Mech.，1985，25:232-244.

［5］ PEARSON J J，HINES D C，GOLOSMAN S.Video-rate image correlation processor［J］.SPIE，1977，119:197-205.

［6］ DVORCHENKO V N.Bounds on(deterministic)correlation functions with applications to registration［J］.IEEE Trans Pattern Anal Mach Intell，1983，5(2):206-213.

［7］ 潘兵，續伯欽.數字圖像相關中亞像素位移測量的曲面擬合法［J］.計量學報，2005，26(2):128-134.PAN B，XU B Q.Subpixel registration using qradratic surface fitting in digital image correlation［J］.Acta Metrologica Sinica，2005，26(2):128-134.(in Chinese)

［8］ BRUCK H A，MCNEILL S R，SUTTON M A，et al..Digital image correlation using Newton Raphson method of partial di6erential correction［J］.Exp Mech，1989，29:261-267.

［9］ AVIS C Q，FREEMAN D M.Statistics of subpixel registration algorithms based on spatiotemporal gradients or block matching［J］.Opt Eng.，1998，37(4):1290-1298.

［10］ ZHOU P，GOODSON K E.Subpixel displacement and deformation gradient measurement using digital image/speckle correlation(DISC)［J］.Opt.Eng.，2001，40(8):1613-1620.

［11］ CHEN D J，CHIANG F P，TAN Y S，et al..Digital speckle-displacement measurement using a complex spectrum method［J］.Appl.Opt.，1993，32:1839-1849.

［12］ ORIAT L，LANTZ E.Subpixel detection of the center of an object using a spectral phase algorithm on the image［J］.Pattern Recognition，1998，31:761-771.

［13］ 李慶揚，王能超.易大義編著，數值分析［M］.北京:清華大學出版社，2008.LI Q Y，WANG N CH，YI D Y.Numerical Analysis［M］.Beijing:Tsinghua University Press，2008.(in Chinese)

［14］ 李新忠，岱欽，王希軍，等.用動態散斑法研究磁流體薄膜的干燥過程［J］.光電子·激光，2007，18(2):959-962.LI X ZH，DAI Q，WANG X J，et al..Dynamic speckle method for studying the drying process of magnet fluid film［J］.J.Optoelectronics·Laser，2007，18(2):959-962.(in Chinese)

［15］ ZHANG J，JIN G CH，MA SH P，et al..Application of an improved subpixel registration algorithm on digital speckle correlation measurement［J］.Optics Laser Technology，2003，35:533-542.

［16］ 潘兵，謝惠民，戴福隆.數字圖像相關中亞像素位移測量算法的研究［J］.力學學報，2007，39(2):245-252.PAN B，XIE H M，DAI F L.An investigation of sub-pixel displacements registration algorithms in digital image correlation［J］.Chinese J.Theoretical and Appl.Mechanics，2007，39(2):245-252.(in Chinese)