估計對流層延遲的單頻RTK卡爾曼濾波算法

徐彥田，程鵬飛，蔡艷輝，甄 杰，徐宗秋

(1.遼寧工程技術大學測繪學院，遼寧阜新123000;2.中國測繪科學研究院，北京100830)

估計對流層延遲的單頻RTK卡爾曼濾波算法

徐彥田1，程鵬飛2，蔡艷輝2，甄 杰2，徐宗秋1

(1.遼寧工程技術大學測繪學院，遼寧阜新123000;2.中國測繪科學研究院，北京100830)

提出一種對流層估計方法實現單頻RTK快速動態定位。用模型改正對流層干延遲，雙差對流層濕延遲用測站對流層天頂延遲估計，并與流動站位置及站間單差模糊度組成雙差方程進行卡爾曼濾波，得到單差模糊度浮點解及方差陣，通過星間求差得到雙差模糊度浮點解及方差陣，結合MLAMBDA方法實時確定模糊度。試驗驗證單歷元平面定位精度優于±3 cm，高程定位精度優于±10 cm。

單頻RTK;MLAMBDA;對流層天頂延遲(TZD);整周模糊度

一、引 言

GPS單頻接收機只能捕獲C碼和L1載波相位觀測值、多普測觀測值及導航電文，其成本較低、結構簡單，易與其他設備集成，因此，如何消除各種誤差的影響，利用相對廉價的便于攜帶的單頻接收機實現較大范圍、高精度實時定位是目前衛星大地測量研究的熱點和難點問題之一［1-2］。本文分析了對流層延遲的特點，將其分為干分量和濕分量，干分量的模型精度達到亞毫米級，而濕分量(約占10%)具有較強的時間性和空間性，其值達到10～40 cm，模型精度不能滿足高精度定位，差分技術不能有效削弱其影響。因此，本文將雙差對流層濕延遲用測站對流層天頂延遲進行一階馬爾可夫估計，并與流動站位置及站間單差模糊度組成雙差方程進行卡爾曼濾波，得到單差模糊度浮點解及方差陣，通過星間求差得到雙差模糊度浮點解及方差陣，結合MLAMBDA方法［3-7］逐歷元搜索模糊度。試驗驗證單歷元平面定位精度優于±3 cm，高程定位精度優于±10 cm。采用單差狀態向量的馬爾可夫過程避免了基星使用多次造成的相關性，但仍然保持了雙差的特性，并且單差模糊觀測值的權與高度角的關系更容易確定［8］。

二、雙差對流層延遲估計

對流層延遲分為干分量和濕分量，干分量的模型精度達到亞毫米級，而濕分量(約占10%)具有較強的時間性和空間性，其值達到10～40 cm，模型精度不能滿足高精度定位。為了估計濕分量的大小，采用一階高斯馬爾可夫過程估計測站對流層天頂濕分量，從而獲取信號傳播路徑上雙差對流層濕延遲，表示為

式中，Δ 為站星間雙差;ε為高度角;i為非基準衛星;j為基準衛星;A、B為測站標示;Mf()采用適用于大于3°衛星的NMF投映函數，即

三、單頻RTK卡爾曼濾波算法

1.單頻RTK卡爾曼濾波模型

將測站A、B的對流層天頂延遲組成觀測方程進行卡爾曼濾波估計，忽略軌道誤差和多路徑影響，采用站間單差模糊度，站星間雙差觀測方程的卡爾曼濾波方程可表示為

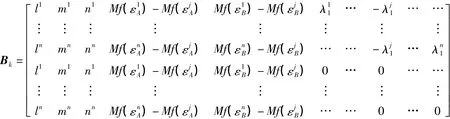
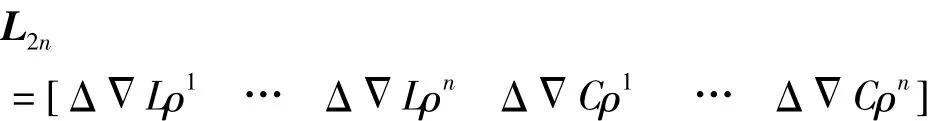
其中，Δ為站間單差;N為模糊度;ρ為站星間幾何距離;λ為波長

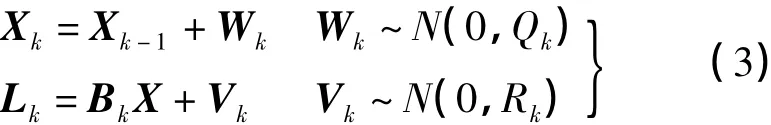
2.第k歷元濾波過程

第k歷元單點定位［X Y Z］k預報狀態向量的位置分量

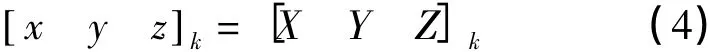
基于k－1歷元濾波誤差方差陣Pk－1和單點定位方差陣P［XYZ］k以及處理噪聲陣Qk計算k歷元預測誤差方差陣Pk，k－1

計算濾波增益陣Kk和改正數vk，修正第k歷元預測值得到卡爾曼濾波解為

最終解算得到站間單差模糊度浮點解及其方差陣，利用星間求差得到站間星間雙差模糊度浮點解及方差陣，結合MLAMBDA方法逐歷元固定模糊度。

四、試驗與分析

試驗采用IGS網站提供的GUAM和GUUG站數據，基線長18.678 km，數據為2009年3月4日(GPS時)的1000個歷元的觀測數據(采樣間隔為30 s，衛星截止高度角10°，總共解算模糊度17個，最多公共衛星數10顆。

由于站間基線距離較長，對流層延遲雙差后不能完全消除，根據以上的算法得到天頂對流層延遲，圖1顯示單站延遲絕對值最大值超過10 cm，前后歷元變化較小;兩站延遲最大差值為8 cm，因此將天頂對流層延遲分解成兩個狀態參數濾波是有必要的。

圖1 TZD濾波值示意圖

圖2為觀測時段較長的PRN15和PRN14衛星傳播方向上雙差對流層延遲。可以看出高度角較小時殘差較大，PRN14最大值達7.6 cm，近L1波長的一半，給模糊度固定帶來困難，而隨著衛星高度角的增大，雙差對流層延遲變小，衛星達到一定高度時可以忽略。

圖2 雙差大氣延遲殘差

圖3顯示濾波穩定后，雙差模糊度浮點解和固定解差值一般在1周以內，模糊度易于固定，搜索效率較高，并且Ratio值(見圖4)較大。由圖3和圖4可以看出，當可用衛星數頻繁變化時，模糊度濾波值相應出現較大抖動，Ratio值瞬時變小頻繁抖動，甚至出現固定失敗;而增加新升衛星時，由于模糊度初值和方差陣誤差較大，Ratio值急劇變小;對于穩定衛星數，Ratio值是遞增的。

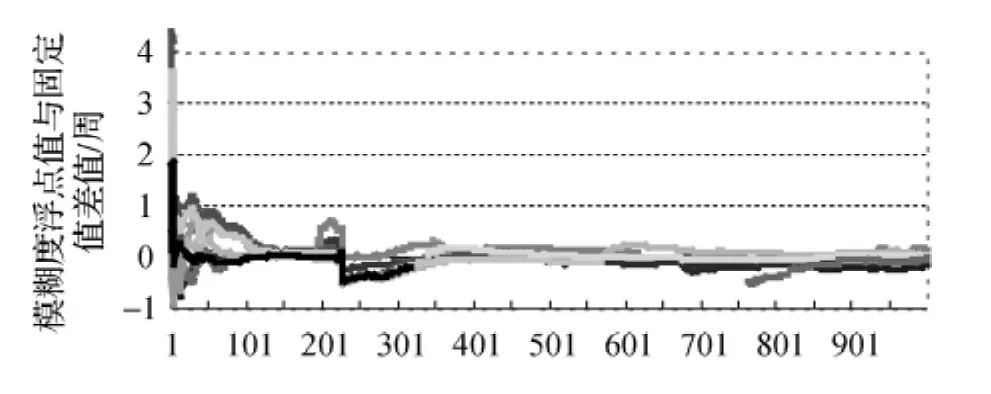
圖3 17個模糊度濾波值偏差示意圖

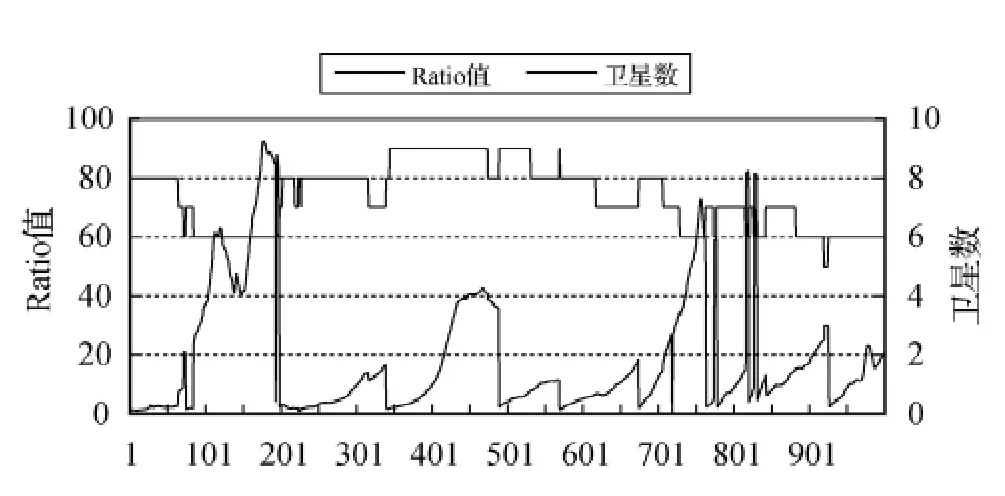
圖4 Ratio值與可用衛星數

通過MLAMBDA方法固定載波相位雙差模糊度后，改正流動站位置濾波值得到L1載波相位單歷元定位值，圖5顯示衛星數平穩時固定解平面定位精度優于 ±3 cm以內，高程定位精度優于±10 cm，濾波穩定后浮點解定位平面精度保持在±6 cm，高程精度保持在±15 cm內。

圖5 L1觀測值單歷元定位精度

五、結束語

經試驗驗證雙差對流層延遲殘差隨著高度角增加逐漸減小，高度角大于一定閾值時可以忽略其影響，測站天頂對流層延遲最大差值超過8 cm。若將天頂對流層延遲作為一個狀態參數進行濾波，投影到衛星路徑會影響模糊度浮點解精度，可能導致模糊度固定失敗，因此天頂對流層延遲分解成兩個狀態參數濾波是有必要的。濾波穩定后，雙差模糊度浮點解和固定解差值一般在1周以內，模糊度易于固定，搜索效率高;18 km基線固定解平面定位精度優于±3 cm，高程精度優于±10 cm，實現了單頻RTK快速動態定位，可滿足實際需要。

［1］ CHENG Pengfei.Investigation on the Establishment of DGPS Services in China［D］.Austria:the Graz University of Technology，1998.

［2］ 程鵬飛，蔡艷輝，文漢江，等.全球衛星導航系統［M］.北京:測繪出版社，2009.

［3］ 劉志平，何秀鳳，郭廣禮.GNSS模糊度降相關算法及其評價指標研究［J］.武漢大學學報:信息科學版，2011，36(3):257-261.

［4］ TEUNISSEN P J G.The Least-Squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Ambiguity Estimation［J］.Journal of Geodesy，1995，70:65-82.

［5］ CHANG W，YANG X，ZHOU T.MLAMBDA:A Modified LAMBDA Method for Integer Least-squares Estimation［J］.Journal of Geodesy，2005，79:552-565.

［6］ 周揚眉，劉經南，劉基余.回代解算的LAMBDA方法及其搜索空間［J］.測繪學報，2005，34(4):300-304.

［7］ TEUNISSEN P J G.A New Method for Fast Carrier Phase Ambiguity Estimation［C］∥Proceedings IEEE Position Locationand Navigation Symposium PLAN94. Las Vegas:［s.n.］，1994:562-573.

［8］ BENJAMIN W，REMONDI，GROVER B.Triple Differencing with Kalman Filtering:Making It Work［J］.GPS Solutions，2010(3):58-64.

A Kalman Filter Algorithm for Single-frequency RTK Solution

XU Yantian，CHENG Pengfei，CAI Yanhui，ZHEN Jie，XU Zongqin

0494-0911(2012)08-0004-03

P284

B

2011-11-03;

2012-03-02

中國測繪科學研究院基本科研業務費(7771017;7771202);地理空間信息工程國家測繪地理信息局重點實驗室開放基金(201103)

徐彥田(1983—)，男，河北石家莊人，博士生，研究方向為GNSS數據處理。