松江河梯級水電站短期優化調度數學模型分析

馮雁敏，張雪源，梁年生

(1.東北電力科學研究院有限公司，沈陽 110006;2.東北電網有限公司，沈陽 110180;3.華中科技大學，武漢 430074)

1 研究背景

松江河發電廠有4座水庫、3個電站、6臺水輪發電機組，各水庫調節性能不同，各電站區間來水復雜，電站間水頭、流量聯系緊密，各電站間水輪發電機組的型號及其動力特性不同，對運行方式的制約因素很多，難以根據調度管理人員的經驗找到最優運行方案。各電站間既存在著電力方面的聯系，又存在著水利、水力方面的聯系，上級電站發電用水和棄水經過一定時間流達下游水庫，將會影響下級各電站的發電，而下級電站的水庫調節能力又反過來影響上級電站的用水計劃［1－3］。梯級電站短期優化調度是一個強約束、非線性、多變量、多階段的大規模優化問題，其求解過程非常復雜。本文建立梯級電站發電量最大和發電效益最大2種數學模型，并將2種優化結果進行分析比較。

粒子群算法(Particle Swarm Optimization，PSO)是Kennedy博士和Eberhart教授于1995年提出的一種基于群體智能的仿生類隨機全局優化方法，該算法具有流程簡單、計算參數少、收斂速度快、魯棒性強等優點，適合求解梯級電站短期優化調度問題，但PSO存在2個主要缺陷:一是后期收斂速度慢，在較大的慣性系數作用下，粒子運動將遠離最優解;二是種群多樣性喪失較快，易陷入局部最優解而發生“早熟”現象。本文通過引入收縮因子和基于遺傳思想的變異算子對其進行改進，并應用其求解梯級電站短期優化調度問題［4－7］。

2 松江河梯級水電站概況

松江河梯級水電站位于頭道松花江上游支流松江河和漫江上，由松山引水工程和小山、雙溝、石龍3座水電站組成，其工程特性參數如表1所示。梯級電站以發電為主，總裝機容量為510 MW。由于石龍水庫調節性能較差，使梯級電站機組過流能力不匹配，導致石龍電站運行方式受到限制，應與雙溝電站聯合調度，合理安排開停機順序。

表1 松江河梯級水電站工程特性Table 1 The main parameters of Songjianghe cascade hydropower stations

3 梯級電站短期優化調度數學模型的建立

3.1 梯級電站短期優化調度數學模型

水電站的運行方式主要取決于其天然來水情況，在其運行方式變動對電網運行影響很小時，水電站可按自身最有利的方式運行，如在滿足日用水量要求和各種限制條件下使日發電量(或日發電收益)最大。松江河梯級電站自上而下為松山水庫、小山電站、雙溝電站、石龍電站，將水庫編號為i=1，2，3，…，I。I為水庫總數。將一個計劃日分成T個時段，t為時段順序編號，ΔT為時段間隔。日發電量最大和日發電效益最大目標函數如式(1)、(2)示:

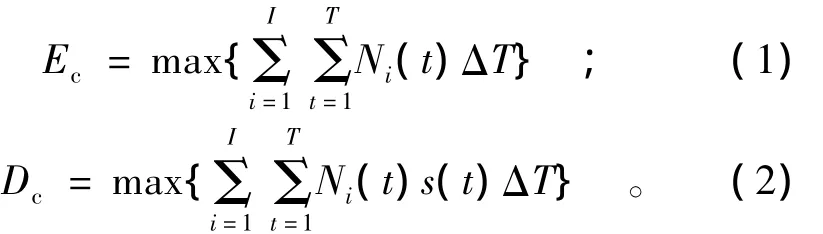
第i電站在t時段的出力計算式為

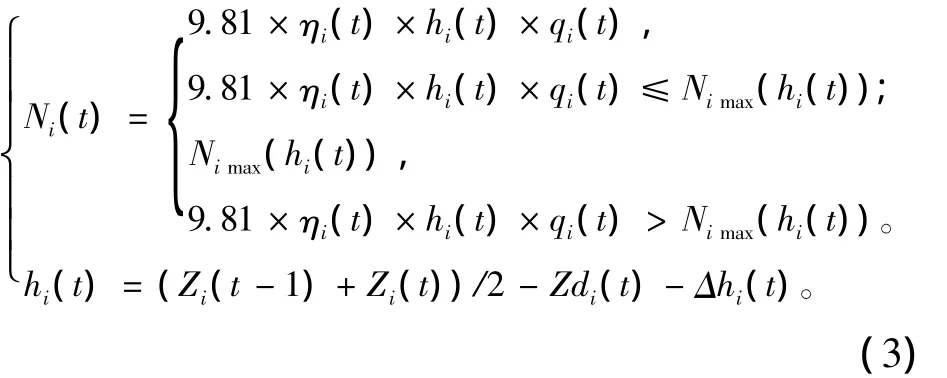
式中:Ec為梯級電站日最大發電量;Ni(t)為第i電站在第t時段出力;Dc為梯級電站日最大收益;s(t)為第t時段電價;ηi為第i電站在t時段的水輪發電機組效率;hi(t)為第i電站在t時段的工作水頭;qi(t)為第i電站在t時段的發電流量;Nimax(hi(t))為第i電站在對應水頭的最大限制出力;Zi(t－1)，Zi(t)分別為第i電站在第t時段初、末庫水位;Zdi(t)為第i電站在t時段的下游水位;Δhi(t)為第i電站在t時段的水頭損失。

3.2 約束條件

梯級電站短期優化調度主要約束條件如下。

(1)水量約束:

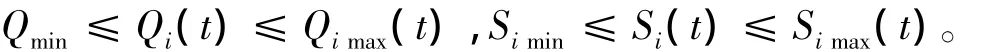
(2)水量平衡方程:

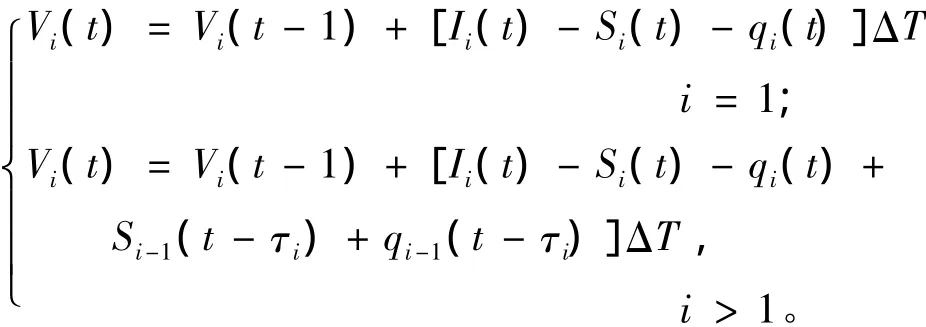
(3)水位約束:

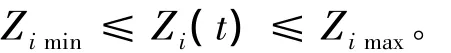
(4)出力約束:

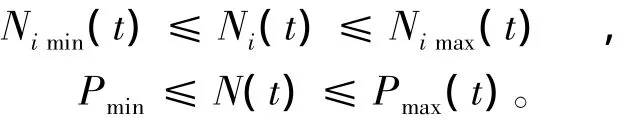
(5)其它約束:如機組完好狀態約束、避開水電機組強振區等。

式中:Qi(t)為第i電站第t時段的引用水量(包括發電流量和棄水流量);Ii(t)為水庫i在時段t內的自然入庫流量;Si(t)為水庫i在時段t內的棄水流量;τi為第i－1水庫水流流至第i水庫所需時間，即水流時滯;Zi(t)為第i電站在第t時段末的庫水位;Zimin(t)，Zimax(t)為第i電站在第t時段的最小、最大庫水位限制;Nimin(t)，Nimax(t)為第i電站在第t時段的最小、最大出力限制;N(t)為第t時段梯級電站的總出力;Pmin(t)，Pmax(t)為第t時段電力系統對梯級電站總出力最小、最大需求限制;Qimin(t)，Qimax(t)為第i電站在第t時段最小、最大引用流量限制;Simin(t)，Simax(t)為第i電站在第t時段最小、最大棄水流量限制。

4 粒子群算法及其改進

4.1 粒子群算法的基本原理

應用PSO求解優化問題時，問題的每個解對應于一個粒子，每個粒子都有自己的位置和速度，還有一個由被優化函數決定的適應值。每個粒子利用自身的記憶和從群體中獲得的信息更新自己的速度矢量和位置以追隨當前的2個“極值”，并通過群體中的信息共享來實現尋優搜索。這2個極值包括個體極值和全局極值，粒子本身所找到的最優解，叫做個體極值，整個種群目前找到的最優解，叫做全局極值。其計算流程如下:首先，在可行解內隨機初始化一定數量的粒子;然后，計算各個粒子的適應值、個體極值及全局極值，粒子可根據式(4)來更新自己的位置和速度，直到找到最優解，迭代終止。算法迭代終止條件一般為達到最大迭代次數或搜索到的最優位置的適應值滿足預定的最小適應度閾值。

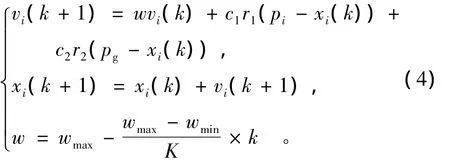
式中:vi(k)，vi(k+1)分別是第i個粒子在第k，k+1步迭代時的速度;xi(k)，xi(k+1)分別是第i個粒子在第k，k+1步迭代時的位置;pi為個體極值，表示第i個粒子經歷過的最好位置;pg為全局極值，表示所有粒子所經歷過的最好位置;c1，c2是常數，0＜c1＜c2＜2［4］;r1，r2是［0，1］區間均勻分布的隨機數;權重系數w隨算法迭代的進行而線性地減少為算法的總迭代次數。

4.2 改進粒子群算法

PSO在求解優化問題時存在粒子種群多樣性喪失迅速，難以收斂于全局最優等缺點。引入收縮因子χ和自適應變異算子對PSO進行改進［4－7］。

4.2.1 引入收縮因子

權重系數w對優化性能有很大的影響，w較大時算法具有較強的全局搜索能力，w較小時算法有利于局部搜索。w線性遞減只對某些問題有效，但對于不同的問題，其每次迭代所需要的比例關系并不相同，為此，引入收縮因子。該方法描述了一種選擇w，c1，c2值的方法，以確保算法收斂。通過正確選擇這些控制參數，就不必將 vi，j限制在［－vmax，vmax］中。帶有收縮因子的運動方程式如式(5)示:

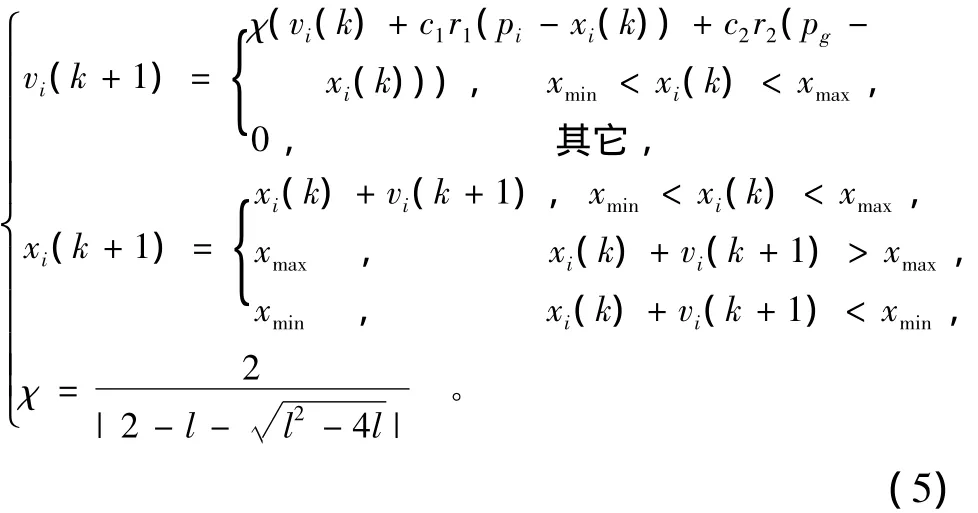
式中:c1=2.8，c2=1.3，l=c1+c2;微粒群規模 N=30;χ為收縮因子，其作用類似于參數vmax的作用。試驗結果表明，與vmax和w相比，χ更能有效地控制粒子的變化速度，具有更好的收斂性［4－5］。

4.2.2 引入變異算子

為克服PSO難以收斂于全局最優解的缺陷，在每個迭代階段內選擇一半粒子群進行變異，以防止算法陷入局部最優。變異方法如下:首先以適應值為判斷依據，對種群中所有個體進行由優到劣排序，選擇種群底部的一半個體作為被變異的粒子。然后對種群中頂部的一半個體進行基于遺傳思想的變異復制，并取代被變異的粒子，在此過程中全局極值并未改變。粒子變異運動方程如式(6)示

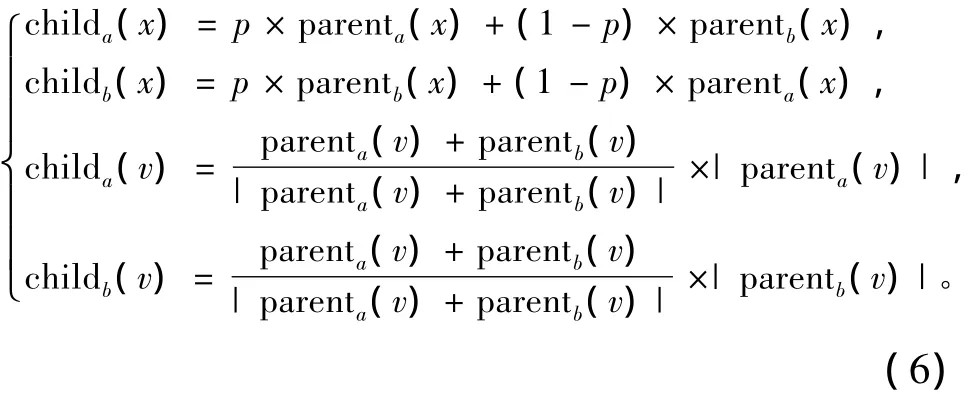
式中:x是D維位置向量元素;p是D維均勻分布的隨機數向量元素，其每個分量都在［0，1］內取值;v為D維速度向量元素。經過任意2個親代個體的雜交操作，隨機產生了2個新的位置，速率的交叉處將2個親代個體的速率之和的長度規格化，只有方向受到影響，數量沒有被影響，交叉操作繼承了雙親粒子的優點，加強了跳出局部最優的能力［4］。

5 算例分析

5.1 基礎數據

已有松江河各電站機組完好狀態、機組及電站動力特性數據、機組穩定性特性數據、各水庫庫容特性曲線、下游水位與流量關系曲線;已知計劃日的各水庫庫水位、水庫來水、電站區間來水、各電站實際運行數據及對電站運行方式的限制因素等。各電站優調方案的日初、末庫水位與實際運行相同，即日用水量相同。計劃日梯級電站模擬交易電價如圖1所示。

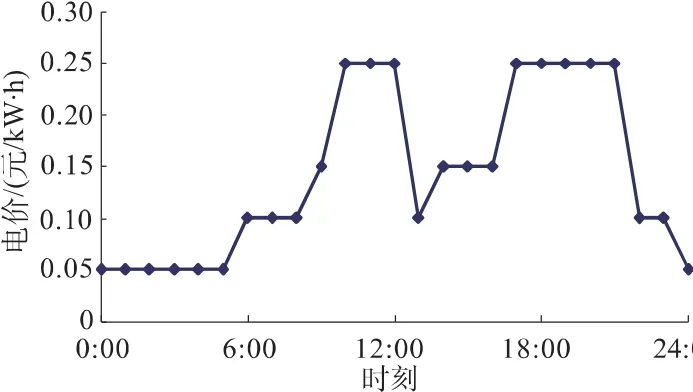
圖1 計劃日梯級水電站電價模擬圖Fig.1 Simulation of electricity price of cascade hydropower stations on scheming day

說明:當P≤0.85Pmax時，為低谷負荷和基荷，其電價定為0.05元/kW·h;當0.85Pmax＜P≤0.9Pmax時，為腰荷，其電價定為0.10元/kW·h;當0.9Pmax＜P≤0.94Pmax時，為腰荷，其電價定為0.15元/kW·h;當P ＞0.94Pmax時，為峰荷，其電價定為0.25元/kW·h。P為實時負荷，Pmax為最大負荷。

5.2 求解方法

應用改進粒子群算法求解該問題可表述為:找到一個最優粒子，即一種最優調度策略(各水庫水位Zi(t)的最優變化序列)，在滿足電網、水庫、電站及機組的多種約束條件下使梯級電站發電量(或發電效益)最大。求解步驟如下:

(1)設置粒子群規模(N=30)，初始化各粒子，確定各類限制條件和迭代終止判據。

(2)計算所有粒子的適應值，將各粒子的適應值暫時作為各粒子的個體極值，所有個體極值中最好的粒子作為全局極值。

(3)根據引入收縮因子的運動方程更新各個粒子的位置和速度。

(4)計算更新后各粒子的適應值，若更新后粒子的適應值優于該粒子當前個體極值或全局極值，則將更新的粒子作為該粒子的個體極值或全局極值。

(5)根據適應值優劣排序，引入變異算子進行交叉計算。

(6)檢驗是否滿足迭代終止條件，若滿足則迭代終止、輸出結果，否則轉到(4)繼續迭代，至到迭代終止。全局極值的位置即為梯級電站的最優調度參數。

5.3 計算結果及分析

5.3.1 日發電量最大方案

以日發電量最大為優化準則，計算在日用水量給定條件下的松江河梯級電站最優日運行方式，對30 d的運行數據進行優化計算，計算成果見表2。

通過分析可得出以下結論:①與實際運行方案相比，優調方案日發電量可增加2.88%～6.95%，在仿真計算的30 d中，共增發電量993.49萬kW·h，效益可觀;②優調方案具有先蓄水后發電的規律，計劃日初盡量少發電，將規定的日用水量放在接近日末的時段中用，可使水量在盡可能高的水頭下發電，優調方案符合直觀分析規律;③在某些天內石龍電站優調方案的發電量比實際發電量小，但梯級電站總發電量增加了，說明總體(水電站群)最優和局部(單個電站)最優并不完全一致;④在優調方案中存在石龍電站經常在日初第1時段發電，而雙溝電站在此時段及其后多個時段都不發電的＇怪現象＇。這是由于石龍電站為提高運行水頭，庫水位一直保持在正常最高值，雖然上庫無下泄流量，但還有區間流量入庫，在日初用發電方式按區間來水量大小騰空水庫，避免棄水，以增加發電量。

5.3.2 日發電效益最大方案

以日發電效益最大為優化準則，計算在日用水量給定條件下松江河梯級電站的最優日運行方式，對30 d的運行數據進行優化計算，計算成果見表3。

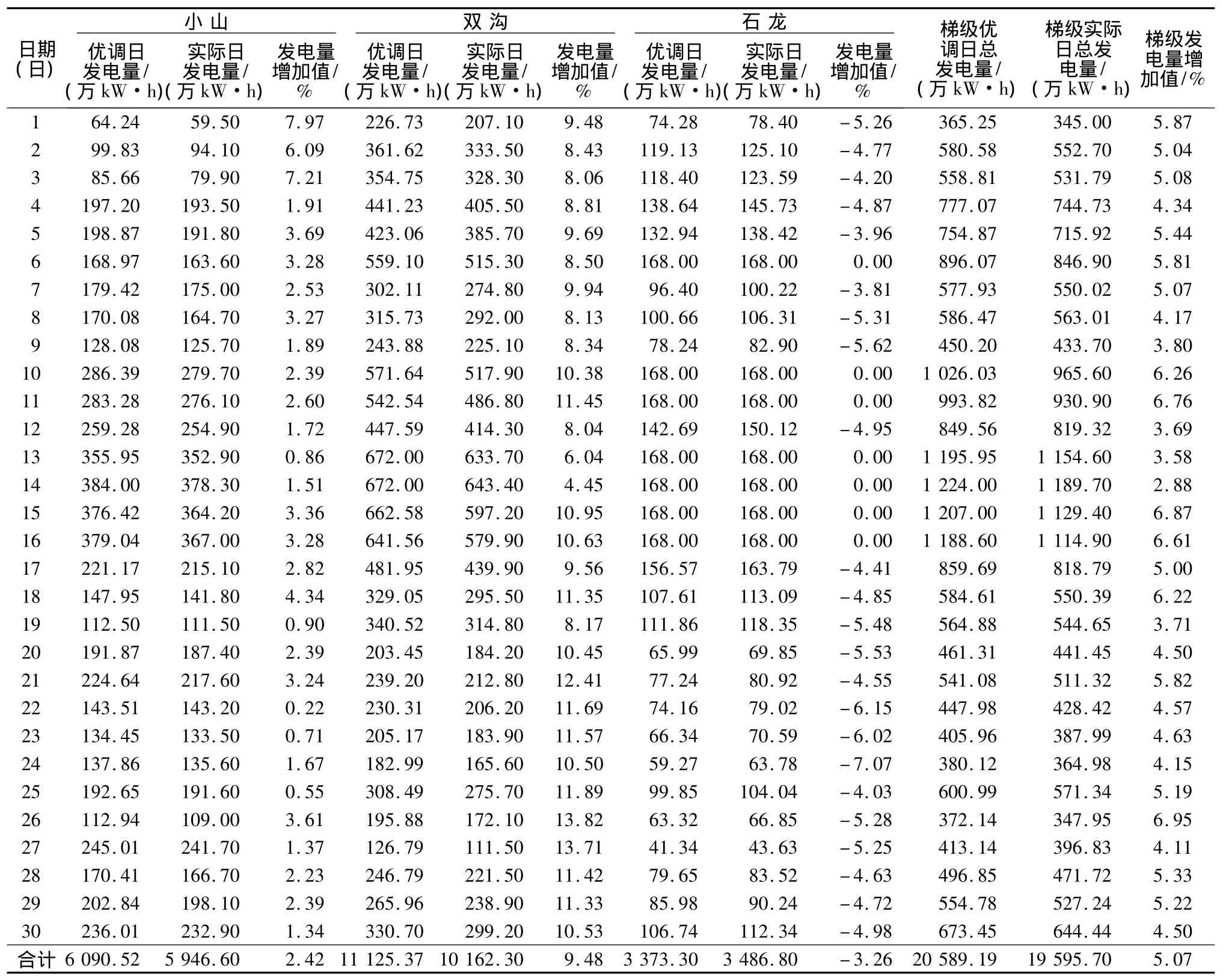
表2 松江河梯級電站發電量最大方案仿真計算成果Table 2 Optimal results of Songjianghe cascade hydropower stations calculated by maximizing power generation

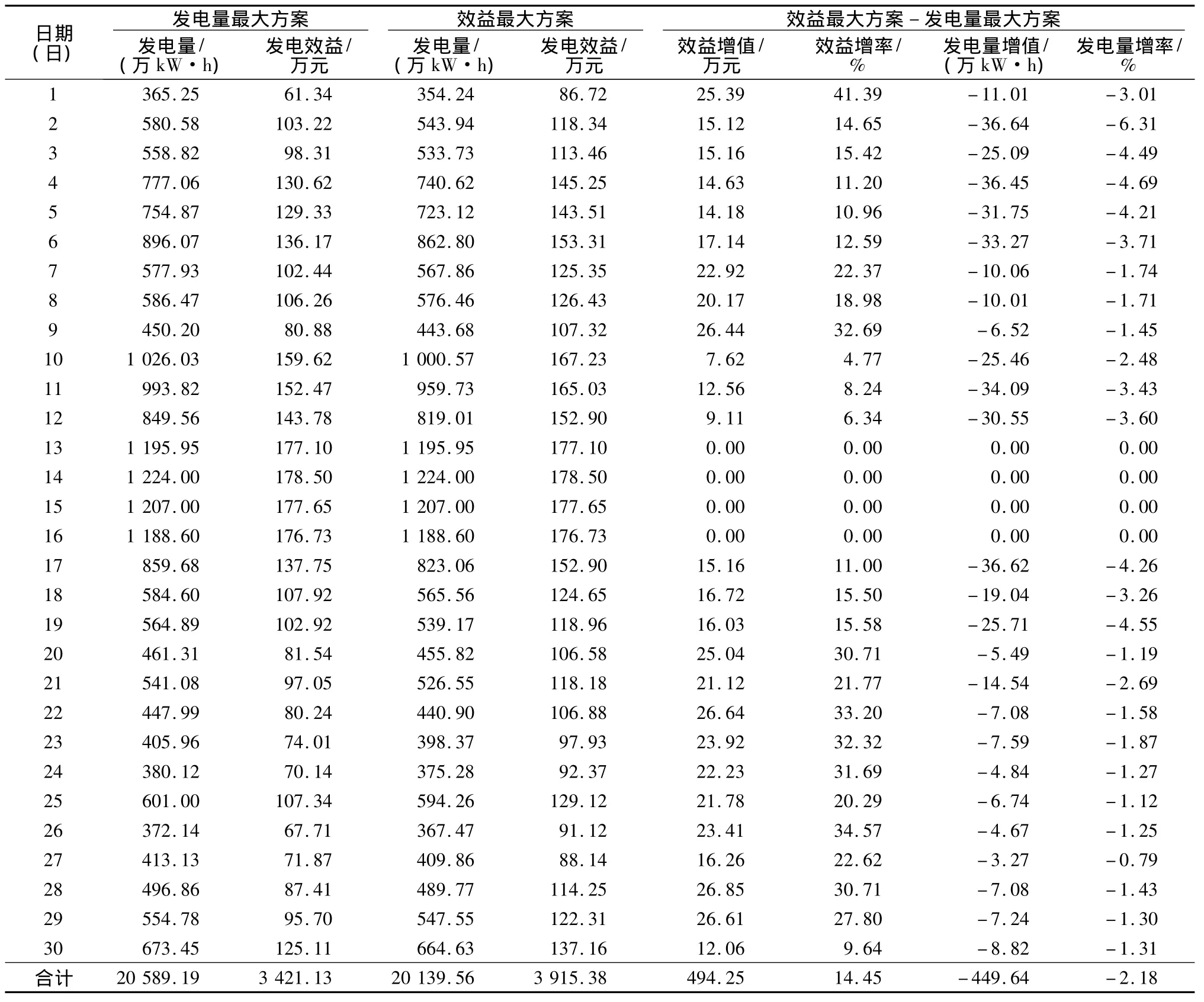
表3 松江河梯級電站發電效益最大方案仿真計算成果Table 3 Optimal results of Songjianghe cascade hydropower stations calculated by maximizing generation profit

通過分析可得出以下結論:①與發電量最大調度方案相比，經濟效益最大調度方案日均發電量減少14.99萬kW·h，但日均經濟收入增加16.48萬元，該方案除充分利用水頭增加發電量外，還考慮各時段間的電價差異，盡可能大地增加經濟收益。當用水量充裕時，可全時段以裝機容量發電，此時，這2種優化方案相同。②在日優調方案中，石龍電站存在在日初時段(低電價區)發電現象。雖然此時雙溝電站無下泄流量，但有區間入庫流量，石龍水庫日初已蓄滿，若不發電將棄水。但計劃日區間來水很小，只用本時段不蓄水量無法發電，故將水庫進行發電預泄，待蓄未來時段的區間入庫流量至雙溝電站開始發電下泄流量到達石龍水庫前蓄到期望水位。若區間來水較大，可將石龍水庫維持在高水位，直至雙溝電站開始發電下泄流量到達石龍水庫前才加大出力，迅速降至期望水位。③此次計算，發電量最大和經濟效益最大這2種優調方案比實際日發電量分別增加33.12萬kW·h和18.13萬kW·h，對梯級水電站進行短期優化調度可提高其整體質量和效益。

6 結論

隨著松江河梯級調度中心的逐漸形成和完善，研究松江河梯級水電站短期優化調度問題，對于把握梯級水電站的運行規律，提高梯級電站的整體質量和效益有重要意義。本文建立了發電量最大和發電效益最大梯級電站短期優化調度數學模型，并應用改進粒子群算法求解松江河梯級電站短期優化調度問題，對梯級水電站進行短期優化調度可以提高水能利用率及整個梯級電站的經濟效益。應用改進粒子群算法求解梯級水電站短期優化調度問題，無論求解精度、求解時間還是求解結果的合理性都取到了較滿意的結果。

［1］張高峰，權先璋，余 波，等.三峽梯級日優化運行模型及算法［J］.長江科學院院報，2003，20(3):10－12.(ZHANG Gao-feng，QUAN Xiang-zhang，YU Bo，et al.Optimal Daily Operation Model and Algorithm for Three Gorges Cascade Hydropower Plants［J］.Journal of Yangtze River Scientific Research Institute，2003，20(3):10－12.(in Chinese))

［2］吳杰康，郭壯志，秦礪寒，等.基于連續線性規劃的梯級水電站優化調度［J］.電網技術，2009，33(8):24－29.(WU Jie-kang，GUOZhuang-zhi，QIN Li-han，et al.Successive Linear Programming Based Optimal Scheduling of Cascade Hydropower Station［J］.Power System Technology，2009，33(8):24－29.(in Chinese))

［3］謝紅勝，吳相林，陳 陽，等.梯級水電站短期優化調度研究［J］.水力發電學報，2008，27(6):1－7.(XIE Hong-sheng，WU Xiang-lin，CHEN Yang，et al.Research on Short-term Optimization Operation of Cascade Hydropower Stations［J］.Journal of Hydroelectric Engineering，2008，27(6):1－7.(in Chinese))

［4］SUGANTHANPN.Particle Swarm Optimizer with Neighborhood Operator［C］∥Proceedings of the Congress on Evolutionary Computation.Washington D.C，July 06－09，1999.

［5］楊 維，李歧強.粒子群優化算法綜述［J］.中國工程科學，2004，6(5):87－94.(YANG Wei，LI Qi-qiang.Survey on Particle Swarm Optimization Algorithm［J］.Engineering Science，2004，6(5):87－94.(in Chinese))

［6］KENNEDY J，EBERHART R.Particle Swarm Optimization［C］∥Proceedings of the IEEE International Conference on Neural Networks.Perth，Australia.Nov.27－Dec.01，1995，4:1942－1948.

［7］馮雁敏，李承軍，張雪源.基于改進粒子群算法梯級水電站短期優化調度研究［J］.水力發電，2009，35(4):24－28.(FENG Yan-min，LI Cheng-jun，ZHANG Xueyuan.Research on the Short-term Optimal Scheduling of Cascade Hydropower Plants Based on Improved Particle Swarm Optimization［J］.Water Power，2009，35(4):24－28.(in Chinese))