基于路基面不均勻變形的路堤地基差異沉降限值研究

李 鐵，羅 強，王佳敏，陳 虎，劉瀟瀟

(西南交通大學高速鐵路線路工程教育部重點實驗室，成都 610031)

通常路基的沉降是由路堤本體的變形和路堤地基下沉引起的，但高速鐵路路堤是采用優質填料填筑的，而且壓實標準較高，一般變形較小，路基面的沉降主要由地基下沉引起［1］。所以高速鐵路路基變形控制中，主要限制路堤地基的下沉量，并以此來控制路基面的沉降。另外，為了保證高速列車的安全、平穩運行，線路必須具有高平順性。因此，需對高速鐵路路基的變形，尤其是路基的不均勻變形進行嚴格的控制。這無疑加大了路堤地基沉降，包括路堤地基不均勻沉降的控制難度。

本文直接從路堤地基的差異沉降出發，擬定了錯臺式和漸變式2種路堤地基差異沉降計算模型，圍繞著路基面不均勻變形和路堤地基差異沉降控制問題進行了討論。同時基于有限元軟件計算結果，找出了允許最大地基差異沉降值，這對解決路堤地基的差異沉降控制問題有一定意義。

1 路堤地基差異沉降計算模型

由于路堤地基的不均勻性和路堤地基處理方式不同，地基差異沉降的形式各有不同。本文主要考慮路堤地基差異沉降為漸變式和其極限情況——錯落式2種形式，同時參考文獻［2－3］擬定了2種路堤地基差異沉降計算模型。

1.1 路堤地基差異沉降模式及有限元計算模型

本文擬定的2種路堤地基差異沉降計算模型為錯臺式(錯落式)計算模型和線性漸變式(簡稱漸變式)計算模型。漸變式計算模型主要考慮沿線路縱向路堤地基差異沉降為漸變分布情況，即差異沉降值有一線性漸變段，為連續分布型，如圖1所示。錯臺式計算模型(地基差異沉降漸變段長l=0 m)主要考慮沿線路縱向路堤地基差異沉降為錯落式分布情況，即考慮漸變式模型的極限情況。

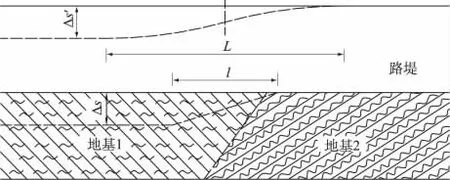
圖1 路堤地基差異沉降模式示意圖Fig.1 Differential settlement of the embankmentfoundation

1.2 計算條件和模型參數

考慮到我國高速鐵路路基的特點，計算中作了如下假定:①路堤部分為連續均勻、各向同性體，路堤各層采用Mohr-Coulomb材料模擬;②按平面問題計算，即認為路基橫向寬度范圍內沉降均勻，只在線路縱向存在差異沉降;③除模型本身受重力荷載外，模型只受位移荷載(模擬地基差異沉降)，由于軌道部分荷載不大，對模型變形影響不顯著，故不作考慮;④只考慮路堤地基差異沉降地段有限部分，且只考慮模型的垂向差異變形，不計其水平方向變形，故模型左右端只設水平向約束，垂向不設約束，如圖2所示。

計算模型長均為100m。錯臺式計算模型根據路堤高度h不同，分為3種;漸變式計算模型根據地基差異沉降漸變段長度l和路堤高度h不同，分為9種，具體計算方案見表1。路堤部分材料參數見表2。其中，基床表層厚度取為0.4 m，基床底層厚度取為2.3 m［4］，材料剪脹角取為0.95φ，φ為內摩擦角。數值計算采用ABAQUS有限元軟件進行。

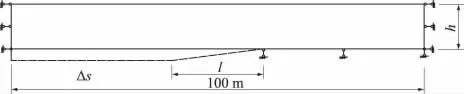
圖2 有限元計算模型示意圖(漸變式)Fig.2 Finite element model

表1 模型計算方案Table 1 Numerical simulation schemes

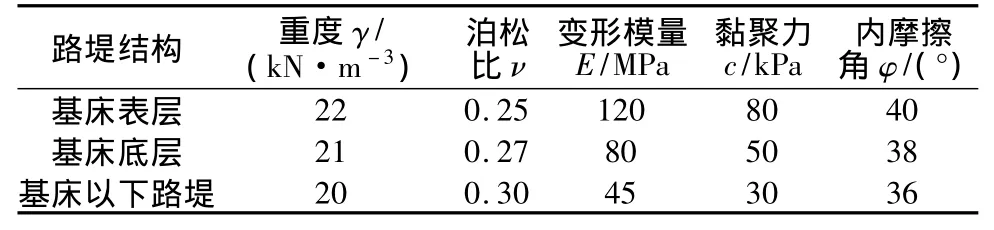
表2 路堤填料計算參數Table 2 Parameters of embankment fillings

2 路堤地基差異沉降影響分析

2.1 不均勻變形斜率

路基面的不均勻變形斜率(簡稱不均勻變形斜率)指路基面不均勻變形曲線上相鄰2點之間對應的割線斜率，即路基面上2點之間的不均勻變形縱坡坡度，用k表示，其最大值kmax，簡稱為最大不均勻變形斜率。有限元計算結果表明:在地基差異沉降為小變形情況下，2種模型的路基面不均勻變形曲線均呈“S”形，和文獻［2］中相似，如圖3所示。該曲線的最大特點是中間存在斜率最大的拐點C，從C點向左右兩側，斜率逐漸減小。因此，可利用路基面不均勻變形曲線的最大斜率來代表路基面的不均勻變形程度。此處所指的路基面不均勻變形曲線斜率和文獻［5］中提及的“切線坡度”(切線斜率)相似。

2.1.1 路基面不均勻變形曲線特征

斜率分為切線斜率和割線斜率，割線斜率的表達式見式(1)，其中Δx，Δy為曲線上任意2點之間的橫、縱坐標增量值。當Δx→0時，極限k=為切線斜率，其表示曲線對應的函數在某點的導數值。

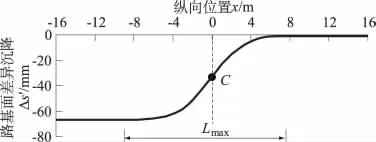
圖3 路基面不均勻變形曲線示意圖Fig.3 Curve of uneven deformation of subgrade surface

將路基面不均勻變形曲線上鄰近2點I(xi，yi)和J(xj，yj)的割線斜率kij(即不均勻變形斜率)近似等效為該曲線的切線斜率，并以此來近似確定其特征點C位置。

由式(1)可得

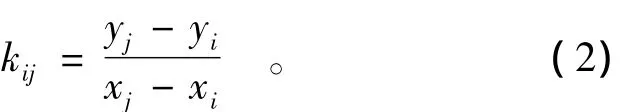
式(2)對應的物理意義為路基面上I和J這2點之間的不均勻變形縱坡坡度值。

2.1.2 路基面不均勻變形斜率限值

目前國內外高速鐵路不平順控制指標多為軌面折角限值θ。本文近似取路基面不均勻變形斜率限值m為相應的軌面折角限值θ;由于線路縱向呈長條型分布，在大范圍內軌面和路基面不均勻變形基本一致，所以當路堤地基差異沉降分布范圍較大時這樣取值是合理的。對于高速鐵路，當線路標準不同(行車速度V不同)時，軌面折角θ的取值是不同的。文獻［6］建議:V=250km/h時，θ可取3/1 000;V=350km/h時，θ可取2/1 000。文獻［1，7］則指出:行車速度V為250，350km/h時，θ應控制在3/1 000，1.5/1 000范圍內。而我國現行規范規定:對于無砟軌道高速鐵路，不均勻沉降造成的折角應不大于1/1 000［4］。

參考相關文獻，折角限值取為:V=250km/h時，m=3/1 000;V=300km/h 時，m=2/1 000;V=350km/h時，m=1/1 000。

2.2 有限元計算數據分析

經過分析發現，當計算模型路堤高度h、地基差異沉降漸變段長度l固定時，路基面最大不均勻變形斜率kmax隨地基差異沉降Δs增加而增加，且在地基差異沉降較小時幾乎呈線性增加趨勢。如圖4所示。

圖4(a)為路堤高度h=6 m，地基差異沉降漸變段長度l分別為0，4，8，12 m 時，kmax-Δs變化曲線。圖4(b)為地基差異沉降漸變段長度l=0 m及l=8 m，路堤高度h分別為3，6，9 m 時，kmax-Δs變化曲線。

當路堤高度h，地基差異沉降Δs不變時，路基面的最大不均勻變形斜率kmax隨地基差異沉降漸變段長度l的增加而減小;地基差異沉降漸變段長度l=0 m時，kmax最大;這說明在路堤底部增設地基差異沉降漸變段有利于減緩路基面的不均勻變形縱坡坡度，即減小地基差異沉降對路基面的擾動程度，且l越長對減緩路基面的不均勻變形縱坡坡度越有利，如圖5(a)所示。當地基差異沉降漸變段長度l，地基差異沉降 Δs不變，且l＜(3.5～3.7)h時，路基面變形曲線的最大不均勻變形斜率kmax隨路堤高度h的增加而減小，這說明同一地基差異沉降下，路堤越高，路基面的不均勻變形縱坡坡度越緩，地基差異沉降對路基面的擾動程度越小，如圖5(b)所示。

圖4 k max-Δs曲線Fig.4 Curves of k max-Δs

3 路堤地基差異沉降控制標準

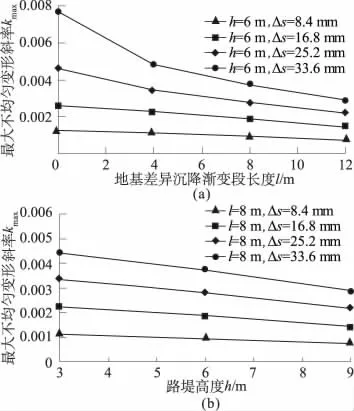
圖5 k max-l與k max-h曲線Fig.5 Curves of k max-l and k max-h

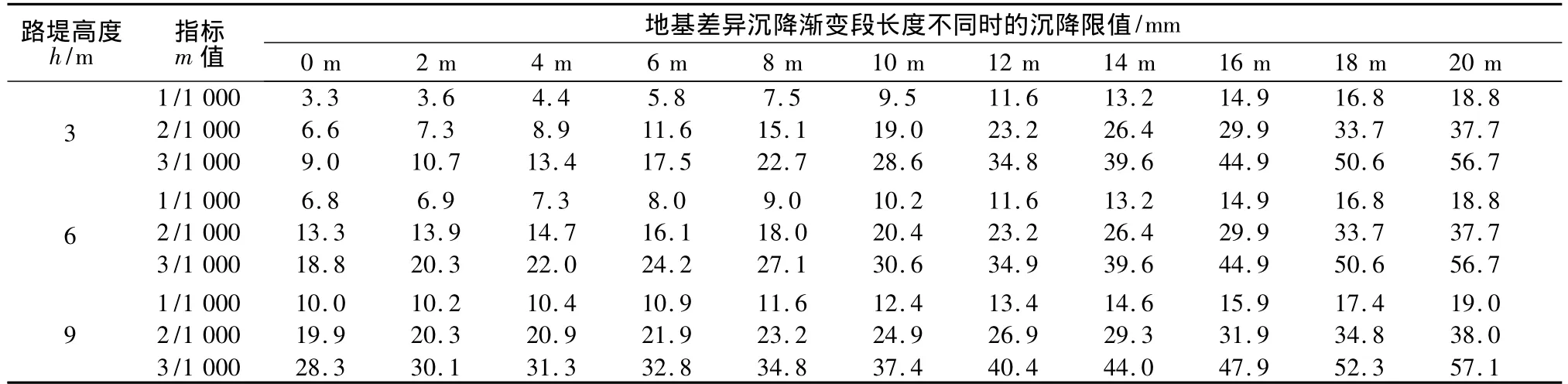
表3 路堤地基差異沉降限值［Δs］Table 3 Limit values of embankment foundation differential settlement［Δs］

計算中發現，當地基差異沉降很小時，路基面最大不均勻變形斜率kmax小于給定的指標m，此時地基差異沉降對路基面的擾動可忽略不計。由不均勻變形斜率變化規律可知，對于一種模型，一定存在著某一地基差異沉降限值［Δs］，使路基面的最大不均勻變形斜率剛好等于m，此時的地基差異沉降值，即為地基差異沉降臨界值，其對應的是路堤底部地基的差異沉降限值。

表3列出了不同標準下各模型對應的路堤地基差異沉降限值［Δs］。從中可看出，當路堤高度h和地基差異沉降漸變段長度l一定時，地基差異沉降限值［Δs］隨指標m的增加呈增加趨勢;當l≥4 m時，地基差異沉降限值［Δs］隨指標m的增加，呈線性增加趨勢，且近似成倍數關系。當指標m相同，路堤高度h一定時，地基差異沉降限值［Δs］隨地基差異沉降漸變段長度l的增加而呈非線性趨勢增加，且增加幅度逐漸增大，最后增加趨勢趨于線性，其中l=0 m 時，［Δs］最小，其值可用式［Δs］min=0.548m0.924/h－1.02(h 單位取mm)近似計算，如圖6(a)所示及表3所列。這說明了路堤高度h一定時，增加地基差異沉降漸變段長度可有效提高地基差異沉降限值，且地基差異沉降漸變段越長，效果越明顯。當指標m相同，地基差異沉降漸變段長度l一定時，地基差異沉降限值［Δs］隨路堤高度的變化規律跟l有關，當l較小時，差異沉降限值［Δs］隨路堤高度h的增加而增加;但l大于一定程度時，差異沉降限值［Δs］不再隨路堤高度h的增加而增加，如圖6(b)所示。計算數據表明:當地基差異沉降漸變段長度l大約為路堤高度h的2～2.5倍時，開始出現地基差異沉降限值［Δs］不再隨路堤高度h的增加而增加的情況，此時［Δs］主要受l的影響。

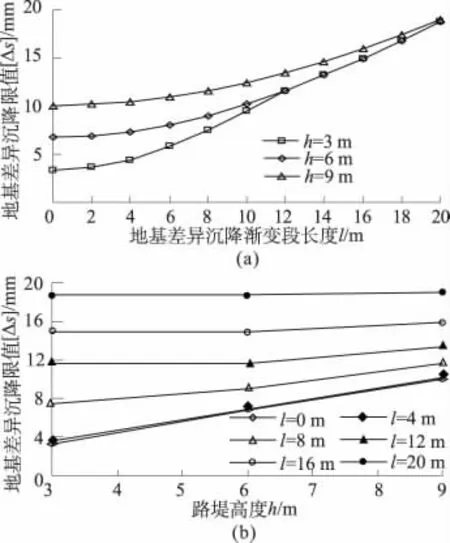
圖6 ［Δs］-l和［Δs］-h曲線Fig.6 Curves of［Δs］-l and［Δs］-h

4 土工離心模型試驗驗證

本文提取了西南交通大學陳虎等人相應的土工離心模型試驗部分數據，分別對錯臺式和漸變式6種計算模型共24組數據進行了比較，部分對比結果如圖7所示。

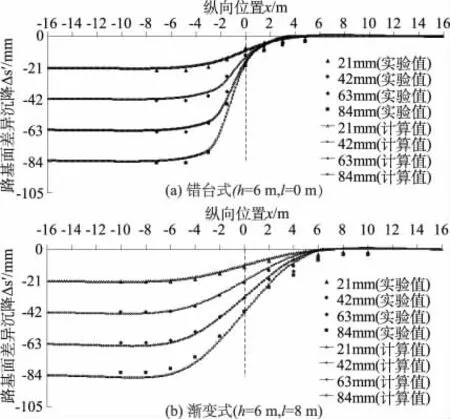
圖7 土工離心模型試驗數據與有限元計算數據對比Fig.7 Comparison between centrifugal data and FEM data

表4列出了有限元計算數據和土工離心試驗數據的差異情況，其中R2為相關指數［8］，其計算公式為

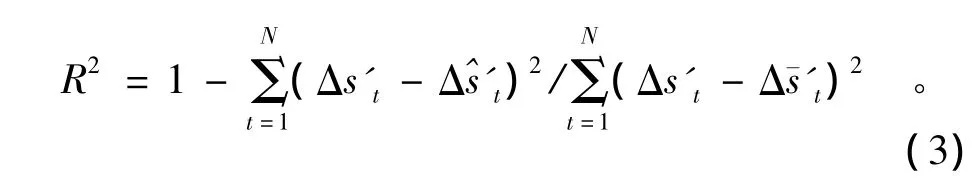
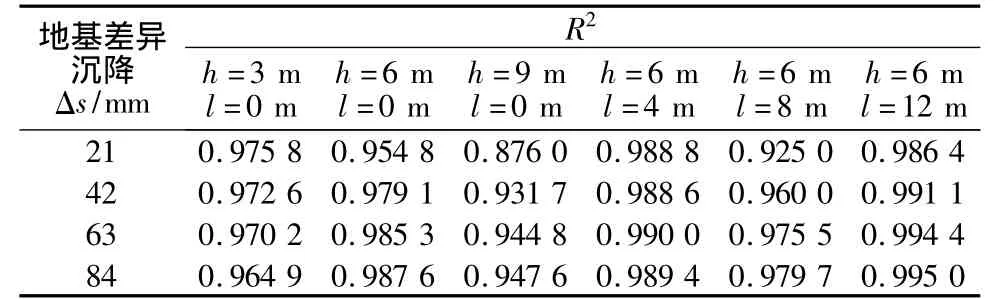
表4 有限元計算數據與土工離心試驗數據差異Table 4 Differences between FEM data and centrifugal data

如表4所列，有限元計算數據與土工離心試驗數據普遍吻合較好，只有路堤高9 m時錯臺式模型計算數據與土工離心實驗數據相差相對大一些。

5 結語

通過對地基差異沉降模式進行簡化，建立了錯臺式和漸變式2種路堤地基差異沉降計算模型，給出了路基面不均勻變形斜率k的計算方法及基于路基面不均勻變形的路堤地基差異沉降限值［Δs］的計算方法，最后采用土工離心模型試驗結果對有限元計算數據進行了驗證。

在給定計算參數條件下，通過計算及分析表明:

(1)路堤高度h和地基差異沉降漸變段長度l均會影響地基差異沉降對路基面的擾動程度，即路基面不均勻變形程度。

(2)地基差異沉降限值［Δs］同樣受路堤高度h和地基差異沉降漸變段長度l的影響，對于不同的路基，［Δs］一般不同。當路堤地基差異沉降為錯落式分布時，對應的地基差異沉降限值［Δs］最小，為最不利情況，其值可近似用下式計算，

對于一定高度路堤，增加地基差異沉降漸變段能有效增大地基差異沉降的允許值，且地基差異沉降漸變段越長效果越好。

(3)當路堤地基差異沉降漸變段長度l大于路堤高度h的2～2.5倍時，可忽略路堤高度對地基差異沉降限值［Δs］的影響。

［1］羅 強.高速鐵路路橋過渡段動力學特性分析及工程試驗研究［D］.成都:西南交通大學，2003:99，164.(LUO Qiang.Dynamic Performance Analyses and Experiment Study on Bridge/Approach Embankment of High-Speed Railway［D］.Chengdu:Southwest Jiaotong University，2003:99，164.(in Chinese))

［2］羊 曄，劉松玉，鄧永鋒，等.軟土地基過渡段差異沉降控制標準［J］.東南大學學報，2008，38(5):834－838.(YANG Ye，LIU Song-yu，DENG Yong-feng，et al.Differential Settlement Controlling Criteria of Highway Transition Sections on Soft Soil Foundation［J］.Journal of Southeast University，2008，38(5):834－838.(in Chinese))

［3］陶向華.路橋過渡段差異沉降控制標準與人車路相互作用［D］.南京:東南大學，2006:8－9.(TAO Xiang-hua.Differential Settlement Control Criterion of Bridge-Approach and People-Vehicle-Road Interaction［D］.Nanjing:Southeast University，2006:8－9.(in Chinese))

［4］TB10621－2009，高速鐵路設計規范(試行)［S］.北京:中國鐵道出版社，2010.(TB10621－2009.Code for Design of High Speed Railway(Trial)［S］.Beijing:China Railway Publishing House，2010.(in Chinese))

［5］劉萌成.橋臺后回填差異沉降控制標準及設計方法研究［D］.南京:東南大學，2005:40－47.(LIU Meng-cheng.Investigation of the Design Criterion of the Bridge Approach Settlement for the Backfills［D］.Nanjing:Southeast University，2005:40－47.(in Chinese))

［6］王其昌，蔡成標，羅 強，等.高速鐵路路橋過渡段軌道折角限值的分析［J］.鐵道學報，1998，20(3):109－113.(WANG Qi-chang，CAI Cheng-biao，LUO Qiang，et al.Allowable Values of Track Deflection Angles on High Speed Railway Bridge-Subgrade Transition Sections［J］.Journal of the China Railway Society，1998，20(3):109－113.(in Chinese))

［7］陳善雄，宋 劍，周全能，等.高速鐵路沉降變形觀測評估理論與實踐［M］.北京:中國鐵道出版社，2010:72－75.(CHEN Shan-xiong，SONG Jian，ZHOU Quan-neng，et al.Theory and Practice of Settlement Deformation Observation and Evaluation for High-Speed Railway［M］.Beijing:China Railway Publishing House，2010:72－75.(in Chinese))

［8］費業泰.誤差理論與數據處理(第六版)［M］.北京:機械工業出版社，2010:149－150.(FEI Ye-tai.Error Theory and Data Processing(the Sixth Edition)［M］.Beijing:China Machine Press，2010:149－150.(in Chinese))