三峽水庫運用初期庫區水沙輸移數值模擬

黃仁勇，李 飛，張細兵

(1.長江科學院河流研究所，武漢 430010;2.長江水利委員會規劃計劃局，武漢 430010)

1 研究背景

泥沙問題是三峽工程中的關鍵技術問題之一。在三峽工程泥沙問題研究過程中，我國主要采取原型觀測分析與調查、數學模型計算和實體模型試驗相結合的研究方法，取得了許多研究成果，也推動了整個泥沙學科的發展。同時，泥沙數學模型也在廣泛應用中不斷取得新的進展，其中長江科學院和中國水利水電科學研究院以一維不平衡輸沙理論為基礎建立的三峽水庫一維水沙數學模型，已成為目前比較成熟的數學模型，并在三峽工程泥沙研究中起到了基礎和關鍵性作用［1］。

三峽水庫庫長700余km，區間支流眾多，各支流的入庫水量和庫容也較大，為提高水庫調蓄計算的精度，有必要將更多支流納入計算范圍;而以往研究均沒有進行庫區小支流的水沙輸移計算，對區間支流庫容及來水影響考慮不夠。本文考慮水沙輸移過程中的非恒定性，建立了三峽水庫一維非恒定水沙數學模型，該模型為一樹狀河網模型，可以將更多支流納入水沙輸移計算范圍。

自2003年6月三峽水庫投入運用以來，三峽庫區的沖淤特點發生了明顯變化，庫區河道由整體上的沖淤基本平衡轉向持續淤積狀態，為準確了解三峽庫區水流及河床在水庫運行后的變化規律，長江水利委員會水文局對三峽水庫蓄水后水沙資料進行了詳細觀測，這為數學模型驗證與改進提供了寶貴的資料。本次驗證選用三峽水庫運用后2003年6月至2009年12月實測水沙資料，檢驗模型對庫區洪水演進過程、沿程水位變化過程及河床沖淤演變過程的模擬精度，分析模型預測計算結果的可信度，為今后模型的改進與應用提供新的依據。

2 數學模型的建立

三峽庫區支流眾多，建立三峽水庫一維非恒定水沙數學模型應同時考慮干支流水沙運動，將水庫干支流河道分別視為單一河道，河道匯流點稱為汊點，則水沙數學模型應包括單一河道水沙運動方程、汊點連接方程和邊界條件3部分［2］。

2.1 單一河道水沙運動方程

(1)模型選用的描述單一河道水流與泥沙運動的基本方程為［3］:

水流連續方程

水流運動方程

泥沙連續方程

河床變形方程

式中:ω為泥沙沉速;角標i為斷面號;Q為流量;A為過水面積;t為時間;x為沿流程坐標;Z為水位;K為斷面流量模數;S為含沙量;S*為水流挾沙力;ρ'為淤積物干密度;B為斷面寬度;g為重力加速度;α為恢復飽和系數;Ad為河床沖淤面積。

2.2 汊點連接方程

2.2.1 流量銜接條件

進出每一汊點的流量必須與該汊點內實際水量的增減率相平衡，即

式中Ω為汊點的蓄水量。如將該點概化為一個幾何點，則Ω=0。

2.2.2 動力銜接條件

如果汊點可以概化為一個幾何點，出入各個汊道的水流平緩，不存在水位突變的情況，則各汊道斷面的水位應相等，即

2.3 邊界條件

計算中不對某單一河道單獨給邊界條件，而是將納入計算范圍的三峽水庫干支流河道作為一個整體給出邊界條件，各干支流進口給流量和含沙量過程，模型出口給水位過程、流量過程或水位流量關系。

2.4 有關問題的處理

2.4.1 床沙交換及級配調整

關于床沙交換及級配調整，本模型采用3層模式，即把河床淤積物概化為表、中、底3層，表層為泥沙的交換層，中間層為過渡層，底層為泥沙沖刷極限層。規定在每一計算時段內，各層間的界面都固定不變，泥沙交換限制在表層內進行，中層和底層暫時不受影響。在時段末，根據床面的沖刷或淤積向下或向上輸送表層和中層級配，但這2層的厚度不變，底層厚度隨沖淤厚度的變化而變化。

2.4.2 水流挾沙力計算

水流挾沙力公式為［4］:

式中:S*為水流總挾沙力;u為平均流速;h為水深;ωm為非均勻沙平均沉速;pL為第L組泥沙的級配;ωL為第L組泥沙的沉速;k為挾沙力系數，水庫為0.03，天然河道為0.02。

2.4.3 恢復飽和系數α

恢復飽和系數是泥沙數學模型計算的重要參數，是一個綜合系數，需要由實測資料反求。但是影響因素很多，既與水流條件有關，又與泥沙條件有關，隨時隨地都在變化，在大多數泥沙沖淤計算中都假定為一正的常數，通過驗證資料逐步調整。本模型對泥沙沖淤采用分粒徑組算法，如果對各粒徑組都取同樣的α值，由于各組間的沉速相差可達幾倍甚至幾百倍，因而從計算結果看，在同一斷面上小粒徑組相對于大粒徑組來說其沖淤量常常可忽略不計，這往往與實際不盡相符。從三峽水庫蓄水運用以來進出庫的各粒徑組泥沙實測資料來看，各粒徑組泥沙的沿程分選現象均非常突出。目前對恢復飽和系數α取值的研究非常多，基本上有如下共識:①不同粒徑組泥沙的恢復飽和系數值不同;②恢復飽和系數取值應隨泥沙粒徑的增大而減小;③恢復飽和系數值應隨空間和時間而變化。為此本模型在計算中對不同粒徑組的恢復飽和系數αL采用如下經驗公式計算:

2.4.4 節點分沙

進出節點各河段的泥沙分配，主要由各河段臨近節點斷面的邊界條件決定，并受上游來沙條件的影響。本模型采用分沙比等于分流比的模式，即

3 數學模型求解

3.1 水流方程求解

可采用三級解法對水流方程進行求解，首先對水流方程(1)和(2)采用普列斯曼的四點隱式差分格式進行離散［5］，可得差分方程如下:

式中系數均按實際條件推導得出。

假設某河段中有m個斷面，將該河段中通過差分得到的微段方程(12)和(13)依次進行自相消元，再通過遞推關系式將未知數集中到汊點處，即可得到該河段首尾斷面的水位流量關系:

式中系數α1，β1，δ1，θm，ηm，γm由遞推公式求解得出。

將邊界條件和各河段首尾斷面的水位流量關系帶入汊點連接方程，就可以建立起以三峽水庫干支流河道各汊點水位為未知量的代數方程組，求解此方程組得各汊點水位，逐步回代可得到河段端點流量以及各河段內部的水位流量。

3.2 泥沙方程求解

對泥沙連續方程(3)用顯格式離散得

對河床變形方程(4)進行離散得

其中，Δt為時段;Δx為兩斷面間距。在求出干支流河道所有斷面的水位流量后，即可根據式(16)自上而下依次推求各斷面含沙量，汊點分沙計算采用分沙比等于分流比的模式，最后根據式(17)進行河床變形計算。

4 數學模型驗證

4.1 計算條件

計算范圍為干流朱沱－三峽壩址(見圖1)，長約760km。考慮嘉陵江、烏江、綦江、木洞河、大洪河、龍溪河、渠溪河、龍河、小江(支流小江又包含南河、東河、普里河、彭河等支流)、梅溪河、大寧河、沿渡河、清港河、香溪河共14條支流。起始計算地形中朱沱－李渡為1996年實測地形，李渡－三峽壩址為2003年蓄水前實測地形。計算進口采用干流朱沱站、嘉陵江北碚站、烏江武隆站3站2003年6月1日至2009年12月31日逐日平均流量和含沙量。出口采用廟河站相應時段逐日平均水位。區間來流量在計算河段內分配到入匯支流上，沒有考慮區間來沙。

4.2 水位及流量驗證

根據現有實測資料，選用沿程各主要水文站的2003－2004年實測水位流量過程與模型的計算結果進行了比較，結果見圖2和圖3，表1為三峽水庫2004年庫區部分測站最高洪水位值驗證結果。由圖表可見，模型計算的沿程各水文站洪水演進傳播過程及水位變化過程與實測情況基本一致，最高洪峰水位的出現計算值與實測值幾乎同步，模型驗證結果與實測值符合較好。

表1 2004年三峽庫區部分測站最高洪水位驗證Table 1 Verification of the highest flood level at stations in the TGR area in 2004

4.3 干流水文站輸沙量驗證

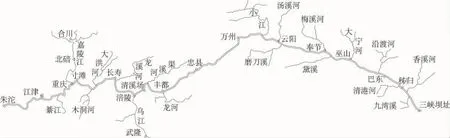
圖1 三峽水庫庫區干支流示意圖Fig.1 Schematic diagram of the mainstream and tributaries in the TGR area

圖4為三峽庫區部分主要水文站2003－2004年含沙量過程驗證結果，各站計算結果與實測值基本一致，但計算含沙量峰值比實測值小，而中小流量時計算值又稍有偏大，由于多數時期計算值與實測值相近，互有大小，所以全年累積輸沙量與實測值還是比較接近的(見表2)。

圖2 部分測站水位過程驗證Fig.2 Verification of water level history at three stations

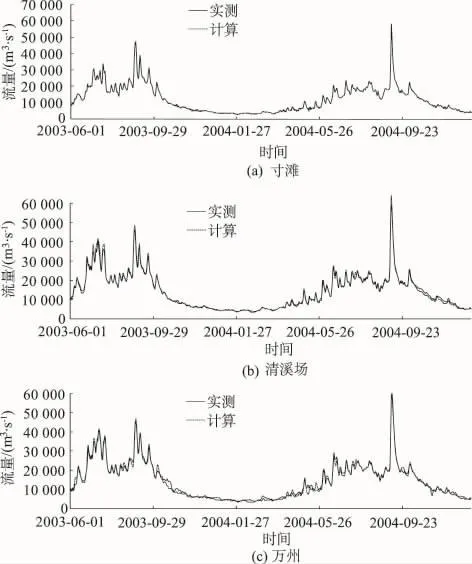
圖3 部分測站流量過程驗證圖Fig.3 Verification of water discharge history at three stations

圖4 部分測站含沙量過程驗證Fig.4 Verification of sediment concentration history at four stations

表2 主要測站輸沙量驗證Table 2 Verification of sediment discharge of some major stations 億t

4.4 淤積量及排沙比驗證

表3和表4分別為三峽庫區淤積量和排沙比驗證結果，從淤積過程、淤積分布及排沙比計算結果看，模型計算值與實測值均吻合較好。以朱沱至壩址為庫區淤積統計范圍，按輸沙量法統計，水庫運用至2009年底，朱沱至清溪場段、清溪場至壩址段及全庫區分別淤積1.392，9.773，11.18億t，與相應實測值1.631，9.338，10.97億t接近。從累積淤積量看，模型全庫段累積淤積量計算值與實測值相對誤差為1.9%。從排沙比驗證結果看，模型累積排沙比計算值與實測值相差約1.4%，且對排沙比較大(如2005年)和較小(如2006年)的年份均取得了較為滿意的驗證效果。

表3 淤積量及分布計算結果Table 3 Calculated results of deposition volume and its distribution

表4 排沙比計算值與實測值對比Table 4 Comparison between the calculated results and observed data of discharged sediment ratio

5 結論

鑒于以往研究中的三峽水庫水沙數學模型對庫區支流影響考慮不夠的現狀，本文考慮水沙輸移過程中的非恒定性及庫區更多支流庫容的影響，基于三級解法的基本思想，建立了三峽水庫一維非恒定水沙數學模型，提高了水沙計算精度;采用三峽水庫蓄水運用后2003－2009年實測資料對模型進行了驗證，計算的水位流量過程、輸沙量及排沙比等與實測值符合較好。驗證結果表明，此模型在非恒定輸沙計算方面有較好的精度，模型對三峽水庫水沙輸移及泥沙沖淤模擬計算基本合適，該模型可為三峽水庫沖淤預測和優化調度研究提供技術支持。

［1］彭 楊，張紅武.三峽庫區非恒定一維水沙數值模擬［J］.水動力學研究與進展，2006，21(3):285－292.(PENG Yang，ZHANG Hong-wu.1-D Numerical Simulation of Unsteady Flow and Sedimentation Transport at the Three Gorges Reservoir(TGR)［J］.Journal of Hydrodynamics，2006，21(3):285－292.(in Chinese))

［2］黃仁勇，黃 悅.三峽水庫干支流河道一維非恒定水沙數學模型初步研究［J］.長江科學院院報，2009，26(2):9－13.(HUANGRen-yong，HUANGYue.Preliminary Study on 1-D Numerical Simulation of Unsteady Flow and Sediment Transport in Mainstream and Tributaries of Three Gorges Reservoir Area［J］.Journal of Yangtze River Scientific Research Institute，2009，26(2):9－13.(in Chinese))

［3］謝鑒衡.河流模擬［M］.北京:中國水利水電出版社，1988:111－116.(XIE Jian-heng.River Simulation［M］.Beijing:China Water Power Press，1988:111－116.(in Chinese))

［4］張瑞瑾.河流泥沙動力學［M］.北京:中國水利水電出版社，1998:181－190.(ZHANG Rui-jin.River Sediment Dynamics［M］.Beijing:China Water Power Press，1998:181－190.(in Chinese))

［5］董耀華，黃煜齡.天然河道長河段一維非恒定流數模研究［J］.長江科學院院報，1994，11(2):10－17.(DONG Yao-hua，HUANG Yu-ling. A Mathematical Model of One-Dimensional Unsteady Flow in Long-Distance Natural Channel［J］.Journal of Yangtze River Scientific Research Institute，1994，11(2):10－17.(in Chinese ))