自適應混沌粒子群算法在PSS設計中的應用

陳 剛，簡華陽，龔 嘯

(輸配電裝備及系統安全與新技術國家重點實驗室(重慶大學電氣工程學院)，重慶 400044)

自適應混沌粒子群算法在PSS設計中的應用

陳 剛，簡華陽，龔 嘯

(輸配電裝備及系統安全與新技術國家重點實驗室(重慶大學電氣工程學院)，重慶 400044)

該文采用一種改進的粒子群算法PSO——自適應混沌粒子群算法ACPSO，對多機電力系統穩定器參數進行優化設計，以抑制系統低頻振蕩。該算法通過混沌初始化粒子群，在迭代計算過程中根據粒子的適應值自適應地調整算法慣性系數，從而可以獲得更好的全局搜索能力和收斂速度。選取系統機電振蕩模式最小阻尼比最大化為目標函數，將PSS參數優化轉換為帶不等式約束的非線性優化問題。以3機9節點系統為例，特征值和非線性仿真結果表明，運用該方法設計的PSS能夠有效地抑制外界擾動引起的低頻振蕩。

多機電力系統；電力系統穩定器；自適應混沌粒子群優化算法；低頻振蕩；電力系統穩定

隨著現代電力系統規模的擴大和負荷需求的日益增加，以及長距離、大容量輸電技術的發展，暫態穩定和動態穩定已成為影響電力系統是否可靠、有效運行的最重要考慮之一。伴隨高增益快速勵磁系統的廣泛應用，發電機電壓調節特性和電力系統的暫態穩定水平得到穩步提高。受此影響，系統對振蕩的阻尼作用可能受到削弱，從而在小擾動作用下易引發低頻振蕩，在弱互聯系統中顯得尤為顯著，嚴重時會導致系統解裂或失去安全穩定。同時，低頻振蕩也嚴重制約了聯絡輸電線的輸電能力。因此，如何提高系統阻尼水平，對改善系統的整體暫態和動態穩定性具有重要意義。

電力系統穩定器PSS作為改善電力系統穩定的措施之一，因其簡單、經濟和靈活的特點被廣泛應用。作為一種發電機附加勵磁控制裝置，PSS通過向發電機勵磁系統引入輔助信號向系統提供附加阻尼，以此增強系統的穩定性。

盡管利用現代控制技術可設計出更多不同結構的PSS，但電力工業中常用的依然是傳統的超前-滯后補償結構[1，2]。究其原因，主要是考慮其參數便于調整，而利用自適應或是變結構技術設計的PSS在實際使用過程缺乏足夠的可靠性以及維護調試的不便。在結構確定的基礎上，傳統PSS的設計主要問題即為PSS參數的選擇。電力系統的PSS參數優化問題大多可歸結為帶參數約束的非線性優化問題，優化過程較復雜。多年來，國內學者在這方面進行了大量的研究工作。最早用于優化PSS的線性規化方法、非線性優化方法對初始解的要求非常高，常常得到局部最優解，屬于局部尋優方法。為克服上述方法對初始猜測解的依賴，求取滿意的全局最優解，現代全局優化方法如禁忌搜索TS(tabu search)、遺傳算法GA(genetic algorithm)、模擬退火SA(simulated annealing)、遺傳禁忌GATS(genetic algorithm tabu search)等逐漸被用于PSS參數優化問題中[3～6]。除GA外，進化規劃EP(evolutionary programming)、進化策略等進化算法也均被用于PSS參數優化問題[7，8]。

粒子群優化PSO算法是美國Kennedy和Eberhart博士于1995年在模擬鳥群覓食過程中的遷徙和群集行為時提出的一種基于群體智能的演化計算技術 。其思想是：將群體中的每個個體視為多維搜索空間中一個沒有質量和體積的粒子(點)，這些粒子在搜索空間中以一定的速度飛行，并根據粒子本身的及同伴的飛行經驗對自己的飛行速度進行動態調整，即每個粒子通過統計迭代過程中自身的最優值和群體的最優值來不斷修正自己的前進方向和速度大小，依據每個粒子對環境的適應度將個體逐步移到較優區域，并最終搜索、尋找到問題的最優解。該算法具有并行處理、魯棒性好等特點，能以較大概率找到問題的全局最優解，且計算效率比傳統隨機方法高。其最大優勢在于簡單易實現、收斂速度快，且有深刻的智能背景，被廣泛運用于PSS參數優化和其它電力系統問題[10]。粒子群算法的性能很大程度上取決于算法的控制參數，并直接影響最終解的質量。為此出現許多改進的粒子群算法，如帶壓縮因子的粒子群算法及權重改進的粒子群算法，目的均是為了提高算法尋優能力，避免粒子過早收斂到局部最優值。文獻[11]分別以機電暫態模型下使不良衰減特征根遠離復平面虛軸和最小機電阻尼比最大化為目標函數采用改進的PSO算法優化求解，以確定PSS參數的最佳位置。為進一步改善PSO算法的性能，文獻[12]以系統輸出按最小誤差跟蹤給定值的能力為目標函數，利用隨機聚焦粒子群算法優化PSS參數，以提高PSO算法的尋優性能。文獻[13]將混沌優化同PSO結合，用以提高PSO算法的尋優性能，在局部搜索過程中求得更精確的解。

針對基本PSO種群隨機初始化的盲目性，以及慣性權重系數對算法搜索性能的重要影響，在前述PSS參數優化研究的基礎上，提出一種基于自適應混沌粒子群優化ACPSO算法的PSS參數優化方法。該算法通過混沌初始化粒子，擇優選取初始種群，可加快進化過程；同時，利用自適應慣性權重平衡全局搜索能力和局部改良能力，保護了目標函數值優于平均目標值的微粒，對于目標函數值差的微粒，對應的慣性權重因子較大，使得該微粒朝更好的搜索空間靠攏。該算法簡單易行，計算效率高，收斂速度快，同時能夠克服基本PSO算法容易陷入局部最優解的不足，3機9節點算例結果表明運用該算法設計的PSS在不同運行方式下的有效性和魯棒性。

1 PSS參數優化問題的數學模型

1.1 電力系統模型

電力系統的數學模型可用如下非線性微分方程組和代數方程組來表示[14]：

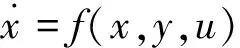
(1)

0=g(x，y)

(2)

式中：x為狀態變量向量；y為代數變量向量；u為控制變量向量。

當電力系統遭受小干擾時，根據李雅普洛夫線性化方法，將包含PSS的描述電力系統動態特性的微分-代數方程式在穩態運行點處線性化，消去變量后得到電力系統狀態方程：

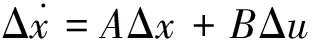
(3)

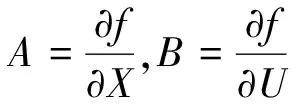
1.2PSS模型

本文PSS采用超前-滯后校正模型，其傳遞函數為[15]：

(4)

式中：Vsi為第i臺發電機PSS輸出信號；Twi為隔直環節時間常數；T1i、T2i、T3i、T4i為相位補償環節時間常數；發電機轉速偏差Δwi為PSS的輸入信號。

1.3PSS參數優化模型

通過裝有PSS的電力系統狀態矩陣的特征值可以判定系統在運行點的穩定狀況，對于表現為振蕩模式的共軛特征值λ=σ±jω，定義阻尼比[16]：

(5)

阻尼比反映了特征值在復平面上的位置，是度量系統動態性能的指標，將阻尼比作為優化目標函數能使電力系統滿足一定的動態響應指標。實際電力系統運行狀態經常發生變動，考察一種運行方式下的PSS參數優化配置可能在其它運行方式失效甚至惡化系統穩定性。考慮過多的運行方式又會造成優化計算的復雜性和最優參數組合尋優的困難。對此可在多種典型運行方式中選取一種基本運行方式，首先基于此方式進行PSS參數優化，然后在其它運行方式下進行校驗。若系統滿足穩定要求，說明設計的PSS對不同運行方式具有良好適應性，否則需要綜合考慮某些不滿足穩定要求的運行方式，重新進行參數優化配置或考慮其它控制策略。

基于上述思路和PSS參數的邊界限制，考慮Twi、T2i、T4i一般為給定值，PSS設計問題可以表述為如下帶約束的優化問題：

(6)

其中目標函數J定義為

J=min{ξi,j，i∈機電振蕩模態集合，

j=1，…，k}

式中：ξi,j為運行方式j下第i個機電振蕩模態的阻尼比；k代表考慮的運行方式數。

電力系統機電振蕩模態是通過參與因子(Participation factor)來進行篩選的。第k個狀態變量與第i模態的參與因子定義為

pki=ukivki

(7)

式中uki和vki分別表示第i個模態對應右、左特征向量中的第k個元素。參與因子度量了狀態變量與模態之間的相關程度，如果由參與因子組成的參與向量中模值最大的分量與發電機的轉速相關，則可以認為該模態為機電振蕩模態。

2 算法描述

2.1 基本粒子群優化算法

類似于其它群智能優化算法，粒子群優化算法利用粒子群進行搜索，每個粒子代表優化問題的一個解，具有位置和速度兩個變量。第i個微粒位置可以表示成n維向量，即Xi=(xi1，xi2，…，xin)，微粒的速度表示為Vi=(vi1，vi2，…，vin)。在迭代過程中，該粒子本身到目前為止經歷的最佳位置，稱為個體極值點pbest，整個群體到目前為止經歷的最佳位置，稱為全局極值點。粒子通過跟蹤兩個“極值”來更新自己，各個粒子按照gbest下述公式來更新自己的速度和位置變量：

(8)

(9)

式中i=1，2，…，m；m為微粒個數；j=1，2，…，n；n為自變量個數；t為當前迭代次數；w為慣性權重系數；c1，c2為正的學習因子；r1，r2是介于0到1之間的隨機數。

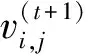
0.1≤k≤0.5

(10)

通過上述關于基本PSO算法的描述可以看出，該算法存在以下不足：

(1)初始化粒子種群帶有一定的盲目性，隨機初始化雖然可以基本保證初始解均勻分布，但可能有一部分粒子遠離最優解，影響進化過程的收斂。

(2)根據上述粒子速度和位置的更新公式可知，粒子的迭代過程是依據自身信息、個體極值以及全局極值信息來進行，當粒子本身信息和個體極值信息占優勢時，或者當pbest接近于gbest且w小于1時，粒子速度會越來越小，出現“惰性”，都使得算法容易陷入局部最優解。

2.2 自適應混沌粒子群優化算法

針對基本PSO算法的不足，本文采用自適應混沌粒子群優化算法對上述PSS參數優化問題進行求解，其主要思想是[17]：

1)利用混沌運動特有的遍歷性，對粒子群進行混沌初始化，從中擇優選出初始群體，以提高初始粒子種群的多樣性和粒子搜索的遍歷性。

2)考慮在PSO算法中，慣性權重系數w使粒子保持運動慣性，使其具有擴展搜索空間的趨勢，有助于新區域的搜索。w的取值對算法的性能具有重要影響，w取值大有助于全局搜索，但不易得到精確的解；取值小有助于進行局部搜索可得到更精確的解，但不易跳出局部極值點。結合混沌粒子群優化算法，慣性權重采用基于粒子個體適應值的自適應慣性權重

(11)

式中：wmax為慣性權重系數最大值；為wmin慣性權重系數最小值；favg為當前整個種群適應值的平均值；fmin為當前整個種群適應值的最小值；fi為粒子i當前的適應值。

3)按適應值大小從當前粒子群中擇優選取一部分粒子對其進行混沌優化，可使搜索過程具有避免陷入局部最優的能力。

基于上述思想，利用自適應混沌粒子群算法進行PSS參數優化的具體流程如下：

(1)PSS參數優化問題相關參數初始化。確定待優化的PSS參數維數n和相應參數的可行域(xmin，xmax)，設置初始粒子種群數m和學習因子c1，c2以及慣性權重系數w的上下限，最大迭代次數為M次。

(2)混沌初始化粒子群各粒子的位置和速度。隨機產生一個各分量均在0～1的n維向量Z1=(z11，z12，…，z1n)，以Z1為初始值，根據Logistic映射迭代公式：

z(t+1)=μz(t)(1-z(t))

(12)

式中：t為迭代次數；μ為控制參數，一般取4；迭代得到N個矢量Z1，Z2，…，ZN。將產生的矢量 各個分量利用類似載波的方式按式(13)引入到優化變量的取值范圍：

(13)

式中：i=1，2，…，N；j=1，2，…，n。計算各個矢量的適應度值，擇優選取最好的前m個作為粒子種群的初始位置并隨機產生m個初始速度。

(3)由式(10)計算各個粒子的慣性權重系數，根據式(7)～(9)更新各粒子的速度和位置。

(4)計算各粒子的適應值，若粒子的適應值優于原來的適應值，則更新個體極值點pbest及其適應值；若粒子的適應值優于原來的全局極值，則更新全局極值點gbest及其適應值。

(5)按適應值大小擇優選取前M(M=3)個粒子進行混沌優化。將各粒子Xp=(xp1，xp2，…，xpn)(p=1，2，…，M)的各個分量xpj(j=1，2，…，n)映射到Logistic方程的定義域上得：

(14)

(15)

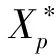
(7)判斷算法的終止條件是否滿足，若滿足轉向式(8)，否則轉向式(3)。

(8)輸出全局最優解gbest及其適應值。

3 算例仿真3.1PSS參數優化結果

本文以3機9節點系統為例，驗證ACPSO算法優化PSS參數的有效性。具體接線圖和網絡參數及發電機參見文獻[18]。發電機采用四階模型，并且均配置了自并勵靜止勵磁系統。勵磁系統參數統一為：KA=200，TR=0.01。待優化的PSS增益ki典型范圍為[0.01，50]，時間常數T1i、T3i典型范圍為[0.01，1.0]。時間常數Twi、T2i和T4i分別取固定值10，0.05和0.05。混沌初始化粒子種群大小為40，迭代次數取100，維數為6。通過模態分析確定G2和G3是安裝PSS的最佳位置。三種不同運行方式系統發電機出力和負載情況參見文獻[8]。

利用基本PSO和本文所述方法在基本運行方式(方式1)下得到的PSS參數如表1所示。采用系統特征值分析法，優化前后系統特征根和阻尼比如表2、3和4所示。從表2可以看出，系統在無PSS時，系統的兩個機電振蕩模式都呈現弱阻尼模式，表3和表4反映了在對應發電機處安裝PSS后，根據基本PSO和本文算法對PSS參數配置后系統機電振蕩模式阻尼比得到了有效提高。比較表3和表4結果，本文算法在搜索效率和精度方面較PSO性能更優，能在全局范圍內快速搜索更好的解。

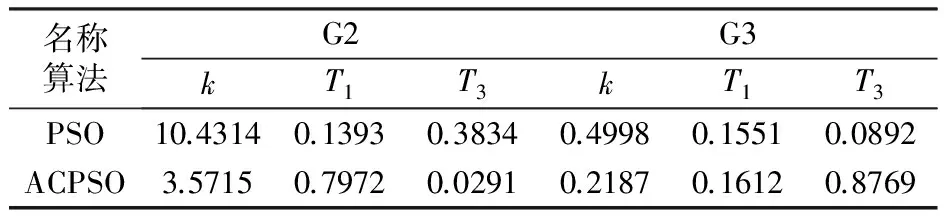
表1 利用PSO和ACPSO得到的PSS優化參數

表2 系統未安裝PSS時機電振蕩模態

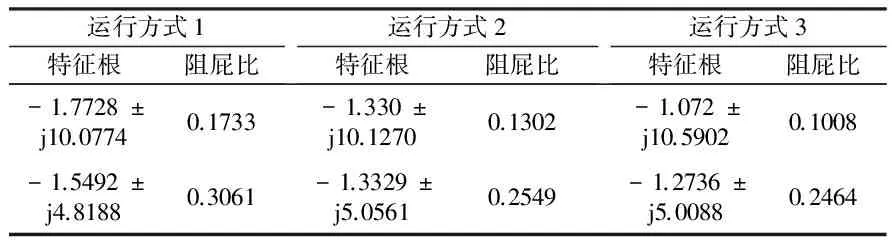
表3 PSO優化配置PSS后系統機電振蕩模態

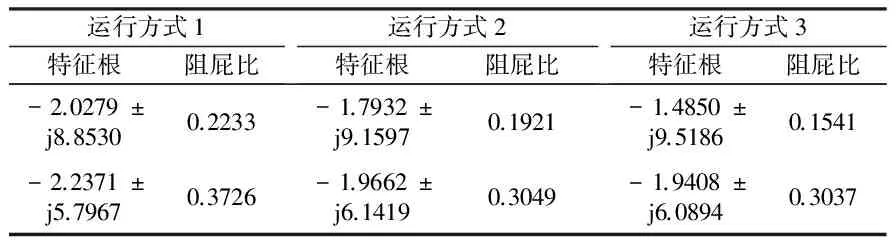
表4 ACPSO優化配置PSS后系統機電振蕩模態

圖1為PSO和ACPSO算法隨著迭代次數的增加目標函數的收斂變化情況。混沌初始化粒子群能使ACPSO算法以較好的初值進行優化搜索；盡管每代計算目標函數比PSO多出混沌優化所需次數(視混沌優化粒子數M而定)，從圖1中可以看出，與PSO算法相比ACPSO收斂速度和精度得到顯著提高，能在全局范圍內找到更好的解。

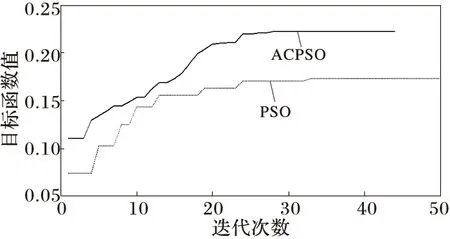
圖1 兩種優化算法下目標函數值變化曲線

3.2 動態仿真結果

在1.0 s時發電機G1出口發生三相短路，持續0.1 s情況下，對配置有該算法優化設計的PSS系統進行動態仿真。運行方式1下機組G1～G3相對轉子角振蕩曲線如圖2～4所示。

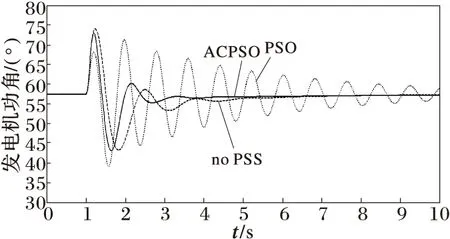
圖2 運行方式1下G1與G2之間的轉子角

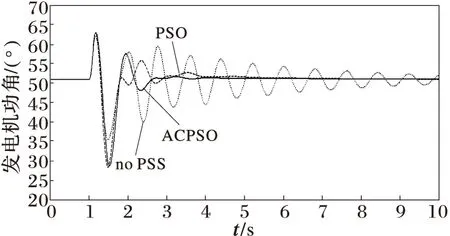
圖3 運行方式1下G1與G3之間的轉子角

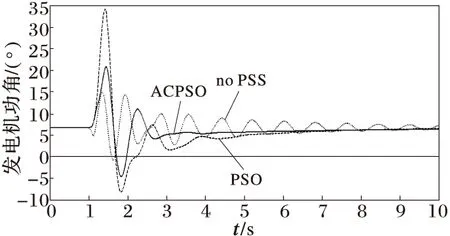
圖4 運行方式1下G2與G3之間的轉子角

可見，利用本文方法設計的PSS能改善系統動態性能和系統阻尼水平，方法性能優于基本PSO，能很快平息低頻振蕩，提高系統暫態穩定水平。

4 結語

對PSS參數設計是影響PSS性能的關鍵，本文利用ACPSO算法對PSS參數進行優化，以抑制電力系統受到外界干擾時可能引發的低頻振蕩。ACPSO算法利用自適權重平衡PSO算法的全局搜索和局部改良能力，結合混沌運動遍歷性特點克服了基本PSO算法容易過早陷入局部最優解，提高了搜索全局最優解的性能。本文以系統機電振蕩模式最小、阻尼比最大化為目標函數，考慮運行方式的影響，通過3機9節點的特征值分析和動態仿真結果表明，運用本文方法設計的PSS能夠在多種運行方式下有效地抑制系統低頻振蕩。

[1]Tse C T,Tso S K.Refinement of conventional PSS design in multimachine system by modal analysis[J].IEEE Transctions on Power System,1993,8(2):598-605.

[2]Kundur Prabhashankar,Klein Meir,Rogers Graham J,etal.Application of power system stabilizers for enhancement of overall system stability[J].IEEE Trans on Power Systems,1989,4(2):614-626.

[3]Abido M A.Novel approach to conventional power system stabilizer design using tabu search [J].International Journal of Electrical Power and Energy Systems,1999,21(6):443-454.

[4]Abido M A.Parameter optimization of multimachine power system stabilizers using genetic local search [J].International Journal of Electrical Power and Energy Systems,2001,23(8):785-794.

[5]Abido M A.An efficient heuristic optimization technique for robust power system stabilizer design[J].Electric Power Systems Research,2001,58(2):53-62.

[6]牛偉，房大中(Niu Wei,Fang Dazhong).基于GATS混合算法的PSS與SVC控制器參數設計(Coordination design of PSS and SVC damping controller using GATS hybrid algorithm)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA),2006,18(1):43-47,70.

[7]Abido M A,Abdel-Magid Y L.Optimal design of power stabilizers using evolutionary programming[J].IEEE Trans on Energy Conversion,2002,17(4):429-436.

[8]牛振勇,杜正春,方萬良,等(Niu Zhenyong,Du Zhengchun,Fang Wanliang,etal).基于進化策略的多機系統 PSS 參數優化(Parameter optimization of multi-machine power system stabilizers using evolutionary strategy)[J].中國電機工程學報(Proceedings of the CSEE),2004,24(2):22-27.

[9]Kennedy James,Eberhart Russell.Particle swarm optimization[C]// IEEE International Conference on Nerual Networks,Perth,Australia:1995.

[10]陳建華,李先允,鄧東華,等(Chen Jianhua,Li Xianyun,Deng Donghua,etal).粒子群優化算法在電力系統中的應用綜述(A review on application of particle swarm optimization in electric power systems)[J].繼電器(Relay),2007,35(23):77-84.

[11]Abido M A.Optimal design of power-system stabilizers using particle swarm optimization[J].IEEE Trans on Energy Conversion,2002,17(3):406-413.

[12]吳峰,魯曉帆,陳維榮,等(Wu Feng,Lu Xiaofan,Chen Weirong,etal).電力系統穩定器參數優化的研究(Research of parameter optimization of power system stabilizer)[J].電力系統保護與控制(Power System Protection and Control),2010,38(5):29-33,44.

[13]劉自發,葛少云,余貽鑫(Liu Zifa,Ge Shaoyun,Yu Yixin).基于混沌粒子群優化方法的電力系統無功最優潮流(Optimal reactive power dispatch using chaotic particle swarm optimization algorithm)[J].電力系統自動化(Automation of Electric Power Systems),2005,29(7):53-57.

[14]Kundur P.Power System Stability and Control [M].New York:McGraw-Hill,1994.

[15]劉取.電力系統穩定性機發電機勵磁控制[M].北京：中國電力出版社,2007.

[16]倪以信,陳壽孫,張寶霖.動態電力系統的理論和分析[M].北京:清華大學出版社,2002.

[17]周孝法,陳陳,楊帆,等(Zhou Xiaofa,Chen Chen,Yang Fan,etal).基于自適應混沌粒子群優化算法的多饋入直流輸電系統優化協調直流調制(Optimal coordinated HVDC modulation based on adaptive chaos particle swarm optimization algorithm in multi-infeed HVDC transmission system)[J].電工技術學報(Transactions of China Electrotechnical Society),2009,24(4)：193-201.

[18]Anderson P M,Fouad A A.Power System Control and Stability[M].Iowa:The Iowa State University Press,1977.

陳 剛(1964-)，男，副研究員，研究方向為電力系統運行與控制、微機在電力系統中的應用、電力MIS系統、人工智能及負荷預測等。Email:cq@cqu.edu.cn

簡華陽(1985-)，男，碩士研究生，研究方向為電力系統運行與控制。Email:jhycarry2004@126.com

龔 嘯(1986-)，男，碩士研究生，研究方向為電力系統運行與控制。Email:gongxiao869@163.com

DesignofPowerSystemStabilizersUsingAdaptiveChaosParticleSwarmOptimizationAlgorithm

CHEN Gang，JIAN Hua-yang，GONG Xiao

(State Key Laboratory of Power Transmission Equipment amp; System Security and New Technology,College of Electric Engineering,Chongqing University,Chongqing 400044,China)

In order to damp the low frequency oscillation in power system,an improved particle swarm optimization called adaptive chaos particle swarm optimization(ACPSO)is applied to optimize the parameters of the multi-machine power system stabilizers(PSS).According to the proposed ACPSO algorithm,the capability of global search and convergence rate are improved by using the chaos motion to initialize the swarm,and each particle adjust its inertia weight factor adaptively in accordance with its fitness value in the process of the iterative calculation.The maximized minimum damping among all electromechanical oscillation modes is taken as the objective function,and then the optimization of parameters of the PSS is converted to the nonlinear optimization problem with the inequality constraints.The proposed method is tested on 3 machines and 9 buses system,and the results of both the eigenvalue and nonlinear simulation show that the PSS optimized by proposed ACPSO algorithm can effectively damp the low frequency oscillation caused by external disturbance.

multi-machine power system；power system stabilizer(PSS)；adaptive chaos particle swarm optimization algorithm(ACPSO)；low frequency oscillation；power system stability

TM715

A

1003-8930(2012)04-0082-06

2011-01-04；

2011-03-09