計及低碳效益的分布式發電優化配置

鄧 晶，周任軍，鄭 思，任俞霖

（長沙理工大學，智能電網運行與控制湖南省重點實驗室，長沙410114）

分布式電源（包括儲能）大量接入電網，是順應環境保護、節能減排和可持續性發展的重要趨勢。研究表明DG不同的安裝位置和容量，將會影響到系統短路電流的大小、配電網的電壓分布、系統網損、繼電保護等［1～3］。

分布式電源選址和定容的問題屬于多變量優化問題，國內外學者從不同角度對DG優化配置問題進行了研究，取得了豐富的成果。文獻［4］建立了鏈式配電網絡、恒功率靜態負荷模型和分布式電源的功率模型，提出一種圖解與遺傳算法相結合的計算方法。文獻［5］研究了多負荷水平下計及節能調度的配電網分布式電源（DG）優化配置問題，建立了2層規劃數學模型，使DG并網運行價值最大化。文獻［6］對分布式發電的可行接入位置以及注入容量限制進行了理論探討。文獻［7］通過計算微增率確定分布式發電的安裝位置，在確定容量時，充分考慮環境因素，使得結果有利于環境保護。文獻［8］采用Tabu搜索算法求解分布式優化配置問題。文獻［9］以最大化有功輸出為目標函數，將線路的熱穩定極限加入約束中，利用線性規劃求解規劃模型。文獻［10］提出的規劃模型以供電公司的總成本最小為優化目標。

但是國內外文獻中將低碳效益和分布式發電優化配置相結合的研究尚不多見。通常人們認為，開展分布式發電優化配置研究的主要目標是降低網損，提高經濟效益，減少SO2等污染氣體的排放，對低碳效益卻缺乏足夠重視，而現實情況是：作為CO2排放的主體，有效控制并減少碳排放成為電力行業所面臨的突出問題，而電源規劃則將在其中發揮著至關重要的作用。所以將低碳效益納入優化配置模型中具有實際意義。

基于以上原因，本文針對電力系統各個環節進行低碳分析，推導出發電側低碳費用的計算公式，首次將低碳效益作為評估配電網效益的重要指標加入分布式發電多目標優化配置模型，改變了傳統的分布式發電優化配置模式，使分布式發電的節能減排優勢最大化。

1 電力系統低碳分析

在整個電力系統中，低碳概念不僅在其能源側、發電側，而是在輸配電側、用戶側等各個環節均有影響。針對每個環節，分析和總結出各自實現低碳電力的關鍵技術和措施，如表1所示。

表1 電力系統低碳環節分析及技術措施Tab.1 Power system low－carbon analysis and technical measures

發電側作為電力生產鏈的源頭，在實現低碳電力中扮演非常重要的角色，中國電力生產主要所利用的一次能源以煤炭為主，生產單位電能的CO2排放強度約為0.82kg／（kW·h）［11］，所以現階段實現發電側低碳化顯得更加緊迫，而風電、光伏等近零碳排放發電的并網正是實現發電側低碳化的最佳途徑。

2 分布式發電優化配置指標

2.1 低碳費用指標

相對于傳統火力發電機，DG排放很少量的CO2，所以DG的接入能夠有效降低低碳費用，提高低碳效益。

1）低碳費用成本

低碳費用成本由低碳投入成本和低碳損失成本兩部分組成，即

其中：cc為低碳費用成本；cd為低碳投入成本；cf為低碳損失成本。

低碳投入成本cd是指發電商為減輕碳污染，從事節能減排活動而支付的費用，這部分成本可根據設備技術初投資、相關運行活動費用估算得出。

低碳損失成本cf指的是發電機因排放二氧化碳而支付的費用成本，即發電商向政府部門交納的碳排放費或者罰款的費用成本，這部分成本是根據國家制定的碳排放收費標準和二氧化碳的排放量計算得出：

式中：Eco2為發電機單位有功出力產生的CO2的排放量；λco2為CO2排放懲罰價格。

2）低碳費用指標

低碳費用指標ΔE可表示為

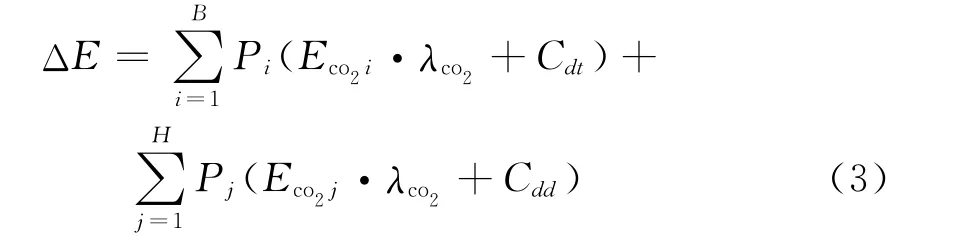
式中：B、H分別為系統中傳統發電機臺數和DG臺數；Pi、Pj分別為傳統發電機和DG的有功出力；Eco2i、Eco2j分別為傳統發電機和DG單位有功出力產生的CO2排放量；λco2為CO2排放懲罰價格；Cdt、Cdd分別為傳統發電機和DG的低碳投入成本。

2.2 電壓安全指標

在分布式電源接入配電網之后，配電系統從放射狀無源網絡變為有源網絡，潮流的大小和方向都將發生巨大改變，從而使配電網中某些位置的電壓也發生變化。電壓安全指標的建立能夠評估DG的位置和注入功率對配電網全局電壓的影響，而用戶要求節點電壓在保證合格的基礎上盡量減少與標準值1.0（標幺值）的偏差，所以定義電壓安全指標為各節點的電壓偏移總和［12］：

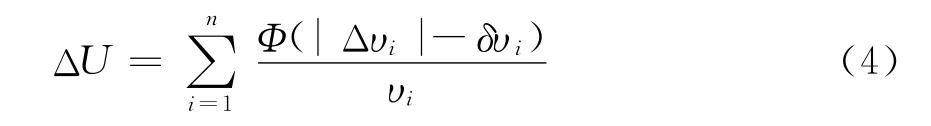
式中：n為配電網的節點數；υi為節點i的電壓；Δυi為節點i的電壓偏差量。標幺化以后，Δυi＝1－υ；δυI為節點i可忽略的最大電壓偏差量；設x＝｜Δυ｜－δυi，則函數Φ（x）可以表示為

本文取δυi為－1% ～＋1%，當電壓偏差在這個范圍內時認為電壓偏差忽略不計。

2.3 有功網損指標

分布式電源接入配電網改變了系統潮流分布，一般會減小支路潮流流動，從而有利于減小網損，但是當DG注入功率過高時，支路潮流流動反而可能增大，所以網絡損耗不僅與負荷大小有關，同時還與分布式電源的安裝位置以及分配到各節點的功率值有關。采用配電網支路的有功網損的總和作為指標：

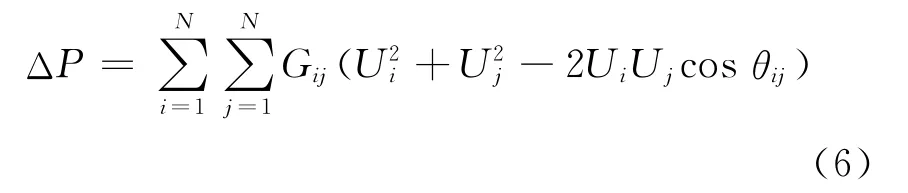
式中：N為系統節點數；Gij為線路ij的電導；Ui／Uj分別為節點i和j的節點電壓；θij為節點i與節點j之間的相角差。

3 分布式發電配置多目標優化模型

3.1 目標函數

由上可知，分布式電源接入配電網后，對低碳費用、電壓安全、有功網損都會帶來影響，以此三項指標作為分布式電源優化配置問題的多目標，其目標函數：

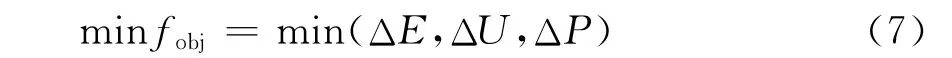
其中，ΔE，ΔU，ΔP分別如式（3）、（4）、（6）描述。

3.2 約束條件

等式約束為潮流方程：

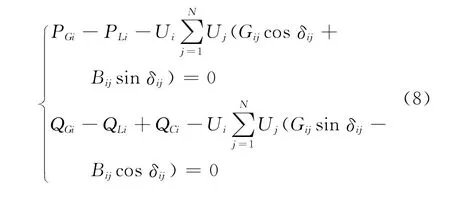
不等式約束為

式中：PGi、QGi分別為發電機有功、無功出力；PLi、QLi分別為發電機有功、無功負荷；QCi為無功補償容量；Ui為節點電壓大小；Gij、Bij為系統導納；δij為節點電壓相角差；Pdi、Qdi分別為DG的有功、無功出力；j∈i表示與節點 相連的節點；變量添加下標min、max分別表示該變量的下限和上限。

3.3 優化模型轉換

由于3個優化子目標具有不同的量綱，為協調不同目標之間的關系，本文在多目標優化模型中引入滿意度值μ。μ是與各個目標函數值相關的復合函數，也稱為隸屬度函數。它反映了多目標優化結果與各個單目標優化結果之間的“距離”。滿意度值越大，相應的解與單目標優化解越接近。于是原來的多目標優化問題就轉化成以隸屬度函數值最大為目標的單目標優化問題，引入降半直線型函數來表示各子目標的模糊隸屬度函數：

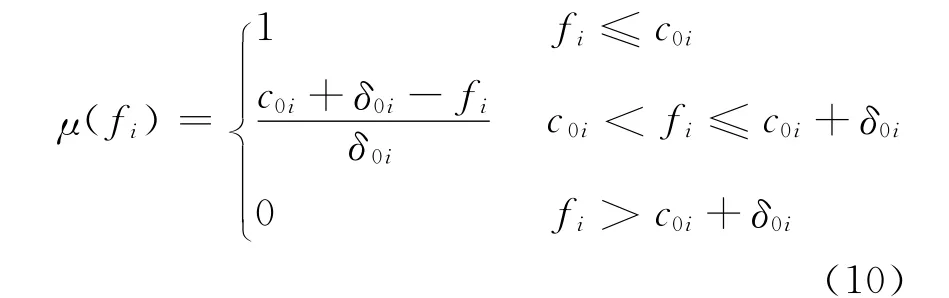
式中：i＝1，2，3；μ（fi）對應低碳效益、電壓安全和有功網損3個優化子目標的隸屬度；c0i為對3個子目標單獨優化得到的最佳目標值；c0i＋δ0i表示目標函數優化中最高可接受的上限值。

經過上述模糊化處理，原多目標規劃問題就轉化為單目標規劃問題：

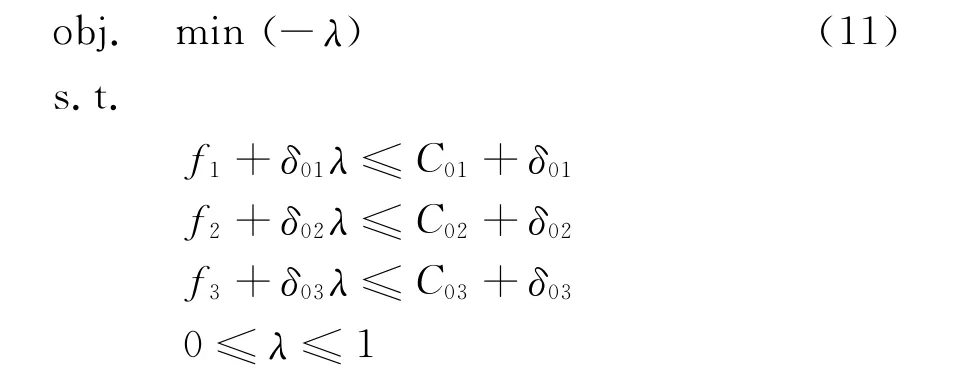
式 中：λ為 總 體 滿 意 度，λ＝ min｛μ（f1），μ（f2），μ（f3）｝。

約束還有式（8）、式（9）。

4 模擬植物生長算法求解DG規劃

模擬植物生長算法是將優化問題的可行域作為植物的生長環境，將全局最優解當作光源，模擬真實植物生長的向光性機理，建立枝葉在不同光線強度環境下向光源快速生長的動力機制［13］。文獻［14］采用以植物向光性理論為基礎的概率生長模型對這一過程進行了模擬。假設樹干的長度為M，樹從樹根所在的點S0開始生長，在經歷若干次生長后，上面有k個比樹根好的初始生長點SMk，所對應的形態素濃度為PMk，按下式計算樹上各生長點的形態素濃度值：

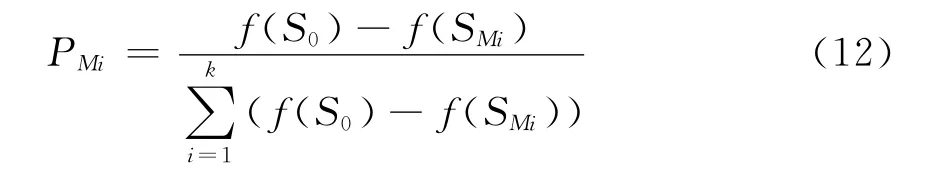
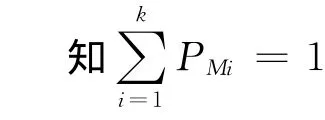
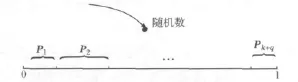
圖1 形態素濃度構成的狀態空間Fig.1 Morphactin concentration state space

利用PGSA求解DG優化配置的流程如圖2所示。

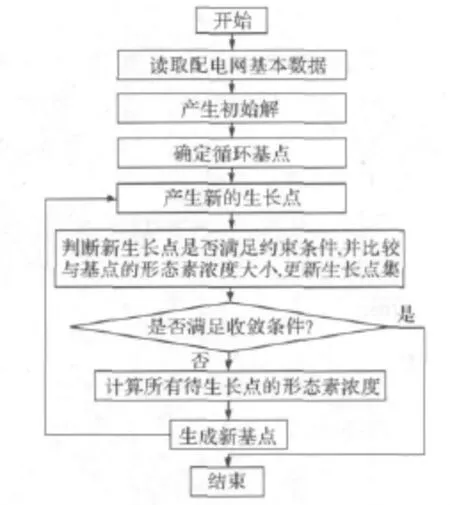
圖2 PGSA求解DG規劃流程Fig.2 Flow chart of planning of DG based on PGSA

DG優化配置涉及到DG待選節點和安裝容量兩個決策變量。待選節點可以描述成整數序列形式，｛m1、m2、m3、…，mNDG｝，則節點mi處 DG 的安裝容量為mipr，當mi為0時表示該節點不安裝DG。規劃程序首先單獨以式（3）、式（4）和式（6）這3個優化子目標為適應度函數，分別求出c01、c02和c03；然后再以式（11）為目標進行優化，求出總體滿意度最好的DG規劃方案。

5 算例分析

以IEEE30節點系統為例，根據本文提出的方法計算分布式電源最佳位置和最佳容量。

IEEE30節點系統中包括6臺發電機（1、2、5、8、11、13號節點上接有常規機組，節點1為平衡節點）、4臺變壓器、4個無功補償裝置，有功負荷為162MW，無功負荷為94Mvar。算例中所采用的DG的額定容量為100kW，各待選節點允許安裝的最大容量為1MW，DG規劃總容量不超過1MW。假設只在三個節點接入分布式電源，選取節點7、9、10、14、15、17、22、23、24、29、30 作 為 并 網 備選點。

表2是本文根據傳統發電廠的機組特性和相關環境政策設定的IEEE 30節點系統發電機低碳費用的計算參數，并假設DG釋放的二氧化碳量很少，可以忽略不計。

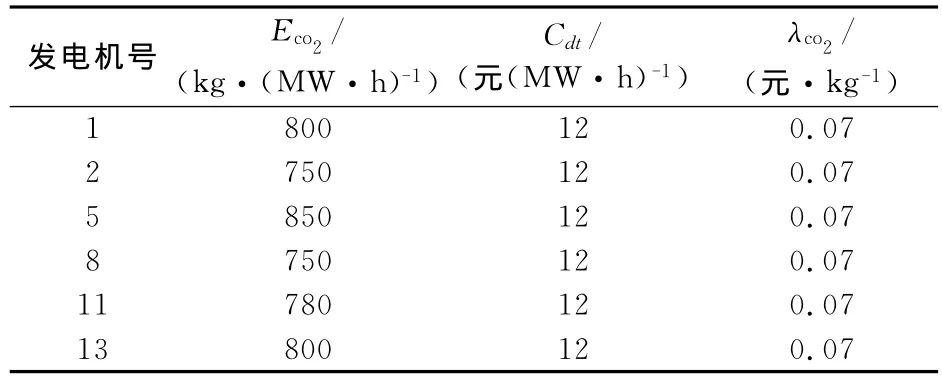
表2 系統發電機低碳費用的計算參數Tab.2 Calculation parameters of low－carbon expense in generator

分別計算出在未安裝DG時和安裝DG后系統的低碳費用、電壓安全和系統網損，計算結果如表3所示。

表3 系統優化結果Tab.3 System optimization result

求解得出DG的最優配置為：節點30安裝5臺，節點9安裝3臺，節點15安裝2臺；3個優化指標的值分別為 ΔE＝64元、ΔU＝0.0104、ΔP＝3.7560MW。算例計算結果（見表3）表明，安裝DG后系統的低碳費用、比安裝DG前都有所降低，節點電壓安全指標由0.0127下降到0.0104，有功網損由4.9562MW 降低到3.7560MW。由此可見，采用本文方法確定DG的地址和出力，可有效減少碳排放，改善系統的運行條件，提高系統電壓的運行水平，減少有功網損。

表4是針對各個單目標進行規劃的結果，其中方案1、方案2和方案3分別對應低碳效益、電壓安全和有功網損三個子目標的DG優化配置，求得的f1，f2和f3分別為62元／（MW·h），0.0000和3.204MW。從表3可知：方案1只強調了低碳費用的減少，而在降低網損和改善系統電壓安全性方面有所欠缺；方案2強調改善系統電壓安全性，但是同樣在低碳費用上付出了更高的代價；方案3強調了網損的優化，但是在其他兩方面都受到相應的損失。

表4 單目標優化結果Tab.4 Single objective optimization result

比較表3和表4數據可知：相對于單目標優化模型，多目標優化模型確定的DG配置能在各目標之間進行協調權衡，使所有目標函數盡可能達到最優，綜合效益更高，更能滿足實際需求。

表5比較了PGSA和遺傳算法GA（genetic algorithm）對算例的仿真情況。兩種算法得到的優化結果完全一致，計算時間略有不同。與遺傳算法相比，PGSA不需要設置懲罰系數、交叉率、變異率等影響算法計算速度和收斂性的參數，算法的穩定性高，計算時間短。

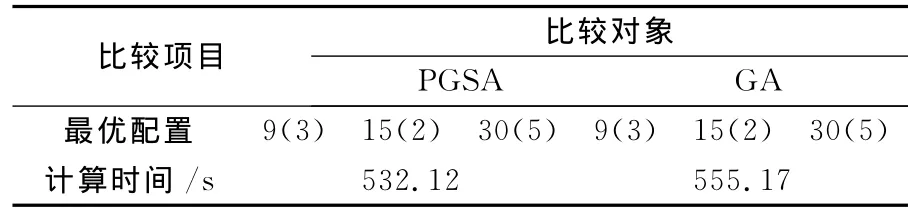
表5 植物生長模擬算法與遺傳算法的比較Tab.5 Comparison of PGSA and GA

6 結語

在分析和總結低碳電力發展的基礎上，提出發電側低碳費用的計算公式，以低碳費用、電壓安全、有功網損三個指標評估含分布式發電的配電網效益，建立分布式發電配置的多目標優化模型，采用最大滿意度法轉化多目標優化問題為單目標，并用模擬植物生長算法對上述模型進行求解。算例分析表明：將低碳效益納入優化模型中，能夠更加全面地評估分布式發電的優勢，改變了傳統分布式發電優化配置中只考慮經濟效益的單一模式，有效減少二氧化碳的排放，提高系統電壓的運行水平，降低系統有功網損。

［1］ 王守相，王慧，蔡聲霞（Wang Shouxiang，Wang Hui，Cai Shengxia）.分布式發電優化配置研究綜述（A review of optimization allocation of distributed generations embedded in power grid）［J］.電力系統自動化（Automation of Electric Power Systems），2009，33（18）：110－115.

［2］ 張勇（Zhang Yong）.分布式發電對電網繼電保護的影響綜述（Review of impact of distributed generation on distribution system protection）［J］.電力系統及其自動化學報（Proceedings of the CSU－EPSA），2010，22（2）：145－151.

［3］ Naveen Jain，Singh S N，文福拴（Wen Fushuan）.分布式發電當前趨勢與將來挑戰（Distributed generation recent trends and future challenges）［J］.電力科學與技術學報（Journal of Electric Power Science and Technology），2008，23（4）：53－61.

［4］ 李鵬，廉超，李波濤（Li Peng，Lian Chao，Li Botao）.分布式電源并網優化配置的圖解方法（A graph－based optimal solution for siting and sizing of grid－connected distributed generation）［J］.中國電機工程學報（Proceedings of the CSEE），2009，29（4）：91－96.

［5］ 唐勇俊，劉東，阮前途，等（Tang Yongjun，Liu Dong，Ruan Qiantu，etal）.計及節能調度的分布式電源優化配置及其并行計算（Optimal allocation of distributed generation and its parallel computation considering energy－saving dispatching）［J］.電力系統自動化（Automation of Electric Power Systems），2008，32（7）：92－97.

［6］ 王志群，朱 守真，周雙 喜，等 （Wang Zhiqun，Zhu Shouzhen，Zhou Shuangxi，etal）.分布式發電接入位置和注入容量限制的研究（Study on location and penetration of distributed generations）［J］.電力系統及其自動化學報（Proceedings of the CSU－EPSA），2005，17（1）：53－58.

［7］ 鄭漳華，艾芊，顧承紅，等 （Zheng Zhanghua，Ai Qian，Gu Chenghong，et al）.考慮環境因素的分布式發電多目標優化配置（Multi－objective allocation of distributed generation considering environmental factor）［J］.中國電機工程學報（Proceedings of the CSEE），2009，29（13）：23－28.

［8］ Gandomkar M，Vakilian M，Ehsan M.A genetic based Tabu search algorithm for optimal DG allocation in distribution networks ［J］.Electric Power Components and Systems，2005，33（12）：1351－1362.

［9］ Keane A，O＇Malley M.Optimal allocation of embedded generation on distribution networks［J］.IEEE Trans on Power Systems，2005，20（3）：1640－1646.

［10］ El－Khattam W，Bhattacharya K，Hegazy Y，et al.Optimal investment planning for distributed generation in a competitive electricity market［J］.IEEE Trans on Power Systems，2004，19（3）：1674－1684.

［11］ 陳 啟 鑫，康 重 慶，夏 清，等 （Chen Qixin，Kang Chongqing，Xia Qing，et al）.電力行業低碳化的關鍵要素分析及其對電源規劃的影響（Key low－carbon factors in the evolution of power decarbonisation and their impacts on generation expansion planning）［J］.電力系統自動化（Automation of Electric Power Systems），2009，33（15）：18－23.

［12］ 王新剛，艾芊，徐偉華，等（Wang Xingang，Ai Qian，Xu Weihua，et al）.含分布式發電的微電網能量管理多目標優化（Multi－objective optimal energy management of microgrid with distributed generation）［J］.電力系統保護與控制（Power System Protection and Control），2009，37（20）：79－83.

［13］ 李彤，王春峰，王文波，等（Li Tong，Wang Chunfeng，Wang Wenbo，et al）.求解整數規劃的一種仿生類全局優化算法——模擬植物生長算法（A global optimization bionics algorithm for solving integer programming－Plant growth simulation algorithm ）［J］.系統工程理論與實踐（Systems Engineering－Theory＆ Practice），2005，25（1）：76－85.

［14］ 楊麗徙，王鍇，程杰（Yang Lixi，Wang Kai，Cheng Jie）.應用改進模擬植物生長算法求解無功優化問題（Application of modified plant growth simulation algorithm in solution of reactive power optimization problem ）［J］.高電壓技術（High Voltage Engineering），2009，35（3）：694－698.