薄壁空心高墩施工階段順風向風振響應分析
王振興 高良艷 姬志洋
(河南省第五建筑安裝工程集團有限公司,河南鄭州 450007)
0 引言
風荷載是作用在結構上的重要動力荷載之一,對于高層建筑結構、高聳結構(高墩、電視塔、煙囪等),有時甚至起決定性作用。
研究風荷載作用下薄壁高墩風振響應分析,除了現場測試、風洞實驗方法之外,在理論上主要有兩種方法,一種是頻域法(Frequency domain),它按隨機振動理論,建立了輸入風載荷譜的特性與輸出結構響應之間的直接關系;另一種是時域法(Time domain),它是基于將隨機的風荷載模擬成時間函數,然后直接求解運動微分方程。本文主要通過頻域法研究薄壁高墩施工階段在風載荷作用下的風致振動規律。
1 高墩脈動風基本參數
1.1 工程簡介
西張村大橋位于省道S318線石原至三門峽西站段改建工程東段。由于橋區地貌單元為中低山河谷地,水文地質單元為中低山河谷型孔隙、孔隙潛水區,該橋跨越的南北地溝溝深坡陡,其中①~⑥橋墩采用矩形空心薄壁墩,凈高分別為57m,68.5m,76m,83m,63m以及43m,其中④墩凈高83m,為河南省公路建設歷史上的第一高墩,建設技術含量高,施工建造技術復雜。
1.2 脈動風荷載基本參數
根據三門峽西張村大橋的使用功能,結構重要性系數為1.1,設計使用年限為100年,由GTJ/T D60-01-2004公路橋梁抗風設計規范附表A可得,三門峽地區采用重現期為100年,基本風速為27.7m/s,基本風壓為0.45kN/m2,表1列出了脈動風速需要的一些基本數據。
根據隨機振動理論,在利用頻域法分析薄壁高墩順風向風振響應之前,首先要求出該高度處的平均風速和平均風壓。同時,根據薄壁空心高墩施工階段的結構形式,可以把其計算模型簡化為一維多自由度集中質量懸臂體系,薄壁空心墩具有高柔性特性,故將其簡化為豎向10個集中質量的計算模型。圖1顯示了10個集中質量的計算模型的簡圖。
表2列出了薄壁空心墩集中質量處的平均風速和平均風壓。

表1 薄壁空心墩脈動風速基本數據

表2 集中質量處的基本風速和基本風壓
2 頻域內高墩順風向風振響應分析
2.1 頻域法基本理論
頻域內計算風振響應的途徑,Davenport是這一方法的開創者,他引入了氣動導納和機械導納的概念,利用氣動導納把風速譜轉換到風壓譜,利用機械導納把風壓譜轉換到響應譜,建立起聯系風速資料、結構動力特性和結構響應的橋梁,為結構風效應的研究開辟了道路。
頻域內計算響應的基本思想是通過結構的響應傳遞函數計算響應譜密度。第一步通過位移傳函數,即位移導納來完成;第二步通過數值積和模態疊加來完成。因此該方法也稱為功率積分法。

2.2 順風向風振響應頻域分析
施工階段的薄壁空心高墩可以視為一維的豎向高聳懸臂結構,豎向把高墩簡化為10個質量點的多自由度體系。高墩底部為7m×5.128m的矩形,頂部為7m×3.50m的矩形,寬邊錐度為0.01,墩高83m。高墩的迎風向為長邊,沿高度方向沒有變化,高墩底部寬度B0=7m,墩頂寬度BH=7m。
1)薄壁高墩靜動力風荷載計算。
墩高H=83m,并根據GTJ/T D60-01-2004公路橋梁抗風設計規范判定高墩屬于D類地面粗糙度類別,脈動影響系數n=0.89。
由該高墩的底部寬度B0和頂部寬度BH分別為7m,其比值B0/BH=1.0,則得qv=1.00,并且由表1可以查出該地區的基本風壓為0.45kN/m2,由風振系數為
下面把Pi的計算過程列于表3中。

表3 薄壁高墩各點靜動力風荷載
由計算結果可知,薄壁空心高墩順風向墩底設計風荷載彎矩M0為:M0=15931.8kN·m。
如果按照GTJ/T D60-01-2004公路橋梁抗風設計規范規定:橋墩、橋塔、吊桿上的風荷載、橫橋向風作用下的斜拉橋斜拉索和懸索橋主攬上的靜風荷載可按下式計算:

其中,e為空氣密度,ρ=0.0012t/m3;Vg為靜陣風風速,可以按照距離地面0.65倍的墩高處的風速值確定,Vg=GVVZ=1.56×45.9=71.6m/s,GV為靜陣風系數,橋墩自立階段按照水平加載長度小于20m選取,故GV=1.65,VZ為基準高度Z處的風速,VZ=V10× (Z/10)0.3=27.7 × (54/10)0.3=45.9m/s;CH為橋墩阻力系數,根據橋墩的截面形狀和高寬比,可以求得其值為2.0;An為橋墩順風向投影面積,An=83×7=581m2。
通過風振系數法計算的墩底彎矩與橋梁靜陣風法計算的墩底彎矩比較發現,兩者相差72.9kN·m,誤差為0.46%,兩種方法計算結果非常接近,說明按照風振系數法和橋梁靜陣風法計算高墩順風向風振響應都能滿足要求,并且誤差很小。
2)薄壁高墩墩頂位移計算。
首先采用風振系數法計算墩頂位移,把風振系數法靜動力風荷載計算結果,各質量點靜動力風荷載施加在各質量點處,按照結構力學知識計算出各質量點順風向最大靜位移。其次用橋梁靜陣風法計算墩頂位移,把橋梁靜陣風荷載施加在0.65倍墩高處,計算各質量點順風向最大靜位移。兩種方法的計算結果見表4。對比兩種方法的墩身位移計算結果可知,雖然橋梁靜陣風法結果略大,但二者計算結果非常接近,證明兩種計算方法都適用順風向高墩風振響應的計算。
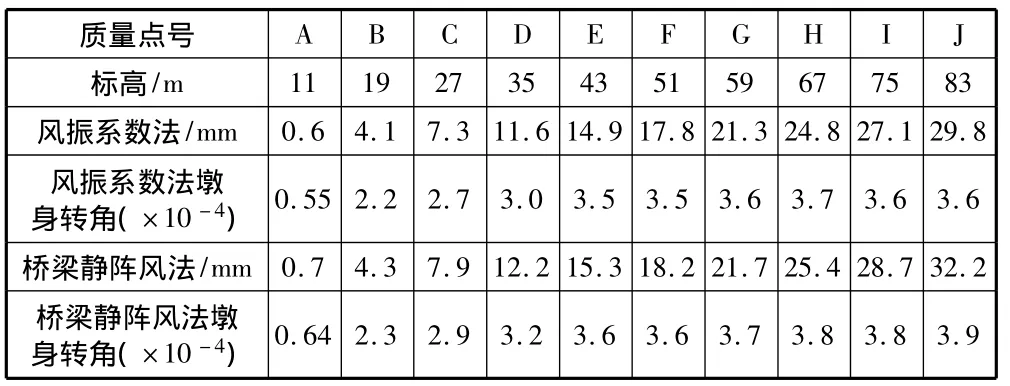
表4 薄壁高墩位移計算結果
3 結語
本文利用風振系數法和橋梁靜陣風法計算了薄壁空心高墩施工階段順風向風振響應,得出如下結論:
1)兩種計算方法難易程度相當;
2)兩種方法計算結果對比表明,誤差很小,都可以適用于此類結構相同荷載條件下的計算;
3)雖然頻域內的方法適用于此類結構計算,但要想精確分析脈動風對結構產生的響應,還需采用時域方法。
[1]GB50009-2001,建筑結構荷載規范[S].
[2]GTJ/T D60-01-2004,公路橋梁抗風設計規范[S].
[3]張相庭.工程結構風荷載理論和抗風設計手冊[M].上海:同濟大學出版社,1990.
[4]黃本才.結構抗風分析原理及應用[M].上海:同濟大學出版社,2001.

