一道課本習題的解法探究及應用

●

(深圳市高級中學 廣東深圳 518040)

一道課本習題的解法探究及應用

●黃元華

(深圳市高級中學 廣東深圳 518040)

本文研究一道關于直線與圓位置關系的課本習題(蘇教版高中數學必修2第118頁第26題).同類題目在各種高中數學考試試題與教輔資料中頻繁出現，但不少高中階段的學生對此類題目望而生畏，故有必要對其解法加以深入研究.該題的解法較多，本文就不一一呈現，只提供2種比較特殊的解法，并拓展應用到解決一般的圓錐曲線問題中.

1 原題呈現

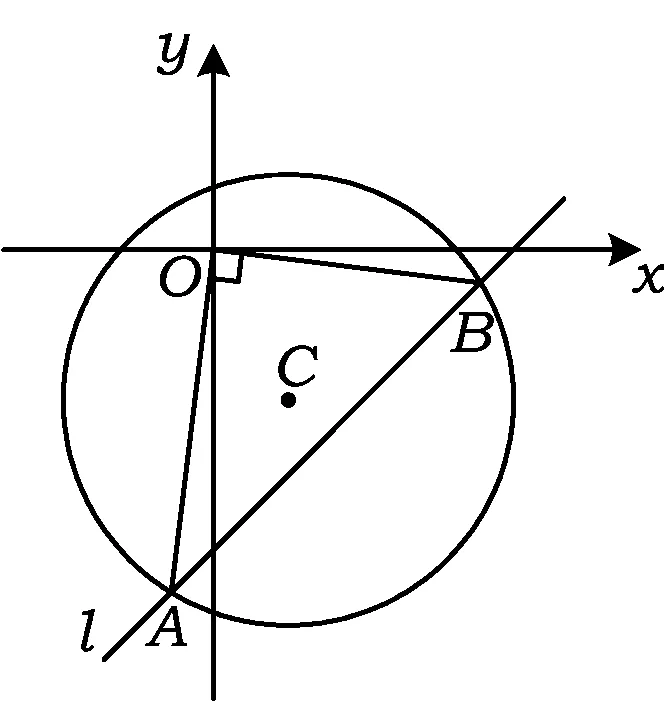
圖1

題目如圖1所示，已知圓C:x2+y2-2x+4y-4=0，是否存在斜率為1的直線l,使以l被圓C截得的弦AB為直徑的圓過原點?若存在,求出直線l的方程；若不存在,說明理由.

2 解法探究

解法1設A(x1,y1),B(x2,y2).假設該圓過原點O，則OA⊥OB，從而

kOA·kOB=-1，

即

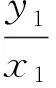
設所求直線l的方程為y=x+m，即

圓C方程為x2+y2-2x+4y-4=0，即

將式(1)代入式(2)，得

(m2+2m-4)x2+(m2+4m-4)y2+(8-6m)xy=0，

變形為

由韋達定理得

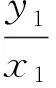
解得

m=1或m=-4，

故所求直線方程為y=x+1或y=x-4.

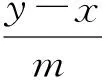
解法2設A(x1,y1),B(x2,y2).聯立直線l與圓C的方程,分別消去y,x,得

式(3)+式(4),得

2x2+2y2+2(m+1)x+2(1-m)y+2m2+6m-8=0.

因為該圓過原點O(0，0),所以

m2+3m-4=0，

解得

m=1或m=-4,

故所求直線方程為y=x+1或y=x-4.

評注此法構思巧妙，它提供了一種求以直線和圓錐曲線的相交弦為直徑的圓的方程的方法,即將直線方程與曲線方程聯立,分別消去x，y,得到關于y，x的2個一元二次方程,然后2式迭加,即得所求圓的方程.其原理何在？簡述如下：

若圓的一直徑的2個端點分別為A(x1,y1)，B(x2,y2),則圓的方程為

(x-x1)(x-x2)+(y-y1)(y-y2)=0,

變形即為

x2-(x1+x2)x+x1x2+y2-(y1+y2)y+y1y2=0.

該式可看作是

x2-(x1+x2)x+x1x2=0

與

y2-(y1+y2)y+y1y2=0

迭加而成，且一次項和常數項明顯呈現出韋達定理的特征．據此可知，對于某些直線與圓錐曲線相交的問題，可將直線方程代入曲線方程，分別得出關于x及y的一元二次方程，然后2式迭加即得以直線與曲線相交弦為直徑的圓的方程．

3 拓展應用

下面用解法1和解法2各解決2個相關的圓錐曲線問題.

圖2

例1如圖2所示，已知直線y=x+b與拋物線x2=2y交于點A,B,且OA⊥OB(O為坐標原點),求b的值.

解設A(x1,y1),B(x2,y2).直線l的方程y=x+b,即

拋物線方程為x2=2y·1,

(6)

將式(5)代入式(6),得

整理得

2y2-2xy-bx2=0,

即

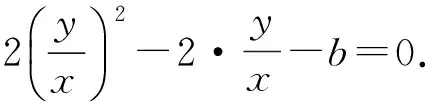
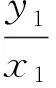
從而

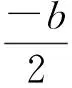
解得

b=2．

例2如圖3所示，已知橢圓C的中心在坐標原點,焦點在x軸上,橢圓C上的點到焦點距離的最大值為3,最小值為1.

圖3

(1)求橢圓C的標準方程.

(2)若直線l：y=kx+m與橢圓C相交于點A,B(A,B不是左、右頂點),且以AB為直徑的圓過橢圓C的右頂點.求證:直線l過定點,并求出該定點的坐標.

(2007年山東省數學高考理科試題)

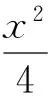
(2)借助幾何畫板演示，觀察得知直線l過定點.由題意知橢圓右頂點為P(2,0)，設A(x1,y1),B(x2,y2)，則

y=k(x-2)+2k+m.

若2k+m=0,則l過定點(2,0),這與已知矛盾,故2k+m≠0,直線方程可變形為

(7)

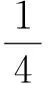
即 3(x-2)2+12(x-2)·1+4y2=0.

(8)

將式(7)代入式(8),得

整理得

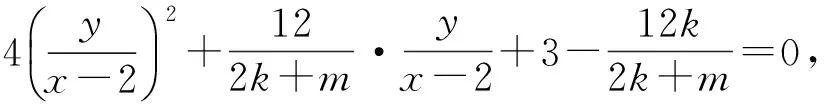
解得

例3求經過2個圓：x2+y2+6x-4=0和x2+y2+6y-28=0的交點且面積最小的圓的方程．

解易知所求圓為以2個已知圓公共弦為直徑的圓．2個圓方程為

式(9)-式(10)，得公共弦所在的直線方程為

由式(9)，式(11)分別消去y,x得

x2+7x+6=0,y2-y-6=0，

2式迭加得

x2+y2+7x-y=0,

圖4

即為所求圓的方程.

解設橢圓的方程為ax2+by2=1(a>0,b>0,a≠b).由y=x+1及ax2+by2=1分別消去y，x得

式(12)，式(13)相加，得以PQ為直徑的圓的方程為

(a+b)x2+(a+b)y2+2bx-2ay+a+b-2=0.

(14)

由于OP⊥OQ,故該圓過原點(0，0),即a+b=2，代入式(14)，得

x2+y2+bx-ay=0,

即

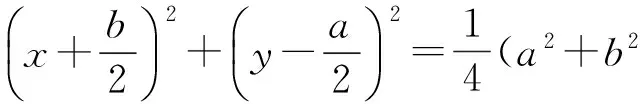
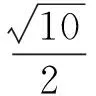
即

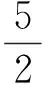
又由a+b=2，可解得

故所求的橢圓方程為

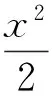
課本和各種教學參考書為我們提供了大量的有價值的典型題目，這些題目具有入口寬、解法多、綜合性強、考查面廣的特點，其解法往往可以拓展應用到其他題型中去.這些典型題目備受各類考試命題者的青睞，成為各類考試的“題源”.因此，有必要經常對這些典型題目的解法加以拓展探究.只要堅持下去，必將收到舉一反三、以少馭多的效果.

[1] 李愛生.教材原題多解探究[J].考試(高考·試題設計)，2011(5):16-19.

浙江省初、高中數學新課程“疑難問題解決”專題研討會分別在嘉興、余姚舉行

2011年浙江省初、高中數學新課程“疑難問題解決”專題研討會于11月下旬分別在嘉興實驗初中和余姚中學順利舉行。本次活動由浙江省教育廳教研室、浙江省數學會主辦，浙江省各地市初、高中數學教研員、數學骨干教師500余人參加了此次活動。浙江師范大學期刊社副社長、《中學教研》(數學)主編張翼教授出席了此次會議，加強了我刊與中學數學界的聯系與交流。本次會議的主題是初、高中數學課堂教學目標的有效設計與落實及其疑難問題的解決。旨在幫助一線教師進一步提升解決課程改革中疑難問題的能力，推動初、高中數學新課程的深入實施。會議形式豐富，安排緊湊，內容充實，實實在在地解決了一線教師在課程改革中遇到的一些疑難問題，使參與培訓的教師開闊了眼界、收獲了智慧，促進了教師的教學實踐與研究，并將有效地推動我省初、高中數學教學水平的提升。