一道自主招生試題的解法探究

●

(盱眙中學 江蘇淮安 211700)

一道自主招生試題的解法探究

●周志國

(盱眙中學 江蘇淮安 211700)

題目已知數列{an},{bn}滿足an+1=-an-2bn，且bn+1=6an+6bn，又a1=2，b1=4，試求數列{an},{bn}的通項公式．

(2004年復旦大學自主招生數學試題)

這是一道魅力無窮的自主招生試題！下面筆者給出它的奇妙多解.

1 眾里挑一，各個擊破.

當2個不同的數列雜糅在一起時，關系不明確，很難認清.筆者嘗試利用解方程的思想，尋求某一個數列的遞推關系，顯現出數列各自的特征，便于深入認識數列.基于此，筆者給出了如下幾種解法．

方法1特征根法.

解由條件an+1=-an-2bn，得

從而

將bn+1，bn代入bn+1=6an+6bn，得

整理得

an+2=5an+1-6an，

其特征根方程為

x2-5x+6=0，

解得

x1=2,x2=3，

從而可設

an=c12n-1+c23n-1.

由a1=2,a2=-10得

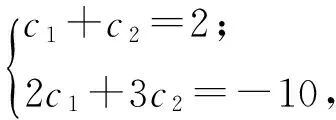
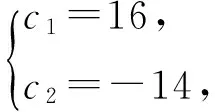
an=2n+3-14·3n-1，

故

點評方法1的關鍵是消元，要求學生從方程角度認識等式，轉化成某一數列連續3項的遞推關系，并熟悉用特征根法求通項的方法．

方法2待定系數法.

解由方法1知

an+2=5an+1-6an,

令an+2-λan+1=μ(an+1-λan)，則

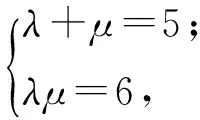
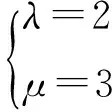
或an+2-3an+1=2(an+1-3an)，

得

an+1-2an=-14·3n-1,

(1)

an+1-3an=-2n+3,

(2)

由式(1)，式(2)得

an=2n+3-14·3n-1,bn=28·3n-1-3·2n+2.

點評將an+2=5an+1-6an轉化成熟悉的2項間的遞推是本問題的關鍵，嘗試通過化歸，抓住整體特征，待定系數，轉化成熟悉的2項間的遞推，再通過解方程組，求出數列{an}，{bn}的通項公式．

方法3化歸為特殊數列.

解由方法2知

an+1-2an=-14·3n-1，

從而

故

an=2n+3-14·3n-1,bn=28·3n-1-3·2n+2．

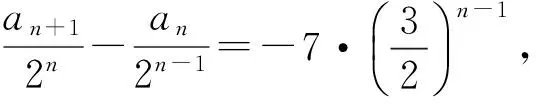
2 順水推舟，層層深入.

已知多個數列雜糅的遞推關系式，求數列通項公式，解決這類問題的關鍵是能否準確把握遞推關系式的結構，注意關系式的整體結構，構造新數列，層層深入，突破難點，求出通項公式．

方法4構造新數列.

解令an+1+λbn+1=μ(an+λbn),

(3)

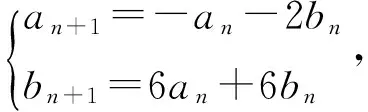
an+1+λbn+1= (-an-2bn)+λ(6an+6bn)=

(6λ-1)an+(6λ-2)bn,

(4)

比較式(3)，式(4)得

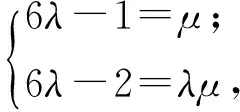
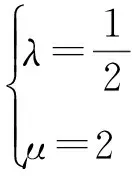
從而

2an+1+bn+1=2(2an+bn)，

或 3an+1+2bn+1=3(3an+2bn).

利用等比數列的定義可得

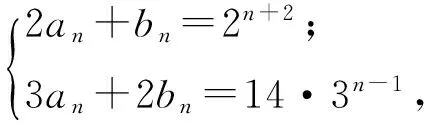
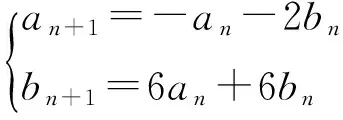
方法5利用矩陣變換.

解由題意得

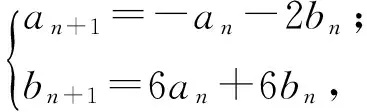
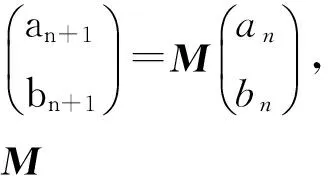
故特征值λ1=2，λ2=3，對應的特征向量分別為

設β=mα1+nα2，m,n∈R，可得m=8,n=-14，

即

β=8α1-14α2，

于是

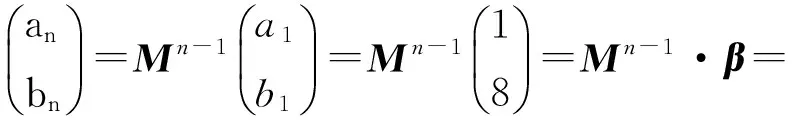
即

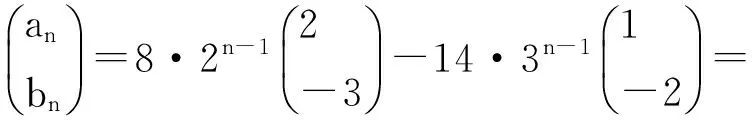
an=2n+3-14·3n-1,bn=28·3n-1-3·2n+2．

該題初看難以入手，仔細研究就會發現，試題內涵深厚，縱橫聯系．該題的5種方法，以數學思想方法引領，從不同的角度切入，應用不同的數學知識，顯現出不同的精彩，給人以美的享受．最后以著名的數學教育家波利亞的一句話與大家共勉：沒有一道題可以解決得十全十美，總存在值得我們探究的地方．

[1] 楊蒼洲．解題，從結構聯想開始[J]．數學通訊，2011(4)：14-16．

[2] 吳旭紅．高中數學選修內容運用例析[J]．中學數學月刊，2009(11)：40-42．