一道平面幾何競賽題的多解性討論

●

(紹興市第一中學 浙江紹興 312000)

一道平面幾何競賽題的多解性討論

●凌曉鋒

(紹興市第一中學 浙江紹興 312000)

一道優秀的平面幾何題往往可以從不同的知識層面去考查學生運用所學知識分析并解決問題的能力,2011年浙江省高中數學競賽第21題(附加題)便是這樣一道具有多解性的好題.本文將用平面幾何方法、三角參量法、解析法以及面積法等4種不同的方法對其多解性展開討論,以饗讀者.

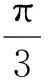
(2011年浙江省數學競賽試題)

1 標準答案再現

作△ABC的外接圓O,然后作OE⊥AB于點E,OF⊥AC于點F,OM⊥BC于點M,則四邊形AEOF即為區域G.因為

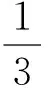
2S四邊形AEOF=2S△AOE+2S△AOF=S△AOB+S△AOC，

所以

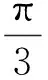
作AD⊥BC于點D,則

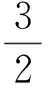
當且僅當點A，O，M共線時等號成立,即△ABC為等邊三角形.

點評上述方法根據已知條件等價轉換成面積關系,然后利用三點共線使面積取到最值,從而證明了結論.證明過程簡潔明了,一氣呵成,但是筆者在閱卷過程中鮮有發現學生用此類方法證明.下面筆者給出其他3種不同的證明方法.

2 三角參量法

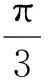
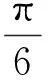
從而

S四邊形ADOE=S△AOE+S△AOD=

又因為

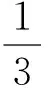
所以

(1)

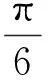
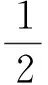
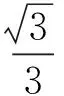
(2)

即

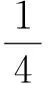
從而

化簡得

cos2θ=1.

因為

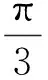
所以

2θ=0，

即

θ=0,

從而

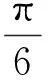
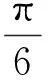
即

AC=2b=2c=AB,

從而

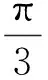
故△ABC為等邊三角形.

點評以上證法通過設參數角θ,利用已知條件的面積關系,列出三角函數方程.經過一系列三角恒等變換確定參數角θ的值,最后轉而求得邊長的關系,從而使命題得證.求解平面幾何的問題,常引入線段、角度、面積、比值等作為參量.在引入角度參量后，往往運用三角知識,進行三角運算以及運用正弦、余弦定理等來溝通幾何與三角的關系，這種求解平面幾何問題的方法稱為三角參量法.

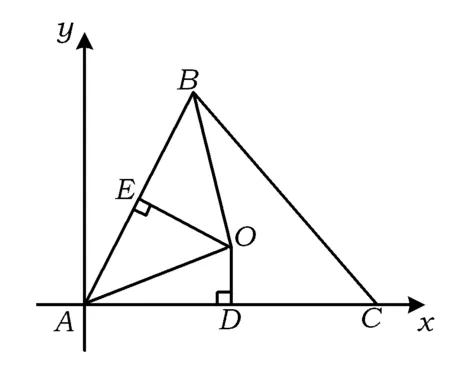
圖1

3 解析法

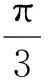
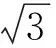
因為OE為AB的中垂線,所以

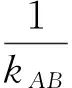
OE的解析式為

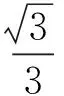
又因為D為AC的中點,所以OD的解析式為

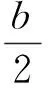
因為

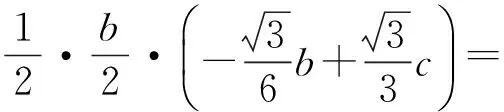
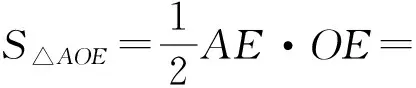
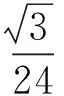
(3)

(4)

由式(3),式(4)得

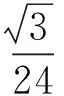
化簡得

b2-4bc+c2=-2bc,

即

(b-c)2=0,

從而

b=c,

即

AC=2b=2c=AB,

故

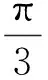
因此△ABC為等邊三角形.

點評利用建立平面直角坐標系,通過數形結合的思想,求出各點的坐標,利用已知性質求得結果,這種方法思維過程較為直接,在這里有較高的使用價值.利用解析法的關鍵是,選擇適當的坐標系，同時還要靈活利用幾何圖形的性質及代數、三角知識的綜合運用.

4 面積法

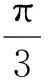
即

從而

S△AOB+S△AOC=2S△BOC,

即

化簡得 sin∠AOB+sin∠AOC=2sin∠BOC,

即

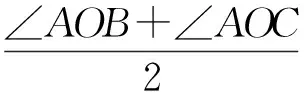
(5)

又

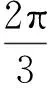
從而

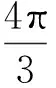
代入式(5)得

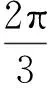
從而

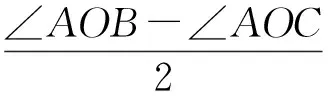
得

∠AOB-∠AOC=0,

即

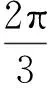
故

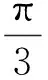
因此△ABC為等邊三角形.

點評在求解平面幾何問題的時候,根據幾何量與有關圖形面積之間的內在聯系,用面積表示有關幾何量,從而把要論證的幾何量之間的關系化為有關面積之間的數量關系,特別是利用面積公式,得到三角函數方程,通過三角恒等變換求解問題,使得幾何證明的過程機械化,這一思想頗為重要.

通過以上討論,筆者認為雖然平面幾何這塊內容學生主要是在初中階段打下的基礎,但是作為高中數學競賽中的一塊重要內容,在平時教學過程中教師可以結合高中的三角函數、解析幾何、平面向量等知識的運用，去引導學生拓展思路,一題多解,從而使平面幾何問題的優美性和精巧性得以充分地展現.

[1] 沈文選.平面幾何證明方法全書[M].哈爾濱：哈爾濱工業大學出版社，2005：76-84.

關于征訂《中學教研》(數學)高考復習專輯啟事

各位老師、高三同學：

為滿足廣大高三師生高考復習備考的需求，本刊特在第2期推出高考復習專輯(2012年2月5日前出版)。本專輯以數學思想和方法作為數學高考復習主線，主要包括函數與方程、數形結合、分類、化歸等重要的思想方法，結合考點分析命題走向，設有典型例題解讀、精題集萃、模擬試題等板塊。

本專輯由浙江省教研室高中數學教研員、中學數學特級教師張金良老師組稿，并邀請了特級教師馬茂年、蔣榮清、鄭日鋒、賴忠華等一批具有豐富高考經驗的知名專家撰稿，并配有鎮海中學等知名學校編制的模擬試卷，具有極強的權威性、針對性和實用性，是廣大考生不可或缺的備考復習資料。

數學高考專輯(第2期)(單價:4元/本)冊數:訂書單位: 郵編:詳細地址:聯系人: 電話:總款數:

聯系電話：0579-82298829 E-mail: zxjysx@zjnu.cn