巧補(bǔ)形 妙解題

●

(晉州市實(shí)驗(yàn)中學(xué) 河北晉州 052260)

巧補(bǔ)形妙解題

●苑建廣

(晉州市實(shí)驗(yàn)中學(xué) 河北晉州 052260)

對(duì)于給定“非規(guī)則”圖形的數(shù)學(xué)題，通常不易打開(kāi)思路.這時(shí)可綜合考慮題設(shè)、結(jié)論及所給圖形的特征，通過(guò)“補(bǔ)形”將原圖形巧加完善，揭示本質(zhì)，釋放內(nèi)涵.由于我們對(duì)等腰三角形、直角三角形、等邊三角形、等腰梯形、矩形、菱形、正方形、圓等特殊圖形較為熟悉，因此，若能通過(guò)圖形變換或做輔助線把非規(guī)則圖形化歸為這些特殊圖形，則往往能夠化分散為集中，迅速找到解題方法.現(xiàn)歸類(lèi)例析，僅供讀者探究之用.

1 補(bǔ)成正三角形

例1如圖1，六邊形ABCDEF的6個(gè)內(nèi)角都相等．若AB=1，BC=CD=3，DE=2，則這個(gè)六邊形的周長(zhǎng)等于________.

(2011年天津市數(shù)學(xué)中考試題)

圖1 圖2

分析由于六邊形ABCDEF的每個(gè)內(nèi)角都相等(均為120°)，且每個(gè)頂點(diǎn)處的外角均為60°，這樣便容易想到將六邊形完善成正三角形.分別作邊AB，CD，EF所在的直線，并相交于點(diǎn)M，N，P.易判斷△MAF，△PDE，△NBC，△MNP均為正三角形，于是

NB=NC=BC=3，PD=PE=DE=2，

得

PN=NC+CD+PD=8.

由△MNP是邊長(zhǎng)為8的正三角形，得

MA=MN-NB-AB=8-3-1=4，

即

AF=FM=AM=4，

同理

EF=PM-FM-PE=8-4-2=2，

進(jìn)而可得六邊形ABCDEF的周長(zhǎng)為15.

例2如圖2，已知△ABC為等邊三角形，延長(zhǎng)BC到D，延長(zhǎng)BA到E，并且使AE=BD.聯(lián)結(jié)CE，DE,求證：EC=ED．

(2000年內(nèi)蒙古自治區(qū)數(shù)學(xué)中考試題)

分析直接通過(guò)推導(dǎo)∠ECD=∠EDC來(lái)證明EC=ED比較困難.此時(shí)可結(jié)合題、圖及結(jié)論特征，將原圖補(bǔ)成正三角形：延長(zhǎng)BD至點(diǎn)F，使DF=BC，聯(lián)結(jié)EF.因?yàn)锳E=BD，△ABC為等邊三角形，所以

BE=BF，∠B=60°，

從而△BEF為等邊三角形，得

∠F=60°，EB=EF.

又易知CB=DF，則

△EBC≌△EDF，

得

EC=ED．

2 補(bǔ)成直角三角形

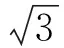
(2009年內(nèi)蒙古自治區(qū)呼和浩特市數(shù)學(xué)中考試題)

分析由AB⊥AD，BC⊥CD，知可將原圖補(bǔ)成直角三角形：延長(zhǎng)DA，CB交于點(diǎn)E，則∠ABE=60°，∠E=30°．在Rt△EAB中，

AB=4，∠E=30°，

得

BE=8，AE=4；

在Rt△DEC中，

CD=5，∠E=30°，

得

CE=15，

于是

因此四邊形ABCD的面積為

圖3 圖4

例4如圖4，在梯形ABCD中，AD∥BC，∠B+∠C=90°，AD=1，BC=3，E，F(xiàn)分別是AD，BC的中點(diǎn)，則EF=________.

(2004年江蘇省宿遷市數(shù)學(xué)中考試題)

分析由∠B，∠C互余，知可考慮將原圖補(bǔ)成直角三角形.延長(zhǎng)BA，CD，相交于點(diǎn)P，聯(lián)結(jié)PF.設(shè)PF與AD交于點(diǎn)E′，由AD∥BC，得

又由BF=FC，得AE′=DE′，即點(diǎn)E與點(diǎn)E′重合.在Rt△PBC中，有

在Rt△PAD中，有

于是

EF=PF-PE=1.

3 補(bǔ)成等腰三角形

例5如圖5，在梯形ABCD中，AD∥BC，CE是∠BCD的平分線，且CE⊥AB，E為垂足，BE=2AE.若四邊形AECD的面積為1，則梯形ABCD的面積為_(kāi)_______.

(2011年內(nèi)蒙古自治區(qū)呼和浩特市數(shù)學(xué)中考試題)

分析由已知條件“CE平分∠BCD”和“CE⊥AB”，結(jié)合等腰三角形“三線合一”，可想到延長(zhǎng)BA，CD相交于點(diǎn)F.易知△CBF為等腰三角形(CB=CF)，且BE=EF,故△CBE≌△CFE.設(shè)AE=a，則BE=EF=2a，AF=a.

另設(shè)△CBE的面積為S，則△FAD的面積為S-1，△CBF的面積為2S.由△FAD∽△FBC，得

圖5 圖6

例6如圖6，在等腰梯形ABCD中，AD∥BC，∠C=60°，AD=10，AB=18，求BC的長(zhǎng)．

(2005年海南省數(shù)學(xué)中考試題)

分析分別延長(zhǎng)BA，CD交于點(diǎn)E．由

AD∥BC，AB=CD，得

∠B=∠C=60°，∠EAD=∠EDA=60°，

從而△EBC與△EAD均為等邊三角形，得

BC=BE=AB+AE=AB+AD=18+10=28．

4 補(bǔ)成正方形

例7如圖7，在△ABC中，∠BAC=45°,AD⊥BC于點(diǎn)D，已知BD=6,CD=4,則高AD的長(zhǎng)為_(kāi)_______．

(2008年湖北省鄂州市數(shù)學(xué)中考試題)

分析由∠BAC=45°，可聯(lián)想到完善圖形:作△ABD關(guān)于AB對(duì)稱(chēng)的△ABM，再作△ACD關(guān)于AC對(duì)稱(chēng)的△CAN.延長(zhǎng)MB，NC交于點(diǎn)P，易知四邊形AMPN是正方形.若設(shè)AD=x，則正方形的邊長(zhǎng)等于x，BP=MP-MB=x-6，CP=NP-NC=x-4.在Rt△BCP中，有

(x-6)2+(x-4)2=(6+4)2，

解得x=12，即高AD=12.

圖7 圖8

5 補(bǔ)成矩形

例8同例1.

分析如圖8，過(guò)點(diǎn)B作AF的垂線，分別交AF，CD所在的直線于點(diǎn)M，N；再過(guò)點(diǎn)E作AF的垂線，分別交AF，CD所在的直線于點(diǎn)P，Q.易知四邊形MNQP為矩形.

在Rt△MAB中，AB=1，∠MAB=60°，可得

同理，在Rt△NBC中，可得

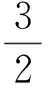
在Rt△QDE中，可得

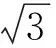
因此

MP=NQ=NC+CD+QD=

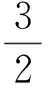
又

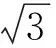
得

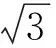
在Rt△PEF中，由∠PEF=60°，得

EF=2，PF=1,

從而

因此六邊形ABCDEF周長(zhǎng)為15.

6 補(bǔ)成菱形

例9如圖9,在凸五邊形ABCDE中，∠A=∠B=120°，EA=AB=BC=2，CD=DE=4，則它的面積為_(kāi)_______.

(第44屆美國(guó)AHSME試題)

分析結(jié)合題、圖特征，容易想到補(bǔ)全原圖形為菱形：延長(zhǎng)EA，CB交于點(diǎn)F.易知△FAB為正三角形，邊長(zhǎng)為2,四邊形FCDE為菱形，邊長(zhǎng)為4.于是

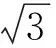
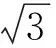
圖9 圖10

7 補(bǔ)成平行四邊形

例10同例1.

分析如圖10，延長(zhǎng)FA，CB交于點(diǎn)M，延長(zhǎng)FE，CD交于點(diǎn)N.易知△MAB，△NDE均為正三角形，且四邊形MCNF為平行四邊形.從而

MB=MA=AB=1，EN=ND=ED=2，

于是

MC=MB+BC=1+3=4.

因?yàn)樗倪呅蜯CNF是平行四邊形，所以

FN=MC=4，

得

EF=FN-EN=4-2=2.

同理可得AF=4，則六邊形ABCDEF的周長(zhǎng)為15.

圖11 圖12

例11同例6.

分析如圖11，過(guò)點(diǎn)C作CE∥BA交AD的延長(zhǎng)線于點(diǎn)E．易知四邊形ABCE是平行四邊形，△DEC是等邊三角形，則

DE=DC=AB=18，

從而

BC=AE=AD+DE=10+18=28．

例12如圖12，在四邊形ABCD中，AB=CD，M，N，P，Q分別是AD，BC，BD，AC的中點(diǎn)．求證：MN與PQ互相垂直平分．

(2007年湖南省株洲市數(shù)學(xué)中考試題)

分析欲證MN與PQ互相垂直平分，則四邊形MPNQ必為菱形.聯(lián)結(jié)MP，PN，NQ，QM，補(bǔ)全成菱形,由

AM=MD，BP=PD，

得

從而

PM=NQ，且PM∥NQ，

即四邊形MPNQ是平行四邊形.又由AB=DC，可得

PM=MQ，

從而平行四邊形MPNQ是菱形,MN與PQ互相垂直平分．

8 補(bǔ)成等腰梯形

例13同例1.

圖13

分析如圖13，延長(zhǎng)AB，DC交于點(diǎn)M，延長(zhǎng)FE，CD交于點(diǎn)N，過(guò)點(diǎn)A作AP∥FN交MN于點(diǎn)P.易知四邊形AMNF為等腰梯形，△MBC，△MAP，△NDE是正三角形，四邊形APNF為平行四邊形，且AM=FN=4，MN=8,于是

MP=AM=4，

PN=MN-MP=8-4=4，

從而

AF=PN=4.

又EN=DE=2，得

EF=FN-EN=4-2=2，

因此原六邊形周長(zhǎng)為15.

9 補(bǔ)成圓

圓有著許多美妙的性質(zhì).不少數(shù)學(xué)難題,通過(guò)構(gòu)造“輔助圓”往往能出奇制勝.

例14如圖14，在四邊形ABCD中，AB=AC=AD.若∠CAD=76°，則∠CBD=________.

(2008年山東省濟(jì)寧市數(shù)學(xué)中考試題)

圖14 圖15

例15如圖15，若PA=PB，∠APB=2∠ACB，AC與PB交于點(diǎn)D，且PB=4，PD=3，則AD·CD

等于________.

(2001年TI杯全國(guó)初中數(shù)學(xué)競(jìng)賽題)

分析看到“PA=PB”和“∠APB=2∠ACB”，容易想到：以點(diǎn)P為圓心、PA長(zhǎng)為半徑作圓.此時(shí)，點(diǎn)C必然落在⊙P上.作直徑BT，聯(lián)結(jié)AT,則BT=8，TD=7，BD=1.易證△BCD∽△ATD,則

即

AD·CD=TD·BD=7.

由此可見(jiàn)，巧妙“補(bǔ)形”，能把條件化分散為集中，便于整體思考和運(yùn)用，可以迅速釋放題、圖內(nèi)涵，打開(kāi)解題思路.這一點(diǎn)提示我們，遇到平面幾何問(wèn)題時(shí)，要善于借助各種手段把不規(guī)則、不標(biāo)準(zhǔn)、不熟悉的圖形向規(guī)則、標(biāo)準(zhǔn)、熟悉的圖形轉(zhuǎn)化，從而溝通條件和結(jié)論之間的聯(lián)系，化生為熟，化難為易.