數學課堂教學的“真”、“善”、“美”

●

(義烏中學 浙江義烏 322000)

數學課堂教學的“真”、“善”、“美”

●朱恒元

(義烏中學 浙江義烏 322000)

如果說概念課強調的是基礎和全面，那么習題課側重的是重點和提高.后者教學的通常做法是羅列一些知識點和“七方八法”，讓解題“對號入座”，這就容易出現“炒冷飯”、“走過場”的教學現象.其原因何在？原來是我們的課堂教學過于飽和求“真”，而沒有充分展現數學問題和教學的“善”與“美”.其實，缺了“善”，學生的思維密度低，提不起精神，過早出現“高原反應”；少了“美”，學生學習興趣弱，感到學習就是做題，容易產生“視覺疲勞”.數學的理性思維活靈活現，數學的以美啟真熠熠生輝，關鍵是我們怎樣去點擊，怎樣去碰撞.

筆者曾在義烏市高中數學教研活動中上過一堂“直線與圓錐曲線相切問題”的公開課.試想從這節課的教學展開，簡談數學課堂教學如何追求“真”、“善”、“美”的實踐和認識.

圖1

1 一堂課的教學實錄

師：請同學們談一談解題思路.

生2：設切點為P(x0,y0)，則切線的斜率

從而求得點P的坐標.

師：生1給出的是一般性、通用性的方法；生2給出的是技巧性、靈活性的方法.

學生演算，教師巡視，一會兒請3位學生代表進行板演(把演算結果的主干部分抄錄在黑板上).

生3：用方程組的通法解(這里略).

得x0=4，故P(4,-4).

師：生4、生5都利用了導數求解，但結果不同，誰是誰非呢？

生6：生5是正確的，結果也與生3一致.生4解錯了，因為我們說的導數是“函數的導數”，所應用的求導公式是“y對x的求導”，因此，必須先求得y關于x的函數表達式.

師：這位同學的分析鞭辟入里，很好.雖然生5的解法是正確的，但格式的規范還可以改進.根據生6的看法，可利用導數求解這類問題，一般有“選段”、“改寫”、“求導”三步曲.其中的選段，就是在曲線上選取一段，使之能成為某個函數的圖像；改寫，就是寫出選取圖像所對應的函數表達式(y關于x的函數表達式)，它是曲線方程的改變形式；求導，就是應用所學的求導公式進行“y對x的求導”.

圖2

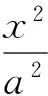
(1)求橢圓方程；

學生迅速完成第(1)小題的解答：

師：對于第(2)小題，不失一般性，不妨設點P在第一象限.同學們自己試解一下.

片刻，選2位學生代表進行板演(把演算結果的主干部分抄錄在黑板上).

生7：設過點P的切線方程為

y=y0+k(x-x0)，

(1)

由條件可得此方程有2個相等的實根，故

Δ=1+4k2-(y0-kx0)2=0.

生7解題受阻.

從而

又由條件，得

于是

故

圖3

生9：不失一般性，不妨選取橢圓在第一象限的部分(如圖3)，則圖像所對應的函數表達式為

設切點P的坐標為(x0,y0)，則

從而

于是

即

因此

師：在這里，生9的解法就有明顯的優勢.看來，思路、方法和技巧構成了數學解題的一個系統工程，有必要加以關注.

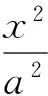
4）數字化資源則指的是各種慕課平臺提供的資源和高校開發、建設的大量網絡課程、微課、慕課等，主要為學生在課下自主學習和課程交流協作學習提供學習資源。

(1)求橢圓方程；

圖4

讓學生們試解，再把生10和生11的演算結果用投影儀展示出來.

解法1(1)過點A，B的直線方程為

Δ=a2b2(a2+4b2-4)=0(ab≠0)，

故

a2+4b2-4=0.

a2=4b2.

從而

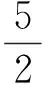
解法2(1)選取橢圓在第一象限的部分，則圖像所對應的函數表達式為

設切點T的坐標為(x0,y0)，則

得

從而

代入直線方程得

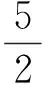
因此

教學片斷4

生12：取線段AF2的中點為M，可得

|AT|2=|AF1|·|AM|.

師：很好！請同學們由此觀察，你發現圖形有哪些特點，得出什么結論？

學生的興致很濃，你一言我一語，最后發現：△ATM與△AF1T相似(因為對應邊成比例且夾角相等)，得出結果：∠ATM=∠AF1T.于是問題3的變化題也就“應運而生”了.

圖5

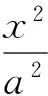
(1)求橢圓方程；

(2)設F1，F2分別為橢圓的左、右焦點，M為線段AF2的中點，求證：∠ATM=∠AF1T.

師：剛才，我們編擬出了一道變化題，并給出了一種解答，但總覺得平面幾何的味道太濃.請大家再思考一下，拿出一個最優解法來.

所以

∠ATM=∠AF1T.

師：這位同學運用傾斜角、斜率和三角函數的正切公式等知識解決了問題，思路非常清晰！

2 課堂教學的“三維目標”

2.1 真——知識在變式訓練和辨析糾錯中鞏固

對于直線與二次函數型拋物線相切的問題1，學生平時訓練有素，通法技法運用自如.但我們想“大海掀起波瀾”、“樂章開始變奏”，在教學片斷1變式練習中“引蛇出洞”，著重糾正對“函數的導數”概念的錯誤理解.通過辨析“方程的曲線”和“函數的圖像”的聯系與區別，使技法的“生命”得到延續，讓技法的操作更程式化.我們利用導數求解這類問題，一般有“選段”、“改述”、“求導”三步曲.解題過程中讓學生口述三步曲的3個關鍵詞：“選段”、“改述”、“求導”，以給學生耳目一新的視覺沖擊.

2.2 善——方法在深刻理解和理性選擇中優化

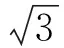
教學片斷3中的問題3是2006年浙江省數學高考文科試題，在解答第(1)小題時，用求導的方法并不見得好些.通過這個良好的教學載體，無非是要表明“通性通法屬首選，技法巧法也要會”的教學主張.我們在教學中還進一步強化了格式的規范性和步驟的嚴謹性.

2.3 美——能力在返璞歸真和直覺頓悟中提升

對教學片斷4中問題3第(2)小題結果的再審視，它是本節課教學的重頭戲.通過對結果的“求美”，我們有了一系列的教學發現，編擬出了問題3的變化題(這是2006年浙江省數學高考理科試題)，讓學生享受到了成功的喜悅.在順水推舟中，用平面幾何知識解決了此題.但此時教師及時給學生“潑了盆冷水”(總覺得平面幾何的味道太濃)，引導學生尋求運用傾斜角、斜率和三角函數的正切公式等知識加以解決.這可不是簡單的“一題多解”，而是數學學習的“返璞歸真”，讓學生始終把握住解析幾何的本質——用代數的方法研究幾何的性質！

朱恒元，1962年生，浙江義烏人，中學高級教師.1980年參加教育工作.曾任浙江省教育廳教研室高中數學教研員，現為金華市數學會副會長兼學術委員會主任.先后在《數學通報》等報刊上發表教研文章100余篇，其中被中國人民大學書報資料中心《高中數學教與學》全文轉載10篇.先后被評為(獲得)金華市拔尖人才、浙江省名師首批培養人選、教育部中小學骨干教師國家級培訓對象、浙江省特級教師、全國“蘇步青數學教育獎”.