基于球形固結模型的樁端后注漿殘余應力理論研究

張忠苗，何景愈,，房 凱

（1.浙江大學 巖土工程研究所，杭州 310058；2.浙江大學 軟弱土與環境土工教育部重點實驗室，杭州 310058；3.廣西壯族自治區南寧市城鄉建設委員會，南寧 530029）

1 引 言

樁端后注漿是指鉆孔灌注樁在成樁后，采用高壓注漿泵將一定壓力的水泥漿經預埋的注漿通道壓入樁端土層，通過增強樁端土和樁側土的強度來提高樁基極限承載力、減少群樁沉降量的一項技術措施[1－2]。研究表明，樁端后注漿會產生殘余應力，并對后注漿樁承載性狀產生影響[3]。迄今為止，國內外對樁端后注漿殘余應力的研究很少，僅知道殘余應力會對后注漿樁極限承載力、側摩阻力和端阻力造成一定的影響，嚴重時會引起樁體或管線的上抬[3－8]。

灌注樁在注漿過程中高壓漿液對樁端土體產生很大的壓力，在周圍土體中產生超孔隙水壓力，注漿結束后注漿壓力不能及時消散，會在樁端產生殘余應力，在壓力的作用下引起樁端土的固結，孔隙水壓力逐漸消散，土體有效應力逐漸增長。同時，樁端土中孔壓的消散過程也是樁端殘余應力消散的過程。

本文在球形空腔擴張及一維徑向固結理論的基礎上，對樁端后注漿樁的樁端注漿殘余應力進行理論研究，在負指數衰減的初始超靜孔隙水壓力分布基礎上，得到了殘余應力隨時間及擴散半徑消散的解析解，同時對模型的主要影響參數進行了分析。實測數據表明，該解析解能有效地模擬后注漿殘余應力的消散，研究結果對后注漿殘余應力的理論研究及工程實踐有重要的指導意義。

2 數學模型的建立

2.1 初始時刻注漿殘余應力的分布

樁端后注漿漿液的擴散機制及注漿壓力的分布是十分復雜的，是目前仍待研究的課題[1]。要精確地考慮注漿壓力隨時間及擴散半徑的變化將使問題變得極其復雜，并難以求解。本文按照下述初始超靜孔隙水壓力的分布規律來簡化模擬注漿結束時漿液擴散半徑范圍內注漿殘余應力的分布。

Vesic[9]提出球形空腔擴張引起的初始超靜孔隙水壓力可用下式來估算：

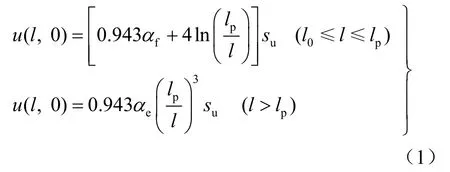
式中：su為土體不排水強度；u(l,0)為由球形空腔擴張引起的超靜孔隙水壓力；l為相應點到孔中心的距離；l0為空腔擴張半徑，即注漿管半徑，一般為0.03～0.05 m；lp為塑性區半徑；αf為破壞時的Henkel孔隙水壓力參數；αe為Henkel孔壓彈性系數。

式（1）雖然考慮了土體中塑性區的影響，但利用時需要測定較多的土工參數，故式（1）不便于實際的工程應用。朱小林等[10]也曾指出，超孔隙水壓力的初始分布并不完全符合式（1）所示的對數型衰減規律，而更可能符合負指數型衰減：

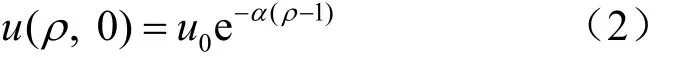
式中：α為正值，一般取0.15～0.40之間，α宜取高值[10]，且α取0.3～0.4對初始孔壓分布影響不大；ρ為徑向距離比，ρ=l/l0；u0為空腔l0處初始超靜孔隙水壓力，此處為注漿結束時注漿管端處的殘余應力值。

2.2 殘余應力消散的固結微分方程

注漿結束后，注入樁端漿液因滲透和壓濾作用而逐漸消散。注漿殘余應力，即超孔隙水壓力以注漿管端為中心向四周消散，周圍的土體經歷著一個固結過程。假設土為理想均勻各向同性飽和土體，這一課題屬球空腔固結課題。為了能得到該問題的解答，作如下的假設和簡化：

（1）土體為理想均勻各向同性彈性飽和土體；

（2）土顆粒和孔隙水在固結過程中體積是不可壓縮的，土體固結變形為小變形；

（3）只考慮徑向滲流和位移，忽略豎向滲流和位移的影響，土中孔隙水的滲流服從達西定律；

（4）固結過程中，整個研究區域的固結系數及滲透系數相同且保持不變；

（5）注漿漿液為冪律流體，漿液在擴散及衰減過程中處于層流運動；

（6）注漿持續時間t′內，注漿壓力以球形方式向四周均勻擴散，初始殘余應力分布服從負指數型衰減。

在上述假設的基礎上，任意排水條件下的土體中球空腔固結微分方程可以表示為如下數學形式：

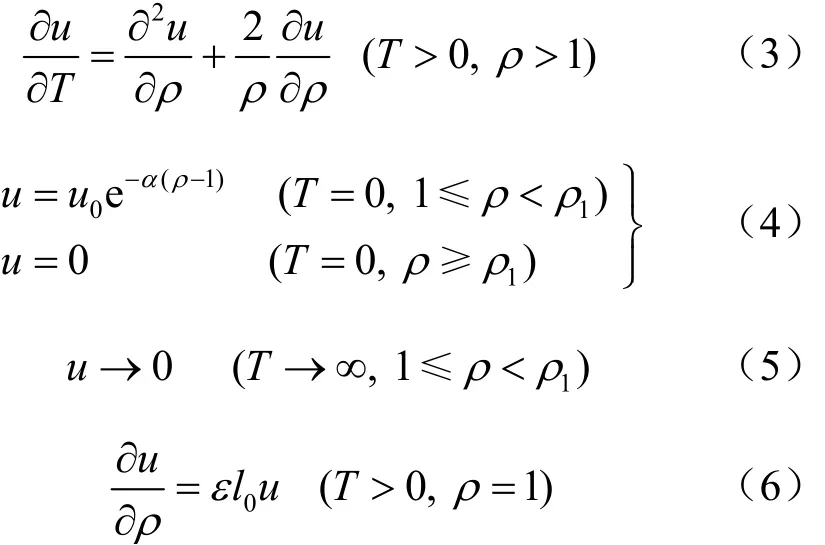
式中：T為時間因素，且 T=ct/(l1-l0)2，對樁端后注漿來說，漿液在樁端有一個擴散半徑l1，認為是注漿的影響半徑，在該范圍以外認為孔隙水壓力等于該地層的初始水壓力，不產生超孔壓，故時間因素T的計算公式中的排水路徑取為l1-l0；c為土體固結系數，c=Esk/γw，Es為土體的壓縮模量，k為土體的滲透系數，γw為水的重度；t為固結時間，即殘余應力的消散時間；ε為孔壁處邊界透水系數（ε=0，為不透水；0＜ε＜∞，為半透水；ε=∞為透水）。ρ1=l1/l0，l1為注漿漿液經過注漿持續時間t′后漿液最終擴散半徑，按照不同的流型及漿液流體可推出不同的漿液擴散半徑公式，根據以往的工程經驗，注漿漿液水灰比一般取 0.5～0.8[11]，該水灰比范圍水泥漿可認為是冪律流體[12]，l1可按下式確定，具體推導過程可參見楊秀竹等[13]的研究：

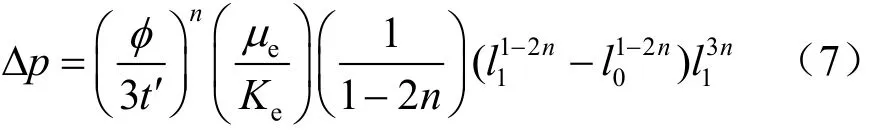
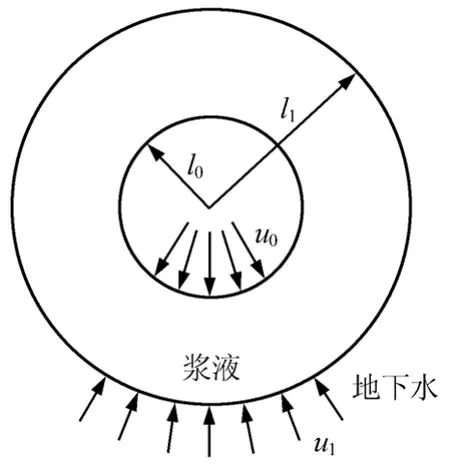
圖1 漿液球形擴散理論模型Fig.1 Spherically spreading model of grout

2.3 模型的求解

微分方程組式（3）～（6）一般可用分離變量法進行求解。

令V(ρ,T)=Γ(T)?R(ρ)=ρu(ρ,T)，Γ(T)、R(ρ)分別為T與ρ的單值函數，經過一系列地推導，可得到方程的解答如下，推導過程可參見朱小林等[10]的研究：

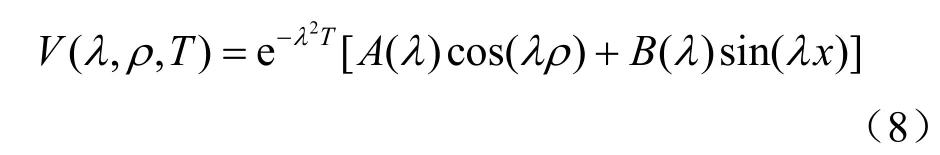
式中：λ為任意正實常數；A(λ)=(1+εl0) C(λ)、B(λ)=λC(λ)、C(λ)為λ的任意函數，由初始條件確定。

式（8）的全部解為按λ在區間(0,∞)內的積分疊加，即

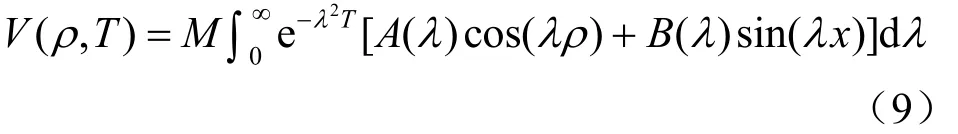
式中：M為任意常數，令M=1/π，結合初始條件V (ρ,0)=f (ρ)，則有

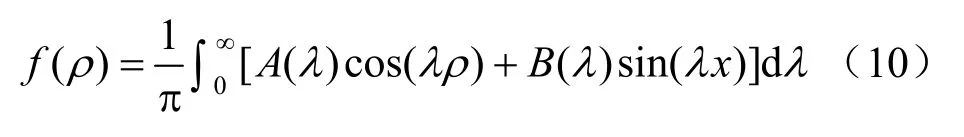
簡化后，式（9）可轉換為

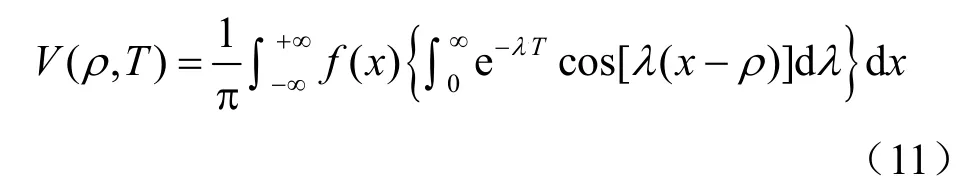
上式在轉換過程中，為避免混淆，已將余弦和正弦變換中的變量ρ換成為 x，花括號內的積分式可由下式確定：

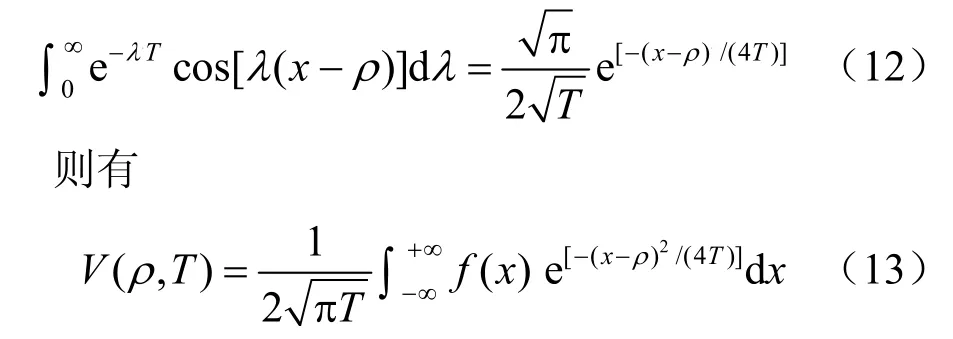
代入初始條件式（4），因式（4）是定義在[1,+∞)的范圍內的，為求解式（13）在(-∞,+∞)范圍內的積分，可按照解析開拓原理將式（4）所確定的函數解析開拓到整個(-∞,+∞)區域內，即

3 簡化算法

若不考慮漿液擴散半徑的影響，則式（14）為

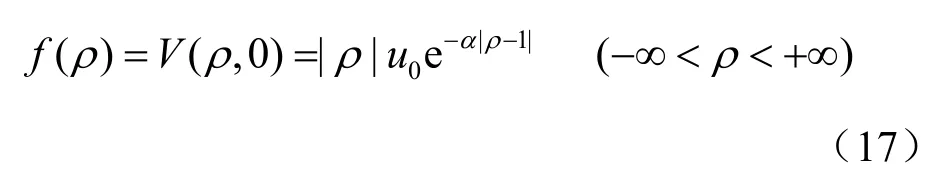
朱小林等[10]給出了式（13）的另一個解答，為

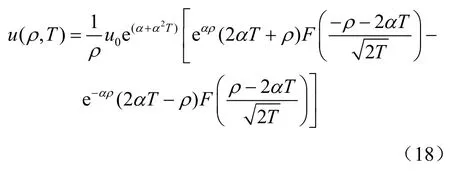
按式（18）可繪出注漿殘余應力隨距離和時間變化的規律，如圖2所示。

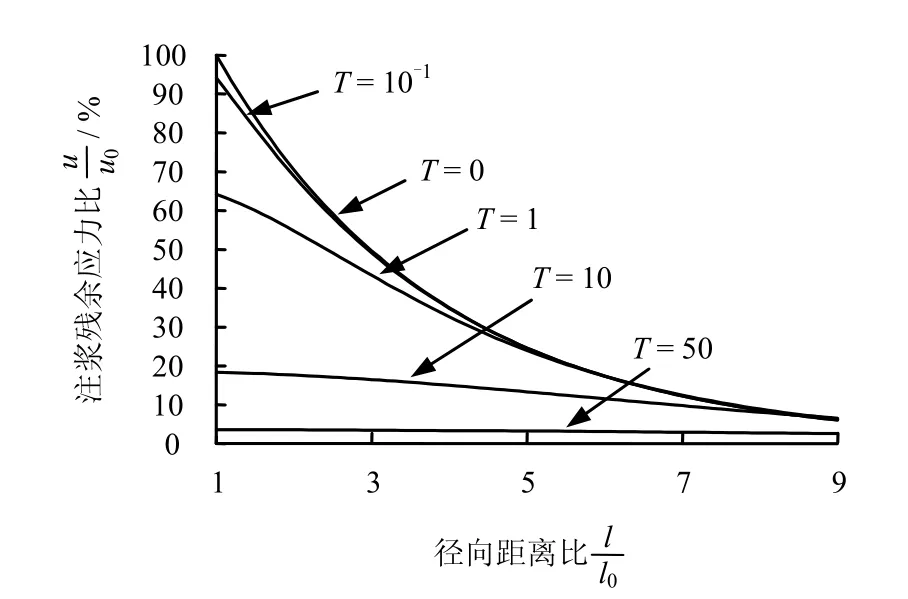
圖2 注漿殘余應力隨時間與徑向距離比的變化Fig.2 Variation curves of residual stress with time and radial distance ratio

從圖中可以看出，代表不同固結階段（T分別等于0、1 0-1、1、10、50）的各條曲線，在ρ=9處基本上已匯交。可以認為，ρ＞9及更遠處注漿殘余應力在整個固結過程中基本上沒有變化，隨著固結的持續，最終趨向于0。

4 參數分析

根據以上模型推導過程，影響注漿殘余應力的主要因素有流變指數 n、冪律流體的稠度系數 C、土體的滲透系數k、土體的壓縮模量Es、注漿持續時間t′及固結時間t。這6個參數都有明確的物理意義，可在實際試驗中測得，對6個主要因素進行分析，并對比本文及簡化算法，結果如圖3～8所示。

從圖3可以看出，流變指數n對注漿殘余應力影響較大，兩種方法的計算結果都隨流變指數n的增大而迅速減小；徑向距離比為1處，隨著流變指數n從0.15增加到0.40，本文算法計算注漿殘余應力比的結果從 89.68%減小到 65.21%，而簡化算法結果則從 81.55%減小到 21.63%，可見簡化算法結果隨流變指數增大的減少幅度更大。

從圖4可以看出，稠度系數C對注漿殘余應力也有較大的影響，兩種方法的計算結果都隨C的增大而減小；徑向距離比為1處，隨著C從0.15增加到 0.40，本文算法計算結果從 89.68%減小到71.00%，而簡化算法結果則從 55.10%減小到24.74%。

從圖 5中可以看出，隨著滲透系數 k從1.1×10-5m/s減小到 1.1×10-7m/s，兩種算法計算注漿殘余應力比的結果變化不大，但隨著 k從1.1×10-7m/s減小到1.1×10-9m/s，簡化算法計算的結果變化還是很小，而本文算法計算結果則發生了較大的變化，如徑向距離比為1處，本文算法計算結果從89.68%減小到43.23%。

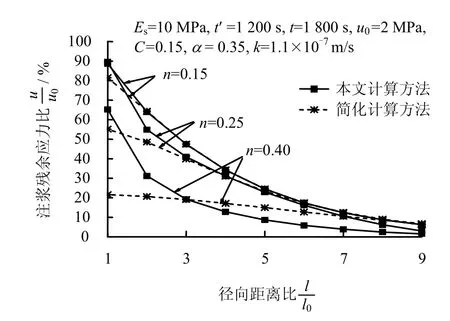
圖3 流變指數n對注漿殘余應力的影響Fig.3 Influence of rheological index on residual stress

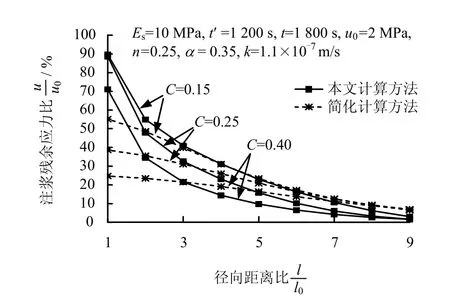
圖4 稠度系數C對注漿殘余應力的影響Fig.4 Influence of consistency index on residual stress

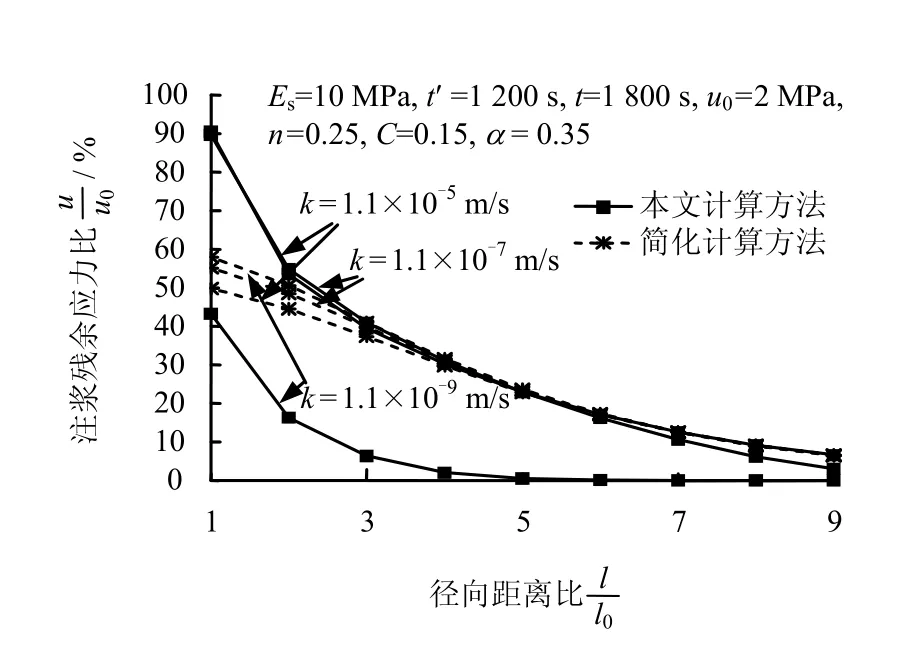
圖5 滲透系數k對注漿殘余應力的影響Fig.5 Influence of permeability coefficient on residual stress

由圖6可以看出，壓縮模量Es對注漿殘余應力也有較大的影響，兩種方法的計算結果都隨Es的增大而減少；徑向距離比為 1處，隨著Es從 1 MPa增加到100 MPa，本文算法計算結果從90.17%減小到 74.85%，而簡化算法結果則從 91.20%減小到12.60%。分析原因主要是土體壓縮模量的增加會造成注漿殘余應力消散的加快。同時還可以發現，壓縮模量對簡化算法的計算結果影響更大，而當Es=1 MPa時兩種方法計算結果較為接近。

圖6 壓縮模量Es對注漿殘余應力的影響Fig.6 Influence of compression modulus on residual stress

由圖 7可以看出，隨著注漿持續時間t′從1200 s增加到3600 s，兩種方法計算的注漿殘余應力結果都有所增大，但變化并不明顯，工程中注漿持續時間一般在20 min（1200 s）左右。

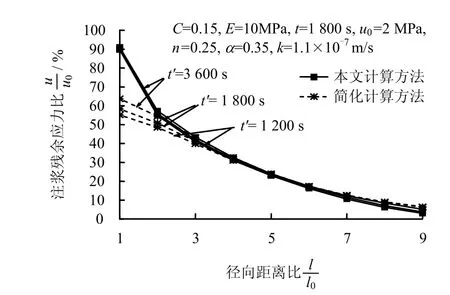
圖7 注漿持續時間 t′對注漿殘余應力的影響Fig.7 Influence of injection time on residual stress

由圖8可以看出，隨著固結時間t的增加，兩種算法計算的注漿殘余應力結果都迅速減少；徑向距離為1處，24 h（86400 s）后，簡化方法計算注漿殘余應力結果只有2.22%。

5 模型驗證

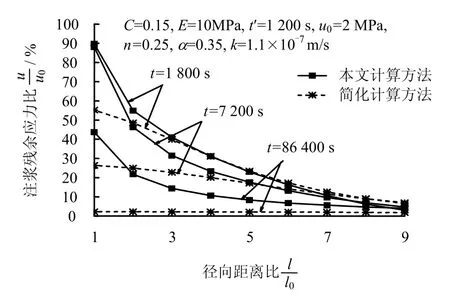
圖8 固結時間t對注漿殘余應力的影響Fig.8 Influence of consolidation time on residual stress

試驗場地為杭州市奧體博覽中心項目，該工程的場地土性質較差，分布著較厚的粉土與黏性土。試驗采用樁徑為800 mm的鉆孔灌注樁，樁長為39.2 m，成樁15 d后，將3.5 t水灰比為0.6的水泥漿通過注漿管注入樁端。注漿時，注漿泵輸出壓力約為1.0～1.5 MPa；注漿結束后，樁端附加壓力逐漸消散：注漿剛結束時，樁端附加壓力為 0.678 MPa；經過30 min，樁端附加壓力為0.251 MPa；經過90 min，樁端附加壓力為0.169 MPa；經過24 h，樁端附加壓力為0.067 MPa。

對比簡化方法與本文方法，計算注漿殘余應力結果如表1所示，其中主要參數取值如下：注漿持續時間t′取 1200 s，α=0.35，土體Es=35 MPa，k=1.1×10-5m/s，稠度系數C=0.15，n=0.25，詳細的試驗情況及注漿參數見鄒健等[3]的研究。

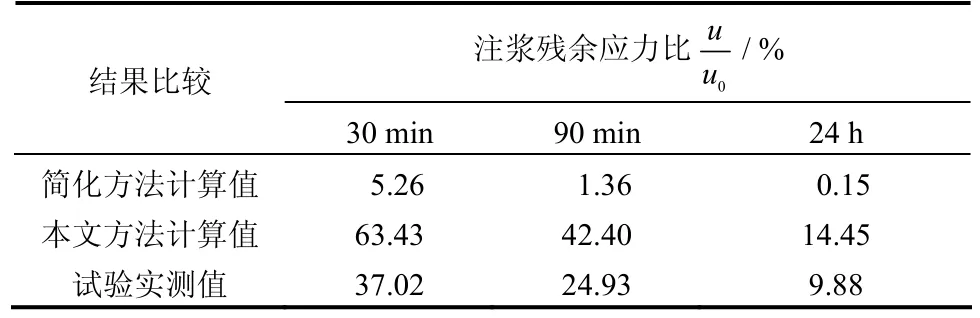
表1 注漿殘余應力計算與實測結果比較Table1 Comparison of residual stresses between calculation and measurement

從表1中可以看出，通過簡化方法計算所得注漿殘余應力擴散過快，結果偏小，基本上沒有反映出真實的消散情況，30 min時5%的結果基本上可以忽略。而本文的方法雖然得到的結果偏大，但總體上能夠對殘余應力消散的變化趨勢作出較好的模擬，且偏于保守，鑒于后注漿過程中存在著很大的不確定性，該精度的結果可達到預測的要求。

6 結 論

（1）基于球形空腔擴張及一維徑向固結理論，對注漿樁的樁端注漿殘余應力進行理論研究，在負指數衰減的初始超孔隙壓力分布基礎上，得到了殘余應力隨時間及擴散半徑消散的解析解。

（2）在不考慮注漿擴散半徑的前提下，對該解析解進行了簡化，與本文的計算方法相比較，對模型主要影響因素參數分析發現，流變指數、稠度系數、土體的壓縮模量及固結時間是影響注漿殘余應力的關鍵因素，注漿殘余應力一般會隨著流變指數、稠度系數、土體的壓縮模量或固結時間的增大而減小。

（3）用本文方法計算注漿殘余應力的結果總體上能夠對殘余應力消散的變化趨勢作出較好的模擬，證明了該計算模型的可靠性。

[1]張忠苗. 灌注樁后注漿技術及工程應用[M]. 北京: 中國建筑工業出版社,2009.

[2]張忠苗,張乾青. 后注漿抗壓樁受力性狀的試驗研究[J].巖石力學與工程學報,2009,28(3): 475－482.ZHANG Zhong-miao,ZHANG Qian-qing. Experimental study on mechanical properties of post-grouting compressive pile[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(3): 475－482.

[3]鄒健,張忠苗,林存剛. 樁端后注漿樁殘余應力研究[J].巖石力學與工程學報,2011,30(增刊1): 3275－3280.ZOU Jian,ZHANG Zhong-miao,LIN Cun-gang.Analysis of residual stress on post grouted drilled shaft[J].Chinese Journal of Geotechnical Engineering,2011,30(Supp.1): 3275－3280.

[4]劉利民,李增選. 殘余應力及其對樁承載性狀的影響[J].特種結構,2000,17(4): 16－18.LIU Li-min,LI Zeng-xuan. Residual pile stress and its influence to pile bearing capacity[J]. Special structures,2000,17(4): 16－18.

[5]印長俊,王星華,馬石城. 灌注樁殘余應變的產生機制分析[J]. 工程力學,2009,26(7): 125－133.YIN Chang-jun,WANG Xing-hua,MA Shi-cheng.Analysis of generating mechanism of residual strain in cast-in-place piles[J]. Engineering Mechanics,2009,26(7): 125－133.

[6]張忠苗,張廣興,吳慶勇,等. 鉆孔樁泥皮土與樁間土性狀試驗研究[J]. 巖土工程學報,2006,28(6): 695－699.ZHANG Zhong-miao,ZHANG Guang-xing,WU Qing-yong,et al. Studies of characteristics of mudcake and soil between bored piles[J]. Chinese Journal of Geotechnical Engineering,2006,28(6): 695－699.

[7]袁敬強,陳衛忠,譚賢君,等. 軟弱地層注漿的細觀力學模擬研究[J]. 巖土力學,2011,32(增刊2): 653－659.YUAN Jing-qiang,CHEN Wei-zhong,TAN Xian-jun,et al.Mesomechanical simulation of grouting in weak strata[J].Rock and Soil Mechanics,2011,32(Supp.2): 653－659.

[8]劉俊偉,俞峰,張忠苗,等. 基于能量守恒的預制樁施工殘余應力模擬[J]. 巖土力學,2012,33(4): 1227－1232.LIU Jun-wei,YU Feng,ZHANG Zhong-miao,et al.Simulation of post-installation residual stress in preformed piles based on energy conservation[J]. Rock and Soil Mechanics,2012,33(4): 1227－1232.

[9]VESIC A S. Expansion of cavities in infinite soil mass[J].Soil Mechanics and Foundations Division，Proceedings of ASCE,1972,98(SM3): 265－290.

[10]朱小林,唐世棟. 利用孔隙水壓力-靜力觸探探頭估算軟黏土固結系數的理論分析[J]. 工程勘察,1986,(6): 8－12.ZHU Xiao-lin,TANG Shi-dong. Theoretic analysis of the estimation of consolidation coefficient by piezocone tests[J]. Geotechnical Investigation and Surveying,1986,(6): 8－12.

[11]張雁,劉金波. 樁基手冊[M]. 北京: 中國建筑工業出版社,2009.

[12]阮文軍. 基于漿液黏度時變性的巖體裂隙注漿擴散模型[J]. 巖石力學與工程學報,2005,24(15): 2709－2714.RUAN Wen-jun. Spreading model of grouting in rock mass fissures based on time-dependent behavior of viscosity of cement-based grouts[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(15): 2709－2714.

[13]楊秀竹,雷金山,夏力農,等. 冪律型漿液擴散半徑研究[J]. 巖土力學,2005,24(增刊2): 5862－5867.YANG Xiu-zhu,LEI Jin-shan,XIA Li-nong,et al. Study of grouting diffusion radius of exponential fluids[J]. Rock and Soil Mechanics,2005,24(Supp.2): 5862－5867.