基于達維堅科夫骨架曲線的軟土非線性動力本構模型研究

張如林，樓夢麟

（1.同濟大學 土木工程防災國家重點實驗室，上海 200092；2.中國石油大學（華東） 儲運與建筑工程學院，山東 青島 266555）

1 引 言

土的動力非線性本構關系是表征土體動力特性的最基本關系，是土動力學研究的核心問題之一，同時也是巖土工程領域研究的熱點和難點。模型建立得合理與否，對于重要工程場地的非線性地震反應，以及對于土工建筑及地基的動力響應機制的研究都是至關重要的。室內試驗和現場觀測均表明，土體的動力性質非常復雜，在循環荷載作用下，巖土材料的動應力-應變關系主要表現出非線性、滯后性和變形累積三方面的特征。在求解巖土體的地震反應問題時，需要考慮巖土體在動力作用下的非線性特征，就必然要涉及到巖土體的動力本構模型的選擇問題[1]。

土體動力非線性本構模型研究主要分 3類方法：①工程中常用的等效線性化方法[2]，該方法形式直觀簡單，是試驗結果的歸納，而且積累了大量工程經驗，在目前土體動力反應分析、場地非線性地震反應分析中應用廣泛，但它仍有不少缺點，如易產生“虛共振現象”，不能計算永久變形，在大應變、強震動時誤差大，把土的塑性耗能轉化為黏滯阻尼處理等等；②真非線性動力本構模型[3]，這類方法往往具有較多的模型參數，并且難以通過常規試驗獲得；③時域滯回非線性分析方法，該類方法包括Masing類、Iwan類以及多線性本構模型等，這也是本文研究所采用的方法。

試驗研究表明，飽和軟土的動剪切模量Gd與動剪應變γd之間的關系基本符合雙曲線關系[4]。Hardin等[5]提出了預測Gd與γd的經驗關系，即著名的Hardin-Drnevich模型，隨后Martin等[6]認為，達維堅科夫模型可以更好地描述軟土的動力變形特性。陳國興等[7]對達維堅科夫骨架曲線進行了一定的修正，并與南京及其鄰近地區土體試驗結果進行對比，獲得了達維堅科夫模型參數的擬合值。楊林德等[8]、劉齊建[9]曾對上海地區軟土的動力特性進行了研究，通過對試驗數據的擬合分析，發現對于上海典型飽和軟土、上海軟土的動力變形特性符合“應變軟化”規律，認為達維堅科夫模型能夠很好地描述Gd與γd、阻尼比D與γd之間的關系。

本文在前人研究成果基礎上，對軟土非線性動力本構關系進行了研究。基于Martin等[6]提出的達維堅科夫骨架曲線的土體動應力-應變關系，通過構造土體加載、再卸載的應力-應變關系滯回曲線，試圖建立一種更為適合上海地區軟土的非線性動力本構模型，從而為上海地區軟土場地的動力計算反應分析提供適用的動力本構模型。

2 達維堅科夫骨架曲線和動應力-應變滯回曲線表達式

巖土體一維動應力-應變關系的研究是巖土材料動力本構關系研究中最基本的內容。Masing[10]最早建立了等幅循環荷載作用下巖土體的一維動應力-應變關系，按下列規則來構造動本構關系：①土的動應力-應變關系的骨架曲線為雙曲線；②在初始加載過程中，動應力-應變關系遵循骨架曲線；③在初始反向卸載時土的動剪切模量與最大剪切模量相等，加、卸載應力-應變關系曲線與骨架曲線成2倍關系。上述規則被稱為Masing法則，本節首先從一維應力-應變關系骨架曲線開始推導。

2.1 達維堅科夫骨架曲線理論公式

Hardin等[5]提出，用一種雙曲線形式來描述土體的應力-應變關系，其動剪切模量比的表達式為

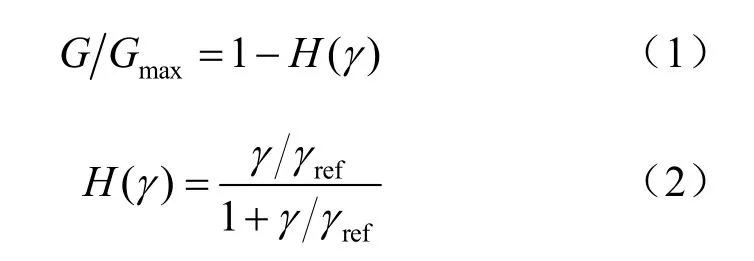
式中：G為剪切模量；Gmax為初始最大剪切模量；γ為剪應變幅值；γref=τfGmax，為參考剪應變，一般可取動剪切模量比為0.5所對應的剪應變幅值，如圖1所示。

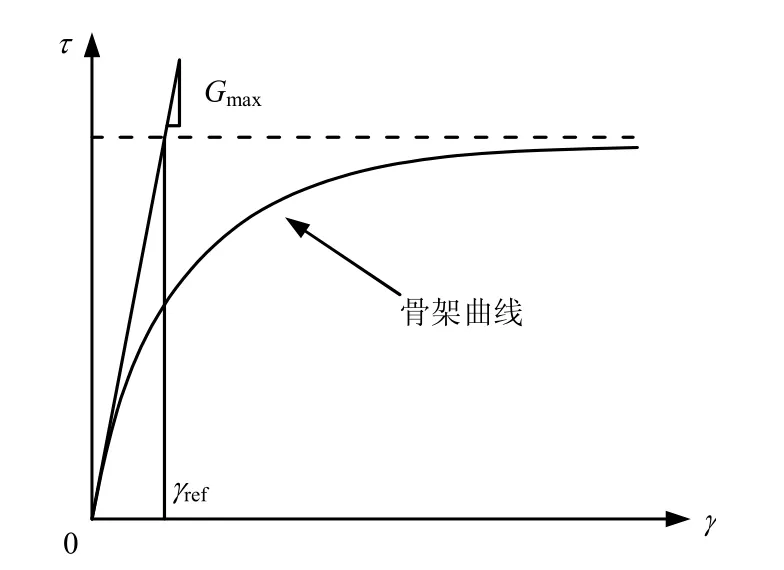
圖1 雙曲線應力-應變關系和參考剪應變示意Fig.1 Hyperbolic stress-strain curve and reference shear strain

Martin等[6]采用達維堅科夫骨架曲線來描述上述關系，將式（2）中的H(γ)改寫成如下形式：

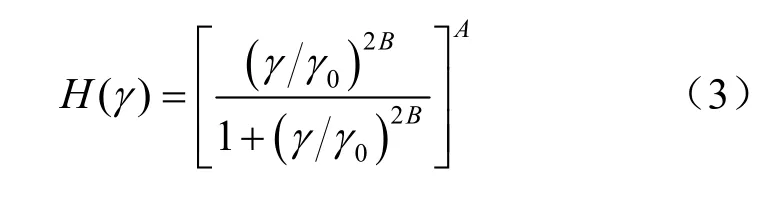
式中：A和B為與土性有關的擬合參數。需要指出的是，這里的γ0不再是具有明確物理意義的參考剪應變幅值，而僅僅是個擬合參數而已。顯然，當A=1.0，B=0.5，γ0=γref時，達維堅科夫模型描述的應力-應變關系曲線就退化為Masing雙曲線模型。

達維堅科夫模型應力-應變關系的骨架曲線可表示為

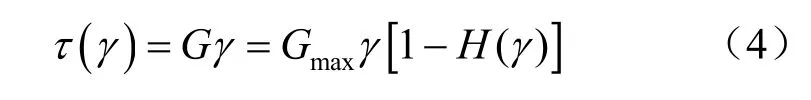
把式（3）代入到式（4），可得

2.2 骨架曲線增量剪切模量表達式

假定土體為理想黏彈性體，可從一般的模量衰減曲線得到歸一化的剪應力為

式中：Ms為模量衰減系數，是一個歸一化的割線模量。

通過對式（6）求γ的導數，可得到歸一化的切線模量Mt，本文將其稱為模量乘子，計算表達式如下：

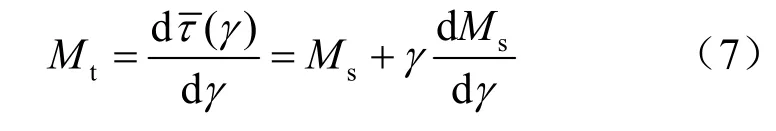
增量剪切模量G就可以表示為

再對式（5）求導，就可得到達維堅科夫骨架曲線中的增量剪切模量表達式：

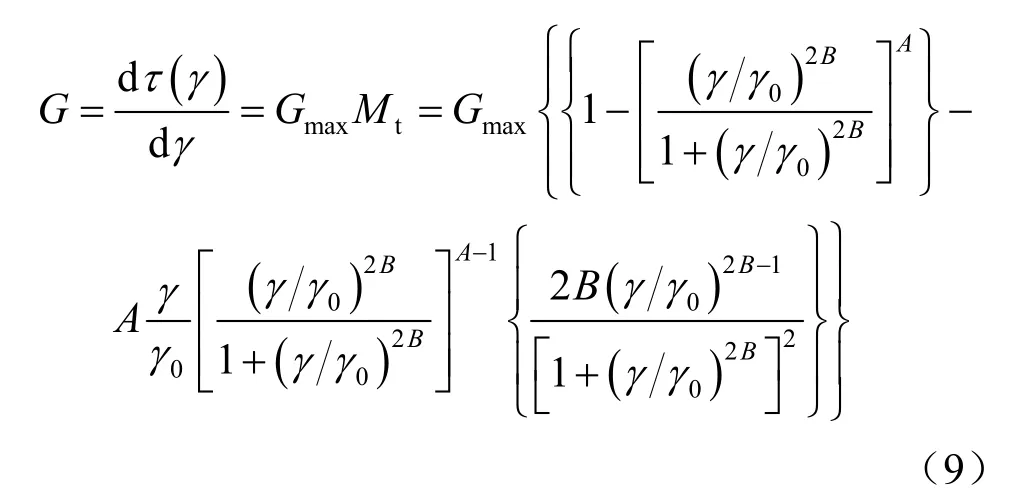
2.3 滯回曲線增量剪切模量表達式

當應力-應變關系的骨架曲線為達維堅科夫模型時，可采用Masing法則來構造相應的滯回曲線。根據Masing法則得到的滯回曲線的計算公式為

式中：τr為反轉點的應力；γr為反轉點的應變，如圖2所示。

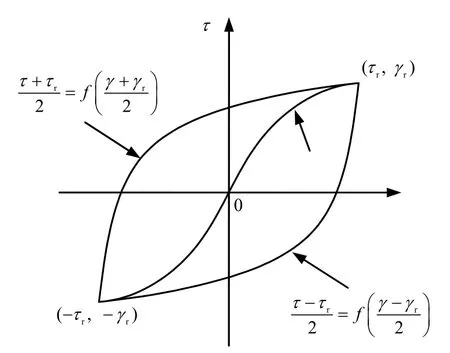
圖2 骨架曲線和滯回圈的構造Fig.2 Skeleton curve and stress-strain hysteresis curves

聯合式（10）和式（5）得到滯回曲線的計算表達式為

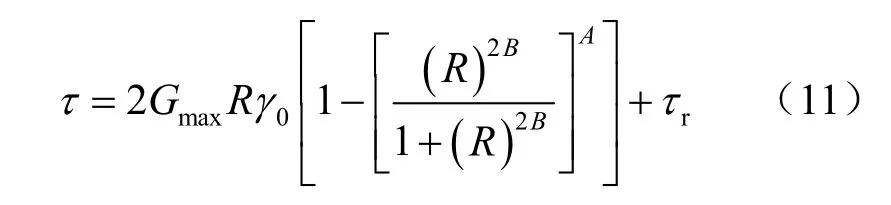
式中：R=(γ-γr)(2γ0)。

對式（11）求導，得出滯回曲線的增量剪切模量計算表達式為

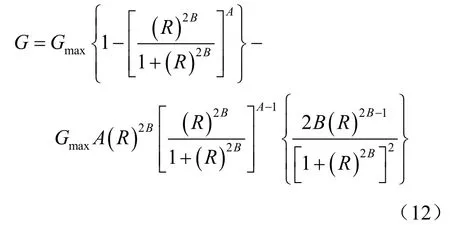
至此，就得到了完整的達維堅科夫骨架曲線和卸載、再加載的滯回曲線的表達形式。

3 程序編制與驗證

3.1 FLAC3D中本構模型的開發環境

本文在 FLAC3D提供的二次開發平臺上進行前面的本構模型程序的編制。FLAC3D采用面向對象的標準C++語言編寫而成，其所有的本構模型均以動態鏈接庫文件（.DLL）的形式提供給用戶，在計算過程中主程序會自動調用用戶指定的本構模型的動態鏈接庫文件[11]。FLAC3D自定義本構模型的主要功能是根據給出的應變增量得到新的應力。模型文件的編寫主要包括 5部分內容：①基類（class constitutive model）的描述；②成員函數的描述；③模型的注冊；④模型與FLAC3D之間的信息交換；⑤模型狀態指示器的描述。由于 FLAC3D自帶的本構模型和用戶自己編寫的本構模型繼承的都是同一個基類，因此，用戶自定義的本構模型和軟件自帶的本構模型的執行效率處于同一水平[11]。

對于本文來講，FLAC3D的本構模型開發工作主要是修改頭文件（.H文件）和程序文件（.CPP文件）。本文在線彈性本構模型（Userelas.H和Userelas.CPP兩個文件）的開放源代碼的基礎上進行修改。在線彈性本構模型中，加載和卸載、再加載過程中的模量值一直保持恒定不變，而本文模型在每次計算過程中，都要根據當前的應變狀態修改其模量值，來體現加載和卸載剪切模量的變化。

3.2 應變反轉與實現思路

多數材料在一維條件下的力學性質與三維條件下的力學性質存在很大差別，尤其是對于巖土這樣的顆粒破碎材料。在進行三維土層場地地震反應以及土與結構相互作用分析時，需要將前面的應力-應變關系從一維應變空間擴展到三維應變空間中。

在構建上述本構模型時，需要考慮應變反轉的問題。本文采用如下處理方式，對于三維分析問題，至少存在6個應變率張量分量，分別定義如下[12]：

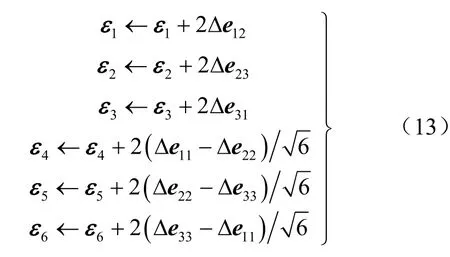
式中：Δeij為應變增量張量。

在應變空間中尋找應變軌跡的極值點，用上標0定義前一個點，用上標00定義前面第2個點，應變空間中前一個單位矢量的計算公式為

式中：下標i為1～6個分量。

新的應變增量 (εi-)在前一個單位矢量上的投影，或者用當前的偏移向量乘以就可以得到應變幅值：

將式（15）中的γ代入到式（7）中就可以得到模量乘子Mt，再代入到式（8）就可得到此時的剪切模量。

3.3 程序編制

Rosenblueth[13]、Newmark[14]等對 Masing 法則又做了2條補充規則：①若卸載應力-應變曲線或加載應力-應變曲線與骨架曲線相交，則偏離原曲線而遵循骨架曲線，稱為“上骨架曲線”規則；②若當前曲線與先前同方向的后繼應力-應變曲線相交，則當前曲線偏離原曲線，而遵循先前的后繼應力-應變關系曲線移動，稱“上大圈”規則。Masing法則和上述2條補充規則通常稱為“擴展的Masing法則”，如圖3所示。

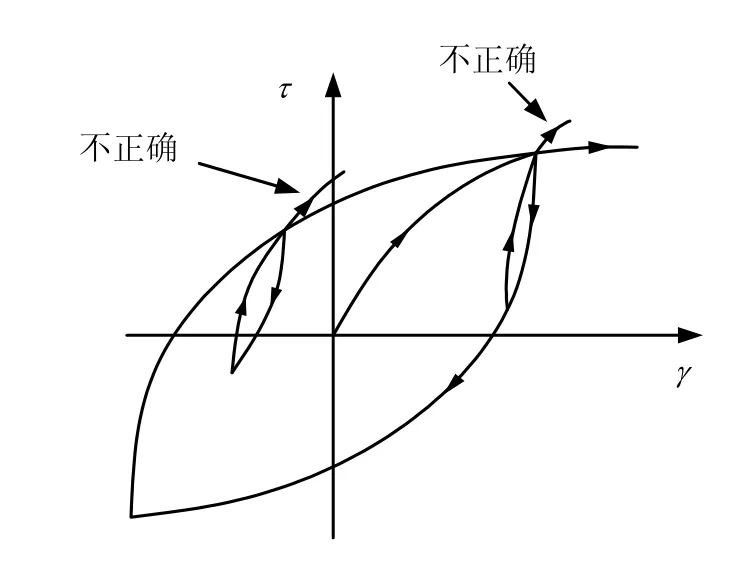
圖3 “上大圈”準則示意圖Fig.3 Sketch of up-large-cycle curve rule

擴展的 Masing法則難以用簡單的數學表達式描述，確定加、卸載的過程中應力-應變曲線的分支走向時只能采用數值判斷來實現，在程序編制時需要特別對拐點加以判斷。本文采用一種“棧”的數據結構形式，該數據結構采用“后進先出”的順序來對其中的數據進行操作[15]。在執行過程中，每遇到一個拐點，便將其狀態信息存入棧中（稱為入棧），一旦當前的應變水平達到或者超過棧中記錄的上次拐點的應變水平，就彈出記錄的該拐點的狀態信息（稱為彈棧），進而更新剪切模量乘子，這樣就可以簡便地實現復雜加載路徑下的應變轉折。

FLAC3D自帶一個Run()函數，該函數的主要作用是根據應變增量計算應力張量。本文在編制程序時，定義一個MyMt()函數來返回每個計算時刻的剪切模量值。在該函數中，首先提取Run()函數中的應變值，判斷此時是否為拐點，以及是否超過棧中記錄的上個拐點應變等操作，計算此時的模量乘子，進而更新模量值G并返回到Run()函數中，計算當前的應力值，如此重復這樣的步驟直到計算結束。整個程序計算流程圖如圖4所示。

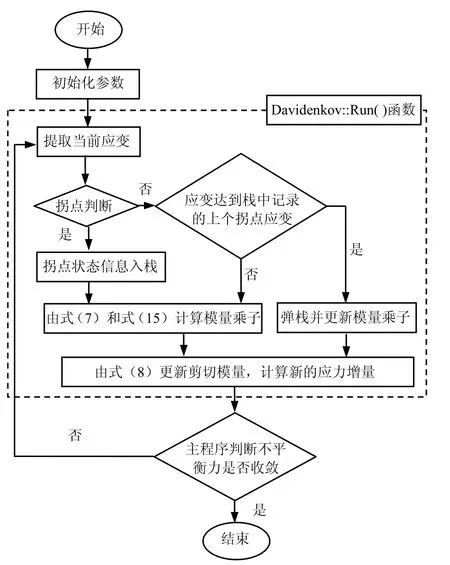
圖4 程序計算流程圖Fig.4 Flow chart of program

3.4 程序驗證

在程序驗證時，常采用一個單元進行計算，因為一個單元本身的應力和應變狀態簡單。為了驗證程序編制的可靠性，檢驗程序能否實現應變拐點判斷以及遵循廣義 Masing法則等功能，以一個單元（1 m×1 m×1 m）為例，通過施加剪應變的方式來研究復雜加載路徑下的應力-應變發展情況。剪應變加載路徑如圖5所示，計算得到的應力-應變關系發展曲線如圖6所示。

可以看出，在復雜加載路徑下，應變一旦遇到原來的拐點，仍會沿著原來的路徑繼續發展，當遇到骨架曲線，同樣也會沿著骨架曲線繼續前行，這說明本文編制的程序是合理可靠的。

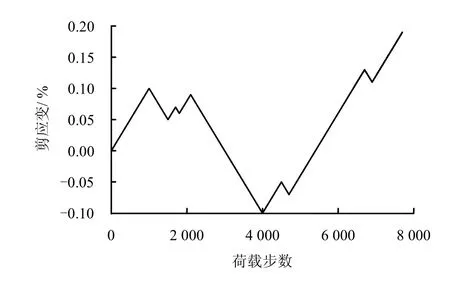
圖5 復雜加載路徑曲線Fig.5 Curve of complex loading path

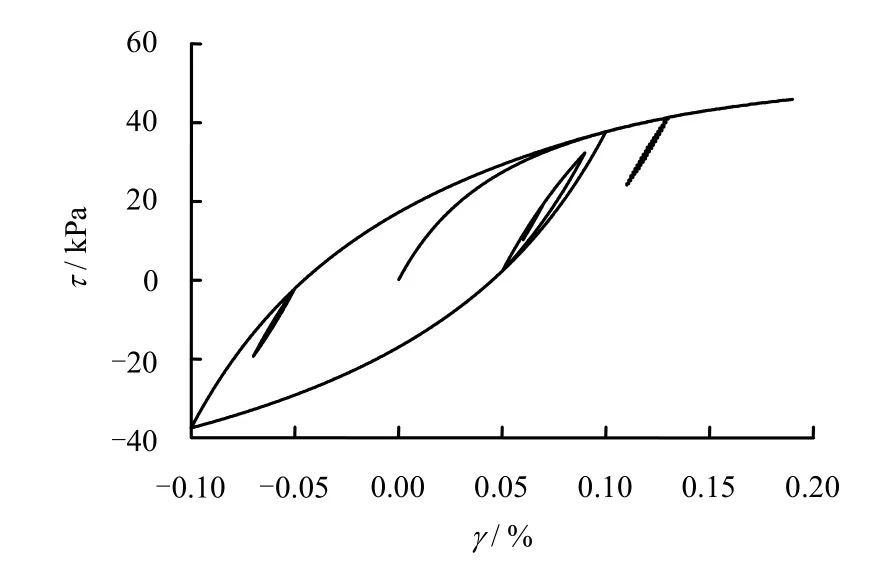
圖6 計算的應力-應變關系曲線Fig.6 Calculating stress-stress curve by program

4 土體試驗結果對比

4.1 相關文獻土體模型參數

楊林德[8]、劉齊建[9]等通過對上海市區典型軟土的動力試驗，測定了試樣的動剪切模量Gd、阻尼比D隨動剪應變γd變化的關系曲線。本文采用文獻[9]中粉質黏土典型土體試樣的動剪切模量比GGmax-γd和D-γd的實測曲線，所選土樣取自上海市軌道交通6號線德平路車站和明珠二期工程臨平路車站，共有14個土樣，其中德平路12個，臨平路2個。根據文獻[9]中試驗數據點擬合的達維堅科夫模型參數，以及本文通過插值，取GGmax=0.5所對應的剪應變幅值作為 Hardin-Drnevich模型中的參考剪應變γr。

將本文結果與文獻[16]中的土體試驗結果進行對比，通過最小二乘法擬合出文獻[16]中土體試樣的達維堅科夫模型參數，以及數據插值得到Hardin-Drnevich模型的參考剪應變γr。文獻[9]、[16]中兩種土體試樣的模型計算參數分別列于表1。

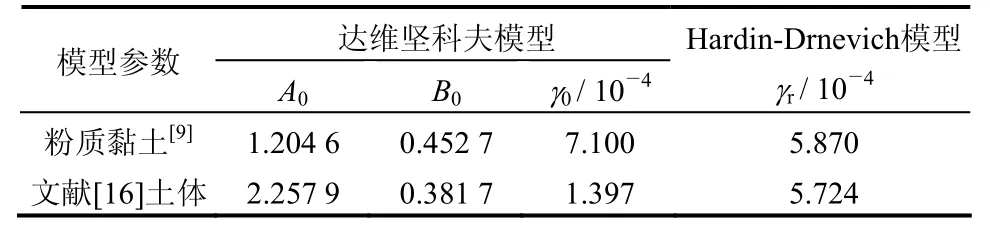
表1 兩種本構模型計算參數Table1 Calculation parameters of two constitutive models

4.2 結果對比分析

根據表1所列的兩種本構模型的計算參數，本文以一個單元（1 m×1 m×1 m）為例來進行計算分析。通過施加若干個水平的剪應變，得到不同剪應變幅值下動剪切模量比和阻尼比隨剪應變幅值的變化曲線，并與文獻[9]、[16]中的土樣試驗數據結果進行對比分析。對比結果如圖7～10所示。

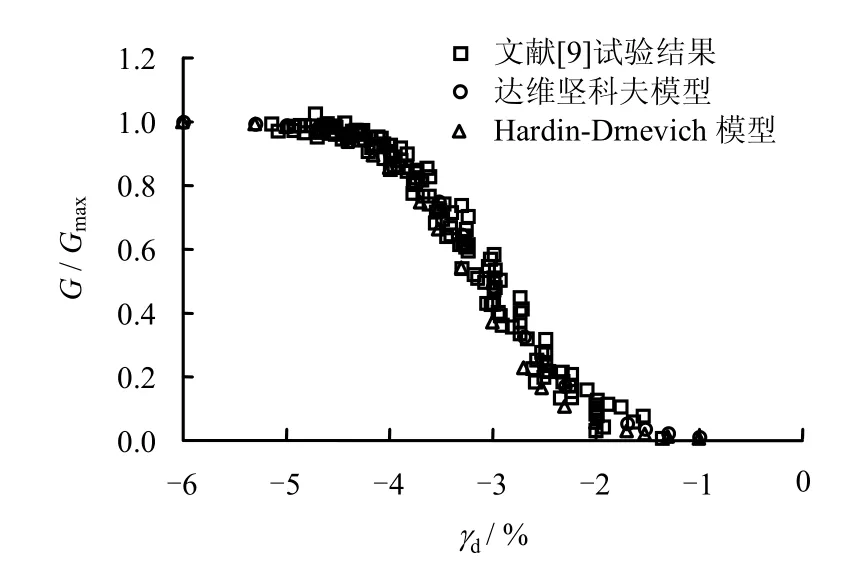
圖7 計算G/Gmax-γd曲線與文獻[9]試驗數據對比Fig.7 Comparisons of simulated G/Gmax-γdcurves and test data of Ref. [9]

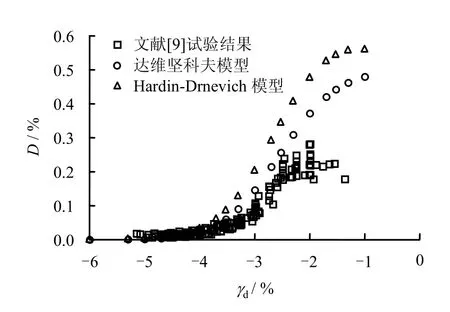
圖8 計算D-γd曲線與文獻[9]試驗數據對比Fig.8 Comparisons of simulated D-γdcurves and test data of Ref. [9]

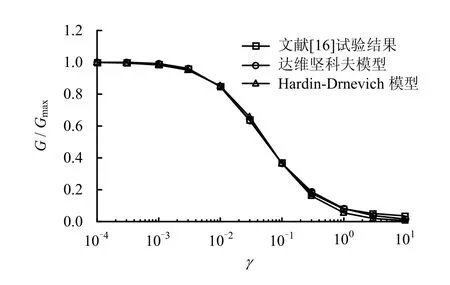
圖9 計算G/Gmax-γ 曲線與文獻[16]試驗曲線對比Fig.9 Comparisons of simulated G/Gmax-γ curves and test data of Ref. [16]

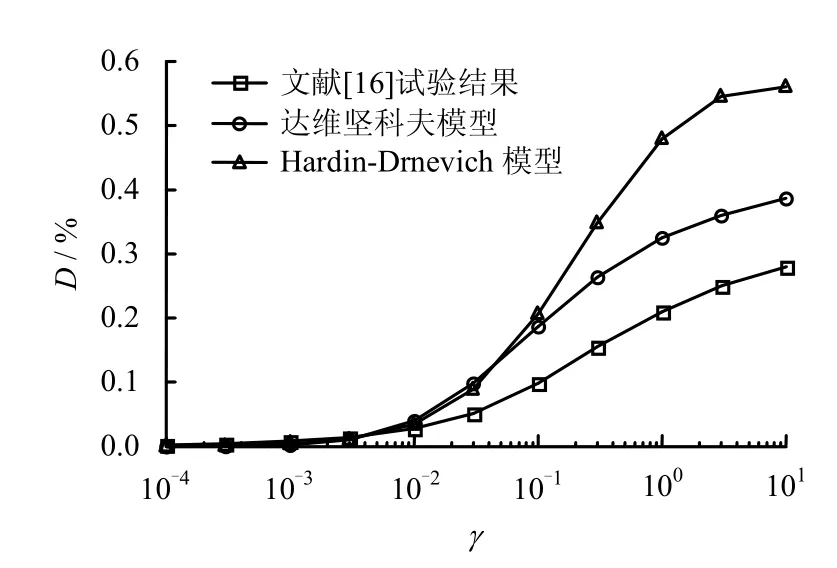
圖10 計算D-γ 曲線與文獻[16]試驗曲線對比Fig.10 Comparisons of simulated D-γ curves and test data of Ref. [16]

從圖7～10中本文計算結果與文獻[9]、[16]中的試驗數據結果對比來看，在整個計算剪應變范圍內，兩種本構模型計算的動剪切模量比隨剪應變幅值的變化曲線與試驗曲線都擬合較好。相比Hardin-Drnevich模型，采用達維堅科夫骨架曲線構造的滯回曲線模型可以更好地擬合試驗數據結果。在應變值小于 0.05%的范圍內，達維堅科夫本構模型擬合的阻尼比曲線較好；在應變值大于 0.05%時，雖然Hardin-Drnevich模型和達維堅科夫模型擬合阻尼比曲線都有一定的差距，但達維堅科夫模型的擬合效果仍然比Hardin-Drnevich模型要好得多。

研究表明[17]，實際土層場地地震反應分析中，土體的動剪應變幅值一般不會超過0.1%，因此，在大部分的動剪應變范圍內，采用達維堅科夫骨架曲線構造的非線性動力本構模型是可行的。從這個意義上來講，本文所構建的基于達維堅科夫骨架曲線的非線性動力本構模型比傳統的 Hardin-Drnevich模型要優越很多，也更適合上海地區軟土場地的動力計算分析。

5 結 論

（1）上海地區軟土的動力變形特性符合“應變軟化”規律，可以用達維堅科夫模型描述。

（2）以達維堅科夫骨架曲線為基礎，采用Masing法則，構造了土體加載、再卸載的動應力-應變關系滯回曲線，推導了骨架曲線和卸載、再加載滯回曲線的增量剪切剪切模量。

（3）將土體動應力-應變關系曲線從一維推廣到三維應變空間，基于FLAC3D提供的二次開發平臺，編制了基于達維堅科夫骨架曲線和符合廣義Masing法則的土體非線性動力本構模型計算程序，通過復雜加載路徑驗證了編制程序的正確性。

（4）研究結果表明，相比工程上廣泛應用的Hardin-Drnevich模型，基于達維堅科夫骨架曲線構造的本構模型所得到的軟土 G/Gmax-γd和D-γd曲線更符合試驗結果，驗證了本文所建立的本構模型的合理性，可用于上海地區軟土場地的動力計算反應分析。

（5）根據本文研究，在應變值超過 0.05%時，無論采用Hardin-Drnevich模型，還是達維堅科夫模型都會過高地估算阻尼比，由此而引起的計算誤差還需做深入的研究。另外，軟土動力特性十分復雜，影響軟土土體非線性的因素也很多，特別是孔隙水壓力效應、動態殘余應變及殘余應力特性、累積損傷及疲勞效應、震動軟化等，有必要在今后的研究中加以適當考慮。

[1]莊海洋,陳國興,梁艷仙,等. 土體動非線性黏彈性模型及其ABAQUS軟件的實現[J]. 巖土力學,2007,28(3):1267－1272.ZHUANG Hai-yang,CHEN Guo-xing,LIANG Yan-xian,et al. A developed dynamic viscoelastic constitutive relations of soil and implemented by ABAQUS software[J]. Rock and Soil Mechanics,2007,28(3):1267－1272.

[2]齊文浩,薄景山. 土層地震反應等效線性化方法綜述[J].世界地震工程,2007,23(4): 221－226.QI Wen-hao,BO Jing-shan. Summarization on equivalent linear method of seismic responses for soil layers[J].World Earthquake Engineering,2007,23(4): 221－226.

[3]WANG Z L,DAFALIAS Y F,SHEN C K. Bounding surface hypoplasticity model for sand[J]. Journal of Engineering Mechanics,ASCE,1990,116(5): 983－1001.

[4]HARDIN B O,RICHART F E. Elastic wave velocities in granular soils[J]. Journal of the Soil Mechanics and Foundations Division,ASCE,1963,89 (SM1): 33－65.

[5]HARDIN B O,DRNEVICH V P. Shear modulus and damping in soil: design equations and curves[J]. Journal of the Soil Mechanics and Foundation Engineering Division,ASCE,1972,98(7): 667－692.

[6]MARTIN P P,SEED H B. One dimensional dynamic ground response analysis[J]. Journal of Geotechnical Engineering,ASCE,1982,108(7): 935－954.

[7]陳國興,莊海洋. 基于 Davidenkov骨架曲線的土體動力本構關系及其參數研究[J]. 巖土工程學報,2005,27(8): 860－864.CHEN Guo-xing,ZHUANG Hai-yang. Developed nonlinear dynamic constitutive relations of soils based onDavidenkov skeleton curve[J]. Chinese Journal of Geotechnical Engineering,2005,27(8): 860－864.

[8]楊林德,陸忠良,白延輝,等. 上海地鐵車站抗震設計方法研究[R]. 上海: 同濟大學防災救災研究所,2002.

[9]劉齊建. 軟土地鐵建筑結構抗震設計計算理論的研究[博士學位論文D]. 上海: 同濟大學,2005.

[10]MASING G. Eigenspannungen und Verfestingung beim Messing[C]//Proceedings of the 2nd International Congress of Applied Mechanics. Zurich: [s.n.],1926: 332－335.

[11]陳育民,劉漢龍. 鄧肯-張本構模型在 FLAC3D中的開發與實現[J]. 巖土力學,2007,28(10): 2123－2126.CHEN Yu-min,LIU Han-long. Development and implementation of Duncan-Chang constitutive model in FLAC3D[J]. Rock and Soil Mechanics,2007,28(10):2123－2126.

[12]CUNDALL P A. A simple hysteretic damping formulation for dynamic continuum simulations[C]//Proceedings of the 4th International FLAC Symposium on Numerical Modeling in Geomechanics. Minneapolis: Itasca Consulting Group,2006.

[13]ROSENBLUETH E,HERREAR I. On a kind of hysteretic damping[J]. Journal of the Engineering Mechanics Division,ASCE,1964,90(4): 37－47.

[14]NEWMARK N M,ROSENBLUTH E A. Fundamentals of earthquake engineering[M]. Englewood Cliffs: Prentice Hall Inc.,1971: 163－192.

[15]朱戰立. 數據結構(C++語言描述)[M]. 北京: 高等教育出版社,2004.

[16]IDRISS I M,SUN J I. User's Manual for Shake91 Center for Geotechnical Modeling[D]. Davis: Department of Civil & Environmental Engineering,University of California,1992.

[17]CAMILO PHILLIPS,YOUSSEF M A. HASHASH.Damping formulation for nonlinear 1D site response analyses[J]. Soil Dynamics and Earthquake Engineering,2009,29(7): 1143－1158.